 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Ожидаемый риск актива и портфеля
Приобретая какой-либо актив, инвестор ориентируется не только на значение его ожидаемой доходности, но и на уровень его риска. Ожидаемая доходность выступает как некоторая величина, которую надеется получить инвестор, например 15%. Возможность получения данного результата подтверждается предыдущей динамикой доходности актива. Однако 15% – это только средняя величина. На практике доходность, которую получит инвестор, может оказаться как равной, так и отличной от 15%. Таким образом, риск инвестора состоит в том, что он может получить результат, отличный от ожидаемой доходности. Строго говоря, риск вкладчика заключается в том, что он получит худший, чем ожидаемый результат, т.е. его доходность составит менее 15%. Если фактическая доходность окажется больше 15%, то это плюс для инвестора. На практике в качестве меры риска используют показатели дисперсии и стандартного отклонения. Они показывают, в какой степени и с какой вероятностью фактическая доходность актива может отличаться от величины его ожидаемой доходности, то есть средней доходности. Данные параметры учитывают отклонения, как в сторону увеличения, так и уменьшения доходности по сравнению с ожидаемым значением. Как мы отметили выше, фактический риск состоит в том, что фактическая доходность окажется ниже ожидаемой, однако отмеченные параметры используются в качестве меры риска, в первую очередь, в силу простоты их определения. Ожидаемый риск портфеля представляет собой сочетание стандартных отклонений (дисперсий) входящих в него активов. Однако в отличие от ожидаемой доходности портфеля его риск не является обязательно средневзвешенной величиной стандартных отклонений (дисперсий) доходностей активов. Дело в том, что различные активы могут по-разному реагировать на изменение конъюнктуры рынка. В результате стандартные отклонения (дисперсии) доходности различных активов в ряде случаев будут гасить друг друга, что приведёт к снижению риска портфеля. Риск портфеля зависит от того, в каком направлении изменяются доходности входящих в него активов при изменении конъюнктуры рынка и в какой степени. Для определения степени взаимосвязи и направления изменения доходностей двух активов используют такие показатели как ковариация и коэффициент корреляции. Показатель ковариации определяется по формуле
где:
rA – доходность актива А в i-м периоде; rB – доходность актива В в i-м периоде; п – число периодов, за которые регистрировалась доходность активов. (Так как в нашем примере небольшое количество наблюдений, то в знаменателе вместо п – 1 берём значение п). Положительное значение ковариации говорит о том, что доходности активов изменяются в одном направлении, отрицательное – в обратном. Нулевое значение ковариации означает, что взаимосвязь между доходностями активов отсутствует. В табл. 8.2 приведены данные о доходности бумаг А ( Таблица 8.2. Расчёт ковариации и корреляции доходности бумаг А и В
(Так как в нашем примере небольшое количество наблюдений, то в знаменателе вместо п – 1 берём значение п).
Другим показателем степени взаимосвязи изменения доходностей двух активов служит коэффициент корреляции. Он рассчитывается по формуле
где: СоrrA,B – коэффициент корреляции доходности активов А и В; Сov A,B – ковариация доходности активов А и В; σA – стандартное отклонение доходности актива А; σB – стандартное отклонение доходности актива В. В нашем примере коэффициент корреляции равен:
Коэффициент корреляции изменяется в пределах от -1 до +1. Положительное значение коэффициента говорит о том, что доходности активов изменяются в одном направлении при изменении конъюнктуры, отрицательное – в противоположном. При нулевом значении коэффициента корреляция между доходностями активов отсутствует. |
= 
(8.8)
ковариация доходности активов А и В;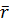
A – средняя доходность актива А за n периодов;
и В ( 
за четыре года. Определим ковариацию и вариацию доходности данных бумаг.
= 
= 
(8.9)