 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Доходность операций с облигациями
Тема 7. Математические основы расчёта эффективности операций с ценными бумагами 7.1. Дивиденды и проценты по ценным бумагам 7.2. Доходность операций с векселями 7.3. Доходность операций с облигациями 7.4. Доходность операций с акциями
Дивиденды и проценты по ценным бумагам Вложения денежного капитала в различного вида ценные бумаги – важнейший элемент развивающейся рыночной экономики. Цель финансовых вложений – получение дохода и/или сохранение капитала от обесценения в условиях инфляции. Следовательно, необходимо уметь правильно оценивать реальный доход по ценным бумагам. В зависимости от формы предоставления капитала и способа выплаты дохода ценные бумаги делятся на долговые и долевые. Долговые ценные бумаги(купонные облигации, сертификаты, векселя) обычно имеют фиксированную процентную ставку и являются обязательством выплатить полную сумму долга с процентами на определённую дату в будущем; по дисконтным облигациям доход представляет собой скидку с номинала. Долевые ценные бумаги(акции) представляют собой непосредственную долю держателя в реальной собственности и обеспечивают получение дивиденда в неограниченное время. Все прочие виды ценных бумаг являются производными от долговых либо долевых ценных бумаг и закрепляют право владельца на покупку или продажу акций и долговых обязательств. Это опционы, фьючерсные контракты и др. Расчёт дохода по различным видам ценных бумаг производится на основе полученных в предыдущих параграфах формул. Приведём несколько примеров. Пример 7.1 Депозитный сертификат номиналом 200 тыс.руб. (Р=200 тыс.руб.) выдан 14 мая с погашением 8 декабря под 18% годовых (i=0,18). Определить сумму погашения долгового обязательства (S) и дохода при начислении точных процентов (D). Решение 1. Находим точное число дней займа (17 дней мая + 30 дней июня + 31день июля + 31 день августа + 30 дней сентября + 31 день октября + 30 дней ноября + 8 дней декабря = 208 дней). 2. Сумма погашения долгового обязательства составит: S=P (1+ i∙ 3. Доход по депозитному сертификату составит: D = S – P = 220,52 – 200,0 = 20,52 тыс.руб. Ответ:при начислении точных процентов сумма погашения долгового обязательства составит 220,52 тыс.руб., а сумма дохода – 20,52 руб. Пример 7.2 Платёжное обязательство (Р) выдано на три месяца (q=3) под 25% годовых (i=0,25) с погашением 20 млн.руб. (S=20 млн.руб.). Определить доход владельца (D) данного платёжного обязательства. Решение Сначала по формуле дисконтирования определим текущую стоимость платёжного обязательства:
Доход владельца составит: D = 20,0 – 18,824 = 1,176 млн.руб. Ответ: текущую стоимость платёжного обязательства составит 18,824 млн.руб., а доход владельца – 1,176 млн.руб.
Доходность операций с векселями При покупке (учёте) векселей и других денежных обязательств до наступления срока платежа используются учётные ставки. Тогда доход, начисленный по учётной ставке (дисконт), становится доходом лица, купившего вексель, когда наступает срок оплаты. Владелец векселя получает указанную в нем сумму за вычетом дисконта, но зато раньше срока. Пример 7.3 Вексель выдан на сумму 10 млн.руб.(S=10 млн.руб.) со сроком оплаты 21 июля (К = 365). Владелец векселя учёл его в банке 5 июля по учётной ставке 20% (d=0.2). Определить сумму, полученную по векселю (S) и доход банка (D). Решение Срок от даты учёта до даты погашения составляет 21 – 5 = 16 дней. Сумма, полученная по векселю, составит: P = S(1- По формуле D =10 – 9,912 = 0,088 млн.руб. Ответ: сумму, полученная по векселю составит 9,912 млн.руб., а доход банка – 0,088 млн.руб.
Доходность операций с облигациями При операциях с облигациями источником дохода являются фиксированные проценты (в случае купонных облигаций), а также разность между ценой, по которой облигация приобретается, и ценой, по которой она выкупается. Выкупная цена облигации обычно совпадает с ее номиналом. Существуют облигации без выплаты процентов (дисконтные облигации), инвестирование средств в которые будет доходным только при покупке их со скидкой с номинала, т. е. с дисконтом. Введём обозначения: N – номинальная стоимость облигации; Ро – цена покупки облигации; I0 – доход по облигации; n – период, за который начисляются проценты; i – процентная ставка; ic – эффективная ставка сложных процентов. При расчётах дохода используют понятие курса облигации(Рk )
Тогда Подставляя в эту формулу выражение (7.1), получим
Пример 7.4 Облигация номиналом 10 000 руб., выпущенная на пять лет, приобретена по курсу 120. Рассчитать доход по облигации, если на неё ежегодно начисляются сложные проценты по ставке 18% ( Решение Расчёт дохода по облигации производится по формуле (7.3): 10 000 (2,2878 – 1,2) = 10000 ∙ 1,0878 = 10 878 (руб.). Ответ:доход по облигации составит 10 878 руб. |
;
= 
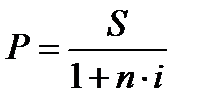млн.руб.
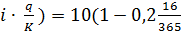) = 10 ∙ 0,9912 = 9,912 млн.руб.
получаем доход банка
(7.1)
(7.2)
(7.3)
.
= 10 000 [(1 + 0,18)5 – 
] =