 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Свойства криволинейного интеграла второго рода
Свойства криволинейного интеграла первого рода Криволинейный интеграл I рода обладает следующими свойствами:
1. Интеграл не зависит от ориентации кривой;
2. Пусть кривая C1 начинается в точке A и заканчивается в точке B, а кривая C2 начинается в точкеB и заканчивается в точке D (рисунок 2). Тогда их объединением будет называться криваяC1 U C2, которая проходит от A к B вдоль кривой C1 и затем от B к D вдоль кривой C2. Для криволинейных интегралов первого рода справедливо соотношение
3. Если гладкая кривая C задана параметрически соотношением
4. Если C является гладкой кривой в плоскости Oxy, заданной уравнением
5. Если гладкая кривая C в плоскости Oxy определена уравнением
6. В полярных координатах интеграл
где кривая C задана в полярных координатах функцией |
БИЛЕТ№44
Вычисление криволинейного интеграла первого рода
Пусть  — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция
— гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция  определена и интегрируема вдоль кривой
определена и интегрируема вдоль кривой  в смысле криволинейного интеграла первого рода. Тогда
в смысле криволинейного интеграла первого рода. Тогда
 .
.
Здесь точкой обозначена производная по  :
:  .
.
БИЛЕТ45
Механические приложения
· Работа A по перемещению материальной точки вдоль кривой l под воздействием силы  вычисляется по формуле
вычисляется по формуле

· Масса m кривой l, линейная плотность которой вдоль кривой l равна μ(x, y, z), выражается интегралом

· Координаты (xc, yc, zc) центра масс (центра тяжести) кривой l с линейной плотностью μ(x, y, z) находятся по формулам:
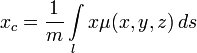 ,
,
 ,
,
 ,
,
где m — масса кривой l
· Моменты инерции кривой l относительно координатных осей:
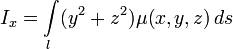 ,
,
 ,
,

· Сила притяжения точечной массы материальной кривой l есть
 ,
,
где μ(z, y, z) — линейная плотность кривой l, m0 — масса точки с координатами (x0, y0, z0); γ — постоянная тяготения,

| БИЛЕТ№46 Криволинейные интегралы второго рода | ||||||
Определение Предположим, что кривая C задана векторной функцией  , где переменная s − длина дуги кривой. Тогда производная векторной функции , где переменная s − длина дуги кривой. Тогда производная векторной функции 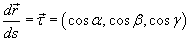 представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок 1). В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осейOx, Oy и Oz, соответственно. представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок 1). В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осейOx, Oy и Oz, соответственно.
Введем векторную функцию
существовал криволинейный интеграл
Таким образом, по определению,
где
где
|
Свойства криволинейного интеграла второго рода
Криволинейный интеграл II рода обладает следующими свойствами:
1. Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через−Cкривую противоположного направления - от B к A. Тогда
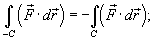
2. Если C − объединение кривых C1 и C2 (рисунок 2 выше), то

3. Если кривая C задана параметрически в виде  , то
, то

4. Если кривая C лежит в плоскости Oxy и задана уравнением  (предполагается, чтоR =0и t = x), то последняя формула записывается в виде
(предполагается, чтоR =0и t = x), то последняя формула записывается в виде





 и скалярная функцияF непрерывна на кривой C, то
и скалярная функцияF непрерывна на кривой C, то
 , то
, то
 , то
, то
 выражается формулой
выражается формулой
 .
.

 , определенную на кривой C, так, чтобы для скалярной функции
, определенную на кривой C, так, чтобы для скалярной функции
 . Такой интеграл
. Такой интеграл  вдоль кривой C и обозначается как
вдоль кривой C и обозначается как

 − единичный вектор касательной к кривой C.
− единичный вектор касательной к кривой C.
 .
.
 ,
, ,
, .
. единичный вектор касательной к кривой
единичный вектор касательной к кривой 

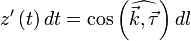
 с непрерывными частными производными первого порядка
с непрерывными частными производными первого порядка  . Тогда справедлива формула Грина
. Тогда справедлива формула Грина  где символ
где символ  указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки. Если
указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки. Если  , то формула Грина принимает вид
, то формула Грина принимает вид  где S − это площадь области R, ограниченной контуром C. Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией
где S − это площадь области R, ограниченной контуром C. Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией  Ротором или вихрем векторного поля
Ротором или вихрем векторного поля  называется вектор, обозначаемый
называется вектор, обозначаемый  или
или  и равный
и равный  Формула Грина в векторной форме записывается в виде
Формула Грина в векторной форме записывается в виде  Заметим, что формула Грина вытекает из "теоремы Стокса" при переходе от трехмерного случая к случаю двух координат.
Заметим, что формула Грина вытекает из "теоремы Стокса" при переходе от трехмерного случая к случаю двух координат.