ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Г.14 Здания с коническими круговыми покрытиями

Предыдущая 1 2 3 4 5 6 7 8 91011 12 13 Следующая

Для зданий с коническими круговыми покрытиями (рисунок Г.17) коэффициент m₁ определяется по таблице Г.3. Промежуточные значения определяются линейной интерполяцией.

Таблица Г.3

Уклон покрытия a, град.	m₁
a £ 30°
a ³ 60°

Для пологих куполов при a£ 7° следует учитывать только вариант 1.

Для менее пологих куполов при 7° < a £ 30° для варианта 2 следует принимать

m₂ = C_r2 (z/r)sinb,

где

При 30°< a < 60° для варианта 2 следует принимать:

m₂ = C_r2 (z/r)sinb; C_r2 = 1,7´30°/a.

Рисунок Г.17

Приложение Д
(обязательное)

Ветровые нагрузки

Д.1 Аэродинамические коэффициенты

Д.1.1 Отдельностоящие плоские сплошные конструкции

Отдельностоящие плоские сплошные конструкции на земле (стены, заборы и т.д.)

Для различных участков конструкций (рисунок Д.1) коэффициент с_х определяется по таблице Д.1;

z_e = h.

Рисунок Д.1

Таблица Д.1

Участки плоских сплошных конструкций на земле (см. рисунок Д.1)
А	В	С	D
2,1	1,8	1,4	1,2

Рекламные щиты

Для рекламных щитов, поднятых над землей на высоту не менее d/4 (рисунок Д.2):

с_х = 2,5k_l, где k_l - определено в Д.1.15.

Рисунок Д.2

Равнодействующую нагрузку, направленную по нормали к плоскости щита, следует прикладывать на высоте его геометрического центра с эксцентриситетом в горизонтальном направлении е = ± 0,25b.

z_e = z_g + d/2.

Д.1.2 Прямоугольные в плане здания с двускатными покрытиями

Вертикальные стены прямоугольных в плане зданий

Таблица Д.2

Боковые стены	Наветренная стена	Подветренная стена
Участки
А	В	С	D	Е
-1,0	-0,8	-0,5	0,8	-0,5

Для наветренных, подветренных и различных участков боковых стен (рисунок Д.3) аэродинамические коэффициенты с_е приведены в таблице Д.2.

Для боковых стен с выступающими лоджиями аэродинамический коэффициент трения с_f = 0,1.

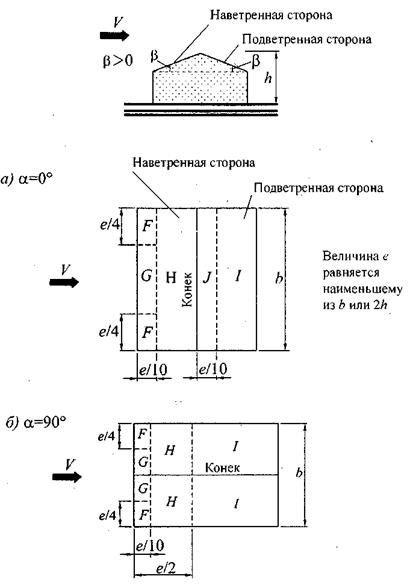
Рисунок Д.3

Двускатные покрытия

Для различных участков покрытия (рисунок Д.4) коэффициент с_е определяется по таблицам Д.3,а и Д.3,б в зависимости от направления средней скорости ветра.

Для углов 15° £ b £ 30° при a = 0° необходимо рассмотреть два варианта распределения расчетной ветровой нагрузки.

Для протяженных гладких покрытий при a = 90° (рисунок Д.4,б) аэродинамические коэффициенты трения с_е = 0,02.

Рисунок Д.4

Таблица Д.3а

a = 0°

Уклон b	F	G	Н	I	J
15°	-0,9	-0,8	-0,3	-0,4	-1,0
0,2	0,2	0,2
30°	-0,5	-0,5	-0,2	-0,4	-0,5
0,7	0,7	0,4
45°	0,7	0,7	0,6	-0,2	-0,3
60°	0,7	0,7	0,7	-0,2	-0,3
75°	0,8	0,8	0,8	-0,2	-0,3

Таблица Д.3б

a = 90°

Уклон b	F	G	Н	I
0°	-1,8	-1,3	-0,7	-0,5
15°	-1,3	-1,3	-0,6	-0,5
30°	-1,1	-1,4	-0,8	-0,5
45°	-1,1	-1,4	-0,9	-0,5
60°	-1,1	-1,2	-0,8	-0,5
75°	-1,1	-1,2	-0,8	-0,5

Д.1.3 Прямоугольные в плане здания со сводчатыми и близкими к ним по очертанию покрытиями

Рисунок Д.5

Примечание - При 0,2 £ f/d £ 0,3 и h₁/l ³ 0,5 необходимо учитывать два значения коэффициента с_e₁.

Распределение аэродинамических коэффициентов по поверхности покрытия приведено на рисунке Д.5.

Аэродинамические коэффициенты для стен принимаются в соответствии с таблицей Д.2.

При определении эквивалентной высоты (11.1.5) и коэффициента v в соответствии с 11.1.1: h = h₁ +0,7f.

Д.1.4 Круглые в плане здания с купольными покрытиями

Значения коэффициентов с_е в точках А и С, атакже в сечении ВВ приведены на рисунке Д.6. Для промежуточных сечений коэффициенты с_е определяются линейной интерполяцией.

При определении эквивалентной высоты (11.1.5) и коэффициента v в соответствии с 11.1.1: h = h₁ +0,7f.

Рисунок Д.6

Предыдущая 1 2 3 4 5 6 7 8 91011 12 13 Следующая