 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Глава 9. Непараметрические критерии
Расчет средних величин и их сопоставление, как отмечалось в главах 7-8, строится на определении и использовании параметров вариационных рядов. Отсюда и название данного раздела статистики – параметрическая. Однако, в тех же главах указывалось, что параметры вариационных рядов можно определять лишь при соответствии их ряду требований. И одно из требований – нормальное (или близкое к нему) распределение вариантов по соответствующим частотам. Если распределение не нормальное, то для выявления связей между явлениями следует прибегать к непараметрическим методам. К преимуществам последних следует отнести то, что они могут использоваться и в случае нормального распределения и при оценке качественных признаков. Кроме того, использование многих непараметрических критериев не требует длительных и сложных расчетов, т.к. предполагает применение уже разработанных таблиц. Однако непараметрические критерии требуют очень четкой постановки задачи и использования их в строго очерченных для каждого метода границах.
9.1. Критерий
 на примерах. на примерах. Пример 1. В противотуберкулезном стационаре новый метод (НМ) лечения применялся у 42 пациентов, страдающих открытой формой туберкулеза: у 24 из них длительность лечения продолжалась до 6 месяцев, у 18 – свыше 6 месяцев; у 58 пациентов, применялся старый метод (СМ) лечения: у 16 из них лечение продолжалось до 6 мес., у 42 – свыше 6 месяцев. Вопрос: эффективен ли новый метод лечения больных туберкулезом? Представим данные задачи в таблице 9.1.1.
Таблица 9.1.1. Распределение больных с туберкулезом легких по длительности лечения и наличию БК в мокроте
Приведенная таблица называется таблицей "четырех полей" (или 2х2), т.к. вся основная информация содержится в четырех клетках, обозначенных буквами a, b, c, d. Значение критерия хи-квадрат рассчитывается в данном случае по следующей формуле.
где n – общее число наблюдений
Определено, что: Если Если Если Вывод: новый метод лечения более эффективен, чем старый (p<0,01).
Пример 2. В эндокринологическом диспансере при наличии нарушений углеводного обмена обследовано 1500 человек, в том числе 800 человек с факторами риска. Распределение обследованных по наличию факторов риска и уровню нарушения углеводного обмена приведено в таблице 9.1.2. Вопрос: влияют ли факторы риска на нарушение углеводного обмена?
Таблица 9.1.2. Распределение обследованных по уровню нарушений углеводного обмена и наличию факторов риска
Величина критерия
где n – общее число наблюдений; r – число градаций в результативном признаке s – число градаций в факторном признаке i – 1, 2, ….,r; j – 1, 2, …., s; nij – число, стоящее на пересечении строки i и графы j; ni - сумма по i-ой строке; nj – сумма по j-ой графе; На практике эта формула реализуется так:
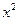 могут использоваться лишь для таблиц "2х2". В примере 2 информация о распределении обследованных представлена в виде таблицы "2х3", т.е. в одном из признаков градаций более двух. могут использоваться лишь для таблиц "2х2". В примере 2 информация о распределении обследованных представлена в виде таблицы "2х3", т.е. в одном из признаков градаций более двух. В общем виде таблицы, в которых хотя бы один признак имеет градации числом более двух, принято обозначать как таблицы "n x m", где n и m могут быть любыми числами и будут обозначать соответственно число градаций в одном и другом признаках. В таблицах "n x m" критические значения Первый – определяют так называемое число степеней свободы n1 = (n – m) (m – 1). В примере 2 n1 = (2 – 1) (3 – 1) = 2. Второй – по таблице 9.1.3 находят критические
Таблица 9.1.3 Критические значения
Вывод по примеру 2: факторы риска влияют на нарушение углеводного обмена (p<0,001). Однако здесь может возникнуть вопрос: а какая связь между факторами риска и нарушением углеводного обмена? Для определения силы связи между факторным и результативным признаком используются критерии Крамера (К).
К = n - число единиц наблюдения; Z – число градаций одного признака; S – число градаций другого признака. Первый признак в нашей задаче - факторы риска, имеет две градации: 2 – 1 =1, второй признак – нарушение углеводного обмена, имеет три градации: 3 – 1 = 2. Следовательно, число единиц наблюдения умножаем на 1. К = Если К<0,3, то связь сильная; Если К находится в пределах от 0,3 до 0,6 – связь средняя; Если К >0,6, то связь сильная. Вывод: между факторами риска и нарушением углеводного обмена связь сильная. Примечание: если в таблице с данными задачи хотя бы в одной клетке встречается число меньше 5, то вычисление
9.2. Точный метод Фишера (ТМФ) В случаях, когда в таблицах вида "n x m" встречаются числа, меньше 5 (до 0 включительно), расчет величины Однако могут возникать ситуации, когда даже в таблице "2х2" будут встречаться малые (от 0 до 4) числа. В этих случаях очень удобно использовать ТМФ. Заключается он в следующем. Выдвигается "нулевая гипотеза", в соответствии с которой влияние фактора на результат равно нулю. Затем с помощью ТМФ оценивается вероятность ошибочности этой гипотезы – РТМФ. Если РТМФ > 0,05, то вероятность ошибочности гипотезы велика и связь признается достоверной. Если РТМФ < 0,05 – гипотеза подтверждается и наличие связи между изучаемыми признаками отрицается. Рассчитывается РТМФ по формуле:
РТМФ =
где
n – общее число наблюдений ! – знак факториала, означающий необходимость последовательного перемножения чисел от 1 до обозначенного. Например, 5! = 1 × 2 × 3 × 4 × 5 = 120 7! = 1 × 2 × 3 × 4 × 5 × 6 × 7 = 5040 Принято считать 0! = 1 Рассмотрим ТМФ на примерах. Пример 1. В стационаре язвенную болезнь желудка первым способом лечили у 8 человек, осложнений ни у кого не наблюдалось. Вторым способом то же заболевание лечили у 12 человек, из них у двоих наблюдались осложнения. Вопрос: влияет ли способ лечения на частоту осложнений? Представим данные задачи в таблице 9.2.1.
Таблица 9.2.1. Распределение больных язвенной болезнью желудка, лечившихся различными способами по наличию или отсутствию осложнений
Вывод: нулевая гипотеза не подтверждается, связь есть. Следовательно, способ лечения влияет на частоту осложнений.
Пример 2. В стационаре острый инфаркт миокарда первым способом лечили у 11 человек, осложнений ни у кого не наблюдалось. Вторым способом то же заболевание лечили также у 11 человек, из них у 4 наблюдались осложнения. Вопрос: влияет ли способ лечения на частоту осложнений? Представим данные задачи в таблице 9.2.2.
Распределение больных острым инфарктом миокарда, лечившихся различными способами по наличию или отсутствию осложнений
Вывод: нулевая гипотеза подтверждается, связи нет. Следовательно, способ лечения не влияет на частоту осложнений. 9.3. Критерий знаков (КЗ). Применяется для выявления различий в средних тенденциях в связанных выборках, т.е. в выборках, в которых каждому наблюдению соответствует свой контроль (очень часто – исходный уровень какого-либо параметра и конечный, после проведения определенных мероприятий). Пример 1. Исследуется эффективность новой моющей добавки. Проведено 8 опытов, в 7 из них получено лучшее очищение, в 1 – худшее, чем без добавки. Необходимо установить, является ли улучшение очищения статистически достоверным или наблюдаемые изменения можно отнести к случайным колебаниям? Алгоритм определения КЗ: 1. Определить, какое изменение (состояние) будет обозначаться знаком (+) или (-). 2. Проставить знаки и подсчитать общее количество наблюдений (n0) и количество знаков, встречающееся меньшее количество раз (nм). 3. По таблице 9.3.1 определить, при каком максимальном числе менее часто встречающихся знаков различия можно считать существенными. 4. Сопоставить табличные данные с опытными и сделать вывод. Решение примера: 1. Обозначим знаком (+) каждый случай лучшей очистки при использовании новой моющей добавки. Знаком (-) – случай хорошей очистки. 2. В примере получается общее число наблюдений n0 = 8, количество менее часто встречающихся знаков nм = 1. 3. По таблице 9.3.1 находим, что при n0 = 8, nм = 1, т.е. если из 8 наблюдений в одном встретился отрицательный результат, а в 7 – положительный, можно с 95 – процентной уверенностью (р<0,05) утверждать, что получение лучшего эффекта в данном случае достоверно, не случайно.
Пример 2. В клинику поступило за месяц 27 больных с нарушениями мозгового кровообращения. Для их лечения использовали новый способ, который оказался в 21 случае более эффективным, а в 6 случаях – таким же эффективным, чем старый. Решение примера: 1. Обозначим знаком (+) случаи более эффективного лечения, знаком (-) – прочие. 2. Общее число наблюдений n0 = 27, nм = 6. 3. По таблице 9.3.1 находим, что при n0 = 27, nм = 8. В примере nм = 6, следовательно, с достоверностью, превышающей 95% (р<0,05) можно говорить о большей эффективности нового способа лечения.
Таблица 9.3.1. Определение максимального числа менее часто встречающихся знаков, при которых различия в парных сравнениях можно считать существенными (р<0,05).
9.4. Критерий Q Розенбаума (критерий "хвостов") Применяется для оценивания различий в средних тенденциях двух независимых выборок. Пример.
(13 человек) 9 9 10 10 10 11 11 11 11 11 12 12 12 Методика 2 (15 человек) 8 8 8 9 9 10 10 10 10 10 11 11 11 11 11 Определим: S1 – число наблюдений первого ряда, превышающих по своему значению максимальную величину второго ряда: S1 = 3; S2 – число наблюдений второго ряда, меньших, чем минимальная величина первого ряда: S2 = 3. Q = S1 + S2 = 3 + 3 =6 По таблице 9.4.1. находим, что при n1 = 13 и n2 = 15 минимальное значение Q, при котором различия в сравниваемых выборках можно считать существенными, равняется 6. В примере Q = 6, следовательно методика 2 в целом позволяет в более короткие сроки нормализовать состояние больных (р = 0,05). Ограничения и условия применения критерия Q 1. При числе наблюдений в каждой группе меньше 11 критерий Q не применяется. 2. При числе наблюдений от 11 до 26 используется таблица 2. Причем n1 и n2 должны быть если не равны, то очень близки, отличаясь лишь на несколько единиц. 3. При n1 и n2 больших, чем 26, различия в сравниваемых выборках считаются значимыми с р<0,05 при Q > 8, и с р<0,01 при Q > 11. При этом, если n1 и n2 не превышают 50, различия между ними должны быть в пределах 10 единиц; если n1 и n2 в границах от 51 до 100 – различия могут достигать 15 – 20 единиц; при n1 и n2 > 100 – различие между ними допустимы в 1,5 – 2 раза.
Минимальные значения Q, при которых различия между выборками можно считать значимыми (р<0,05)
|



 –
–  Длительность лечения
Длительность лечения
 =
= 
 = 8,9
= 8,9 3,84, то различия достоверны с (p<0,05);
3,84, то различия достоверны с (p<0,05);

 = 99,4
= 99,4
 = 0,26
= 0,26 ,
, Способы лечения
Способы лечения =
=  = 0,37
= 0,37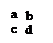 Способы лечения
Способы лечения = 0,04
= 0,04 Методика 1
Методика 1