ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Силовой расчет структурной группы
Кривошипно-ползунный механизм рабочей машины
Таблица 1
Н – ход ползуна
Кинематический анализ механизма В ходе кинематического анализа определяются кинематические характеристики звеньев механизма и точек звеньев. При решении задач кинематики методом планов расчет выполняется в три этапа: - разметка механизма; - расчет скоростей; - расчет ускорений. Познакомимся более подробнос методикой кинематического анализана примере кривошипно-ползунного механизма, основные параметры которого приведены в табл.1, вариант 6.
Разметка механизма Для определения скоростей и ускорений методом планов необходимо построить разметку механизма. Разметка – ряд последовательных положений механизма, охватывающих цикл его движения. Разметка выполняется методом засечек в масштабе. Обозначим масштабный коэффициент разметки как
где Длина отрезка ОА выбирается произвольно. Она должна быть такой, чтобы масштабный коэффициент Длины отрезков, АВ и
Разметка строится для 12 положений механизма. Ее построение начинается с выбора положения оси вращения кривошипа (на рис. 1.1 – точка О), и, в соответствии с исходными данными, изображается направляющая ползуна. В рассматриваемом примере ползун перемещается горизонтально. Его направляющая смещена относительно точки О на величину +е. В связи с этим, через точку О проводим горизонтальную прямую и параллельно ей на расстоянии В ходе разметки определяются крайние положения механизма. В этих положениях ползун меняет направление движения, т.е. скорость ползуна Соединим точки О и В*. Прямую ОВ* продолжим до пересечения с траекторией движения точки А (с окружностью). Получим точку А*. В этом положении кривошип изображается прямой ОА*, а шатун – прямой А*В*.
Рис. 1.1. План положений механизма
Для определения второго крайнего положения механизма соединим точки В** и О. Обозначим точку пересечения прямой ОВ** с траекторией движения точки А кривошипа, как А**. Отрезки ОА** и А**В** изображают кривошип и шатун во втором крайнем положении механизма. В первом крайнем положении А*ОВ* начинается рабочий ход механизма, а в положении ОА**В** рабочий ход заканчивается. В связи с этим, первое крайнее положение примем за нулевые (на рис. 1.1 точка А* совпадает с точкой А0, а точка В* - с точкой В0), а второе крайнее – за шестое. Соответственно точка А** совпадает с точкой А6, а точка В** - с точкой В6. Для построения промежуточных положений механизма разделим каждый из улов, образованных кривошипом в крайних его положениях, на шесть равных частей. Получим 10 промежуточных положений кривошипа (ОА1, ОА2, ... , ОА11). Нумерация положений производится в направлении вращения кривошипа. Для каждого из этих положений методом засечек определяются соответствующие положения точек В шатуна и ползуна. Так, например, для определения положения точки В1 надо из точки А1 сделать засечку на прямой В каждом положении механизма в соответствии с исходными данными определяются положения центров масс
Расчет скоростей
По заданному значению
Вектор скорости Шатун совершает плоское движения. Скорости его точек А и В связаны зависимостью [1-3]:
где Шатун в относительном движении вращается вокруг мгновенно неподвижной точки А. В связи с этим, вектор Уравнение (1.2) имеет два неизвестных и может быть решено. Графическое решение этого уравнения называется планом скоростей. Для построения плана скоростей надо выбрать масштабный коэффициент
где Длина отрезка Решим уравнение (1.2) для четвертого положения механизма. На свободном поле чертежа (рис. 1.2) выбираем точку Скорости
Рис. 1.2. План скоростей
Из этой пропорции следует Отрезок Для определения скорости
Отрезок Расчет модулей скоростей в рассматриваемом (четвертом) положении механизма выполняется по формулам:
Следует отметить, что в этих формулах длины отрезков измеряются в миллиметрах. Расчет скоростей выполняется для 12 положений механизма. Результаты расчета должны быть представлены в табличной форме (см. табл. 1.1). Таблица 1.1
Расчет ускорений
При кинематическом анализе механизма считается, что кривошип вращается с постоянной угловой скоростью, тогда ускорение
Ускорение
где Ускорение Величина нормальной составляющей относительного ускорения в соответствии с [1-3] вычисляется по формуле
Ускорение Уравнение (1.3) имеет два неизвестных, графическое его решение для 4-го положения механизма приведено на рис. 1.3.
Рис. 1.3. План ускорений
Для решения уравнения (1.3) выбирается масштабный коэффициент
Обозначим длину отрезка, изображающего на плане ускорений ускорение
Для решения уравнения (1.3) на поле чертежа (рис. 1.3) выбирается точка Ускорение
Из этой пропорции следует, что Отрезок Для определения ускорение
Откуда Отрезок Расчет ускорений:
Угловое ускорение шатуна вычисляется по формуле:
Расчет ускорений выполняется для 2-х положений механизма, результаты должны быть представлены в табличной форме (табл. 1.2).
Таблица 1.2
Силовой расчет механизма В ходе силового расчета определяются реакции в кинематических парах; уравновешивающие силы ( Расчет выполняется двумя методами – методом планов и методом рычага Жуковского.
2.1. Силовой расчет механизма методом планов Метод планов базируется на принципах Даламбера и заменяемости связей. Порядок силового расчета определяется формулой строения механизма [1-3]. Расчет проводят, начиная с наиболее удаленной от исходного механизма структурной группы, и заканчивают расчетом исходного механизма. Поскольку в рассматриваемом примере только одна структурная группа, расчет начинается с нее. Исходными данными для расчета являются: кинематическая схема; все кинематические размеры; массы звеньев m1, m2, m3; положения центров масс S1 и S2 кривошипа и шатуна; данные кинематического расчета; диаграмма силы полезного сопротивления и ее максимальное значение Р (рис. 2.1).
Рис. 2.1 Силовой расчет структурной группы Кинетостатический расчет механизма выполняется для двух его положений (например, 4 и 5). Расчет начинается с определения внешних сил, действующих на звенья, входящие в структурную группу. К ним относятся силы тяжести G2 и G3, силы инерции, сила полезного сопротивления Рпс. Сила тяжести i-го звена (i = 2, 3) вычисляется по формуле [1-3]
где mi - масса i-го звена; g – ускорение свободного падения, g = 9,8 м/с2. Сила тяжести шатуна
Сила тяжести ползуна
В соответствии с принципом Даламбера вычисляем силы инерции ползуна и шатуна. Для расчета сил инерции звеньнв механизма используется инженерный метод, метод замещающих точечных масс [1]. Согласно этому методу шатун заменим двумя точечными массами mА2 и mВ2, расположенными в центрах шарниров А и В соответственно. Точечные массы вычисляются по формулам:
Силы инерции замещающих масс вычисляются по следующим расчетным зависимостям[1-3]:
Сила инерции ползуна
Для определения силы полезного сопротивления РПСj в рассматриваемом 4–м положении механизма над разметкой (или под ней) строится диаграмма силы полезного сопротивления (рис. 2.2). Ось абсцисс диаграммы параллельна направляющей t-t ползуна, а начало ее системы координат совпадает с точкой В0 на разметке. Ось ординат направлена перпендикулярно t-t. Масштабный коэффициент μР диаграммы РПС(SВ) вычисляется по формуле
где Для определения значения РПС4 силы полезного сопротивления в рассматриваемом 4-м положении механизма из точки В4 на траектории движения ползуна (рис. 2.2) восстанавливаем перпендикуляр к оси t-t до пересечения с графиком РПС(SВ). Измеряем ординату
Рис. 2.2
Для расчета сил, действующих в кинематических парах структурной группы, составляем схему ее нагружения. Изображаем в масштабе
Рис. 2.3. Схема нагружения структурной группы
Силы тяжести G2 и G3 направлены вертикально вниз, точками их приложения являются центр масс Под действием указанной системы сил структурная группа находится в равновесии. В равновесии находится и каждое звено этой группы. Реакция
Плечи сил измеряются в мм на схеме нагружения.
Знак реакции Условие равновесия системы сил, действующих на структурную группу:
Уравнение (2.1) решается графически. Для этого выбираем масштабный коэффициент
где Вычисляем длины отрезков, которыми известные силы будут изображаться на плане сил (рис. 2.4), по формулам:
На свободном поле чертежа (рис.2.4) выбираем точку
Рис. 2.4. План сил
параллельную t-t,и в направлении действия силы инерции
Точку приложения реакции
Реакция Для определения реакции в шарнире В надо рассмотреть равновесие системы сил, действующих на шатун или ползун. Рассмотрим равновесие системы сил, действующих на ползун. Оно описывается уравнением
В уравнении (2.2) неизвестна сила
Силовой расчет кривошипа Предположим, что привод механизма осуществляется через муфту. Тогда на кривошип действуют силы тяжести Сила тяжести кривошипа:
Для расчеты сил инерции кривошипа заменяем его двумя точечными массами массами mА1 и mО1, расположенными в центрах шарниров А и О соответственно.
Точка О неподвижна, поэтому сила инерции массы mО1 равна нулю. Сила инерции массы mА1 [1-3]:
Сила Реакция
Реакция
Рис. 2.5
Под действием указанной на схеме нагружения системы сил кривошип находится в равновесии, следовательно
Реакция
План сил, действующих на кривошип, приведен на рис. 2.5, б. При его построении использовался масштабный коэффициент Для решения векторного уравнения (2.3) надо вычислить длины отрезков, изображающих известные силы.
На свободном поле чертежа (рис. 2.5, б) выбираем точку
Результаты силового расчета должны быть представлены в табличной форме (табл. 2.1) Таблица 2.1
|




 . Он показывает сколько метров длины содержится в одном миллиметре чертежа и вычисляется по формуле
. Он показывает сколько метров длины содержится в одном миллиметре чертежа и вычисляется по формуле , (1.1)
, (1.1) - длина кривошипа, м; ОА - длина отрезка, которым кривошип изображается на чертеже, мм.
- длина кривошипа, м; ОА - длина отрезка, которым кривошип изображается на чертеже, мм. , которыми на разметке будут изображаться шатун и дезаксиал е, вычисляются по формулам:
, которыми на разметке будут изображаться шатун и дезаксиал е, вычисляются по формулам: ,
,  .
. , изображающую направляющую ползуна.
, изображающую направляющую ползуна. , а кривошип и шатун вытягиваются в одну прямую или складываются. Чтобы получить крайние положения механизма, надо на траектории движения ползуна из точки О сделать засечки раствором циркуля
, а кривошип и шатун вытягиваются в одну прямую или складываются. Чтобы получить крайние положения механизма, надо на траектории движения ползуна из точки О сделать засечки раствором циркуля  и
и  . Получим точки В* и В**, соответствующие крайним положениям ползуна. Отрезок В*В** в масштабе
. Получим точки В* и В**, соответствующие крайним положениям ползуна. Отрезок В*В** в масштабе 
 кривошипа и
кривошипа и  шатуна и строятся траектории их движения. Для этого вычисляются длины отрезков
шатуна и строятся траектории их движения. Для этого вычисляются длины отрезков  и
и  .
. ,
,  .
. угловой скорости кривошипа определяется скорость его точки А [1-3]:
угловой скорости кривошипа определяется скорость его точки А [1-3]: = . . . = . . . м/с.
= . . . = . . . м/с.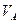 направлен перпендикулярно кривошипу в рассматриваемом его положении в сторону вращения.
направлен перпендикулярно кривошипу в рассматриваемом его положении в сторону вращения.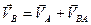 , (1.2)
, (1.2) - переносная скорость точки В;
- переносная скорость точки В;  - относительная скорость точки В;
- относительная скорость точки В;  - абсолютная скорость точки В.
- абсолютная скорость точки В. .
. ,
, - длина отрезка, которым скорость
- длина отрезка, которым скорость  (полюс плана скоростей). Из этой точки проводим луч, перпендикулярный ОА4, и откладываем на нем отрезок
(полюс плана скоростей). Из этой точки проводим луч, перпендикулярный ОА4, и откладываем на нем отрезок 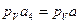 . Он изображает в масштабе
. Он изображает в масштабе  плана скоростей проводим луч, перпендикулярный шатуну в 4-м положении механизма (перпендикулярный
плана скоростей проводим луч, перпендикулярный шатуну в 4-м положении механизма (перпендикулярный  ), а из полюса
), а из полюса  . Отрезок
. Отрезок  плана скоростей изображает в масштабе
плана скоростей изображает в масштабе  , а отрезок
, а отрезок  - абсолютную скорость
- абсолютную скорость  точки В в 4-м положении механизма.
точки В в 4-м положении механизма. и
и  центров масс звеньев определяются по свойству подобия плана скоростей. Составляем пропорцию:
центров масс звеньев определяются по свойству подобия плана скоростей. Составляем пропорцию: .
.
 .
.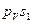 откладываем на плане скоростей (рис. 1.2) от полюса на прямой
откладываем на плане скоростей (рис. 1.2) от полюса на прямой  , получаем точку s1. Отрезок
, получаем точку s1. Отрезок  центра масс кривошипа.
центра масс кривошипа. центра масс шатуна составляем пропорцию:
центра масс шатуна составляем пропорцию: и вычисляем длину отрезка
и вычисляем длину отрезка  плана скоростей.
плана скоростей. .
. . Соединяем ее с полюсом плана скоростей. Отрезок
. Соединяем ее с полюсом плана скоростей. Отрезок  изображает скорость точки
изображает скорость точки  = = м/с;
= = м/с; = = м/с;
= = м/с; = = м/с;
= = м/с; = = м/с;
= = м/с; = = 1/с.
= = 1/с. точки А вычисляется по формуле [1-3]:
точки А вычисляется по формуле [1-3]: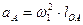 = = м/с2.
= = м/с2. точки В шатуна связано с ускорением его точки А зависимостью [1-3]:
точки В шатуна связано с ускорением его точки А зависимостью [1-3]: , (1.3)
, (1.3) и
и  - нормальная и тангенциальная составляющие относительного ускорения точки В.
- нормальная и тангенциальная составляющие относительного ускорения точки В.
 = = м/с2.
= = м/с2.
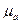 плана ускорений:
плана ускорений: = = м/(с2·мм).
= = м/(с2·мм). . Его длина вычисляется по формуле
. Его длина вычисляется по формуле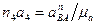 = = мм.
= = мм. , из нее проводится луч, параллельно ОА4. На этом луче от точки
, из нее проводится луч, параллельно ОА4. На этом луче от точки  . Из точки
. Из точки  плана ускорений проводим луч, параллельный шатуну в 4-м (параллельно
плана ускорений проводим луч, параллельный шатуну в 4-м (параллельно  проводим перпендикуляр (это линия действия тангенциальной составляющей относительного ускорения). Из полюса
проводим перпендикуляр (это линия действия тангенциальной составляющей относительного ускорения). Из полюса  плана ускорений изображает в масштабе
плана ускорений изображает в масштабе 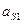 и
и  центров масс звеньев определяются по свойству подобия плана ускорений. Для расчета
центров масс звеньев определяются по свойству подобия плана ускорений. Для расчета  .
. .
. откладываем на плане ускорений (рис. 1.3) от полюса на прямой
откладываем на плане ускорений (рис. 1.3) от полюса на прямой  , получаем точку s1. Отрезок
, получаем точку s1. Отрезок  центра масс кривошипа.
центра масс кривошипа. .
. изображает ускорение точки
изображает ускорение точки  = = м/с2;
= = м/с2; = = м/с2;
= = м/с2; = = м/с2;
= = м/с2; = = м/с2;
= = м/с2; = = м/с2.
= = м/с2. = = 1/с2.
= = 1/с2.




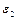
 ) или уравновешивающий момент (
) или уравновешивающий момент (  ).
).
 ,
, = = Н.
= = Н. = = Н.
= = Н. ;
;  .
. = = Н;
= = Н; = = Н.
= = Н. .
. ,
, - длина отрезка, которым максимальное значение силы Р изображается на диаграмме. Длина отрезка выбирается
- длина отрезка, которым максимальное значение силы Р изображается на диаграмме. Длина отрезка выбирается 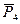 в миллиметрах. Величина силы полезного сопротивления вычисляется по формуле
в миллиметрах. Величина силы полезного сопротивления вычисляется по формуле = = Н.
= = Н.
 ;
;  и
и  ), силу полезного сопротивления РПС и реакции связей
), силу полезного сопротивления РПС и реакции связей  ,
,  ,
,  .
.
 направлена по шатуну АВ, тангенциальная составляющая
направлена по шатуну АВ, тангенциальная составляющая  .
. = = Н.
= = Н. . (2.1)
. (2.1) плана сил:
плана сил: ,
, - длина отрезка, которым сила полезного сопротивления изображается на плане сил.
- длина отрезка, которым сила полезного сопротивления изображается на плане сил. ;
;  ;
;  ;
;  ;
; ;
;  ;
;  .
. , из нее проводим луч параллельно линии действия силы
, из нее проводим луч параллельно линии действия силы  . Из точки
. Из точки  проводим луч параллельно линии действия силы
проводим луч параллельно линии действия силы  , изображающий эту силу. Из точки
, изображающий эту силу. Из точки  проводим прямую,
проводим прямую,
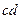 , изображающий в масштабе
, изображающий в масштабе  проводим линию действия силы силы тяжести шатуна и откладываем на ней в мм отрезок
проводим линию действия силы силы тяжести шатуна и откладываем на ней в мм отрезок  , изображающий G2. Из точки
, изображающий G2. Из точки  проводим прямую, параллельную t-t,и откладываем на ней отрезок
проводим прямую, параллельную t-t,и откладываем на ней отрезок  , изображающий в масштабе
, изображающий в масштабе  проводим линию действия силы G3 и откладываем на ней вниз в мм отрезок
проводим линию действия силы G3 и откладываем на ней вниз в мм отрезок  . Из точки
. Из точки  проводим прямую, параллельную t-t,и откладываем на ней в направлении действия силы РПС4 отрезок
проводим прямую, параллельную t-t,и откладываем на ней в направлении действия силы РПС4 отрезок  , изображающий в масштабе
, изображающий в масштабе  ) проводим перпендикуляр кпрямой
) проводим перпендикуляр кпрямой  ). Отрезок
). Отрезок  изображает в масштабе
изображает в масштабе  - реакцию
- реакцию  ;
;  ;
;  .
. определяем по условию равновесия системы сил, действующих на ползун.
определяем по условию равновесия системы сил, действующих на ползун. .
. . Таким образом, линия действия реакции
. Таким образом, линия действия реакции  . (2.2)
. (2.2)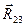 по величине и ипо направлению. Для ее пределения решим векторное уравнение (2.2). Для этого на плане сил (рис. 2.4) соединим точки
по величине и ипо направлению. Для ее пределения решим векторное уравнение (2.2). Для этого на плане сил (рис. 2.4) соединим точки  в масштабе
в масштабе 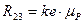 .
. , инерции
, инерции  , рекции
, рекции  ,
,  и уравновешивающий момент
и уравновешивающий момент  .
. ;
;  .
. .
. .
.
 .
.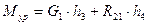 .
. . (2.3)
. (2.3) . . . Н/мм. Следует отметить, что при решении векторных уравнений (2.2) и (2.3) масштабные коэффициенты планов сил могут быть как одинаковыми, так и разными.
. . . Н/мм. Следует отметить, что при решении векторных уравнений (2.2) и (2.3) масштабные коэффициенты планов сил могут быть как одинаковыми, так и разными. ;
;  ;
;  .
. . Поскольку кривошип находится в равновесии, соединим точки
. Поскольку кривошип находится в равновесии, соединим точки  на плане сил изображает в принятом масштабе искомую реакцию
на плане сил изображает в принятом масштабе искомую реакцию  .
.