 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Линейные неоднородные дифференциальные уравнения со специальной правой частью
В двух частных случаях, когда правая часть уравнения (14) имеет вид  , где , где  – многочлен – многочлен  -й степени, -й степени,  – число, или – число, или  , где , где  – многочлены степени – многочлены степени  и и  , соответственно, , соответственно,  – числа, частное решение – числа, частное решение  уравнения (14) можно найти методом неопределенных коэффициентов. уравнения (14) можно найти методом неопределенных коэффициентов. А именно, пусть правая часть имеет вид  . Если . Если  не совпадает ни с одним корнем характеристического уравнения, то частное решение не совпадает ни с одним корнем характеристического уравнения, то частное решение  ищется в виде ищется в виде  , (26) , (26)
где  – многочлен той же степени, что и – многочлен той же степени, что и  , но с неопределенными коэффициентами, которые надо найти. Для чего, вычисляя с помощью (26) , но с неопределенными коэффициентами, которые надо найти. Для чего, вычисляя с помощью (26)  и подставляя в исходное уравнение (14), сокращаем правую и левую части на и подставляя в исходное уравнение (14), сокращаем правую и левую части на 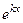 . Приравнивая коэффициенты при одинаковых степенях . Приравнивая коэффициенты при одинаковых степенях  , получим систему уравнений для отыскания неопределенных коэффициентов. Подставив их в (26), будем иметь искомое частное решение , получим систему уравнений для отыскания неопределенных коэффициентов. Подставив их в (26), будем иметь искомое частное решение  . . Если  совпадает с некоторым корнем характеристического уравнения кратности совпадает с некоторым корнем характеристического уравнения кратности  , то частное решение ищется в виде , то частное решение ищется в виде  . (27) . (27)
Дальнейшие действия аналогичны предыдущему случаю. Пусть теперь правая часть уравнения (14) имеет вид  . . Если число  не совпадает ни с одним из корней характеристического уравнения, то частное решение ищется в виде не совпадает ни с одним из корней характеристического уравнения, то частное решение ищется в виде  , (28) , (28)
где  , ,  и и  многочлены одной и той же степени многочлены одной и той же степени  , но с разными неопределенными коэффициентами, которые находятся так же, как и в первом случае. , но с разными неопределенными коэффициентами, которые находятся так же, как и в первом случае. Если  совпадает с некоторым корнем характеристического уравнения кратности совпадает с некоторым корнем характеристического уравнения кратности  , то выражение для частного решения (28) умножается на , то выражение для частного решения (28) умножается на  , а именно , а именно  , (29) , (29)
где  , ,  , ,  те же, что и выше. те же, что и выше. Замечание 1. Если в правой части  один из многочленов один из многочленов  или или  нулевой (т.е. нулевой (т.е.  или или  ), то вид частного решения не меняется, т.е. ), то вид частного решения не меняется, т.е.  ищется в форме (28) или (29). ищется в форме (28) или (29). Замечание 2. Многочлены с неопределенными коэффициентами четвертой, третьей, второй, первой, нулевой степени имеют вид: 
где  неопределенные коэффициенты; многочлены неопределенные коэффициенты; многочлены  и и   выписываются аналогично выписываются аналогично  . . Примеры. 1. Для каждого из данных неоднородных дифференциальных уравнений написать вид его общего и частного решений с неопределенными коэффициентами (числовые значения коэффициентов не находить): а)  , б) , б)  . . 2. Найти общие решения следующих уравнений: в)  , г) , г)  . . Решение.а) Рассмотрим уравнение  . Ищем общее решение в виде . Ищем общее решение в виде  . Характеристическое уравнение . Характеристическое уравнение 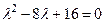 имеет корни имеет корни  , т.е. кратность , т.е. кратность  корня корня  равна 2. Согласно формуле (25) общее решение соответствующего однородного уравнения равна 2. Согласно формуле (25) общее решение соответствующего однородного уравнения  . . Для того, чтобы выписать частное решение 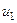 проанализируем правую часть проанализируем правую часть  , где , где  – многочлен 1-й степени, т.е. – многочлен 1-й степени, т.е.  , тогда , тогда   , т.е. , т.е.  совпадает с одним корнем кратности 2 характеристического уравнения, следовательно, имеет место формула (27): совпадает с одним корнем кратности 2 характеристического уравнения, следовательно, имеет место формула (27):  , где , где  и и  неопределенные коэффициенты. Общее решение исходного уравнения имеет вид неопределенные коэффициенты. Общее решение исходного уравнения имеет вид  . .
б) Для уравнения  соответствующее характеристическое уравнение соответствующее характеристическое уравнение  имеет кратные корни имеет кратные корни  , ,  , т.е. , т.е.  . Согласно формуле (24) с учетом кратности корней получим общее решение соответствующего однородного уравнения . Согласно формуле (24) с учетом кратности корней получим общее решение соответствующего однородного уравнения 
Для того, чтобы выписать частное решение  анализируем правую часть анализируем правую часть  , где , где  т.е. т.е.   . Следовательно, многочлены с неопределенными коэффициентами . Следовательно, многочлены с неопределенными коэффициентами  и и  имеют одну и ту же степень имеют одну и ту же степень  , но разные коэффициенты, т.е. , но разные коэффициенты, т.е. 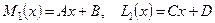 . Составим число . Составим число  (так как (так как  ), поскольку ), поскольку  не совпадает ни с одним корнем характеристического уравнения, то частное решение не совпадает ни с одним корнем характеристического уравнения, то частное решение  ищем в виде (28) ищем в виде (28)  , а общее решение , а общее решение  есть есть   . .
в) Общее решение уравнения  ищется в виде ищется в виде  . Характеристическое уравнение . Характеристическое уравнение  имеет корни имеет корни  . Общее решение соответствующего однородного уравнения есть . Общее решение соответствующего однородного уравнения есть  . . Правая часть неоднородного уравнения  , где , где  , откуда , откуда  совпадает с одним корнем характеристического уравнения совпадает с одним корнем характеристического уравнения  , следовательно, по формуле (27) частное решение имеет вид: , следовательно, по формуле (27) частное решение имеет вид:  , где , где  неопределенный коэффициент. Найдем его методом неопределенных коэффициентов, для чего, подставив неопределенный коэффициент. Найдем его методом неопределенных коэффициентов, для чего, подставив   , ,  в исходное уравнение, будем иметь в исходное уравнение, будем иметь  . Сократим последнее уравнение на . Сократим последнее уравнение на  , получим , получим  . Приравняем коэффициенты при одинаковых степенях . Приравняем коэффициенты при одинаковых степенях  . .
Так как неопределенный коэффициент найден,  , то частное решение имеет вид: , то частное решение имеет вид:  , следовательно, общее решение исходного уравнения запишется в форме: , следовательно, общее решение исходного уравнения запишется в форме:  . .
г) Уравнение  это уравнение с правой частью это уравнение с правой частью  второго типа, его общее решение ищется в виде второго типа, его общее решение ищется в виде  . . Характеристическое уравнение  имеет корни имеет корни 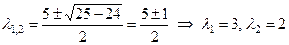 . .
Общее решение  однородного уравнения выписывается по формуле (23): однородного уравнения выписывается по формуле (23): 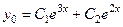 . .
Для отыскания частного решения  анализируем правую часть анализируем правую часть  , здесь , здесь  тогда тогда  число число  не совпадает с корнями характеристического уравнения, следовательно, не совпадает с корнями характеристического уравнения, следовательно,  выписываем по формуле (28): выписываем по формуле (28): 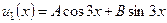 . . Неопределенные коэффициенты  и и  находятся так: находятся так: 1) Считаем  . . 2) Подставляем  в исходное уравнение: в исходное уравнение: 
или  . .
3) Приравнивая коэффициенты при  и и  , стоящие в правой и левой частях последнего уравнения, получим систему для определения коэффициентов , стоящие в правой и левой частях последнего уравнения, получим систему для определения коэффициентов  и и  : :  . .
4) Итак, частное решение имеет вид 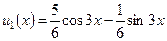 , следовательно, общее решение исходного уравнения запишется в форме: , следовательно, общее решение исходного уравнения запишется в форме:   . .
|




 , где
, где  – многочлен
– многочлен  -й степени,
-й степени,  – число, или
– число, или  , где
, где  – многочлены степени
– многочлены степени  , соответственно,
, соответственно,  – числа, частное решение
– числа, частное решение  уравнения (14) можно найти методом неопределенных коэффициентов.
уравнения (14) можно найти методом неопределенных коэффициентов. . Если
. Если  , (26)
, (26) – многочлен той же степени, что и
– многочлен той же степени, что и  и подставляя в исходное уравнение (14), сокращаем правую и левую части на
и подставляя в исходное уравнение (14), сокращаем правую и левую части на 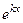 . Приравнивая коэффициенты при одинаковых степенях
. Приравнивая коэффициенты при одинаковых степенях  , получим систему уравнений для отыскания неопределенных коэффициентов. Подставив их в (26), будем иметь искомое частное решение
, получим систему уравнений для отыскания неопределенных коэффициентов. Подставив их в (26), будем иметь искомое частное решение  совпадает с некоторым корнем характеристического уравнения кратности
совпадает с некоторым корнем характеристического уравнения кратности  , то частное решение ищется в виде
, то частное решение ищется в виде . (27)
. (27) .
. не совпадает ни с одним из корней характеристического уравнения, то частное решение ищется в виде
не совпадает ни с одним из корней характеристического уравнения, то частное решение ищется в виде , (28)
, (28) ,
,  и
и  многочлены одной и той же степени
многочлены одной и той же степени  , но с разными неопределенными коэффициентами, которые находятся так же, как и в первом случае.
, но с разными неопределенными коэффициентами, которые находятся так же, как и в первом случае. , а именно
, а именно , (29)
, (29) те же, что и выше.
те же, что и выше. один из многочленов
один из многочленов  нулевой (т.е.
нулевой (т.е.  или
или  ), то вид частного решения не меняется, т.е.
), то вид частного решения не меняется, т.е. 
 неопределенные коэффициенты; многочлены
неопределенные коэффициенты; многочлены  выписываются аналогично
выписываются аналогично  , б)
, б)  .
. , г)
, г)  .
. . Характеристическое уравнение
. Характеристическое уравнение 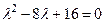 имеет корни
имеет корни  , т.е. кратность
, т.е. кратность  равна 2. Согласно формуле (25) общее решение соответствующего однородного уравнения
равна 2. Согласно формуле (25) общее решение соответствующего однородного уравнения  .
.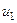 проанализируем правую часть
проанализируем правую часть  , где
, где  – многочлен 1-й степени, т.е.
– многочлен 1-й степени, т.е.  , тогда
, тогда 
 , т.е.
, т.е.  , где
, где  и
и  неопределенные коэффициенты. Общее решение исходного уравнения имеет вид
неопределенные коэффициенты. Общее решение исходного уравнения имеет вид .
. имеет кратные корни
имеет кратные корни  ,
,  , т.е.
, т.е.  . Согласно формуле (24) с учетом кратности корней получим общее решение соответствующего однородного уравнения
. Согласно формуле (24) с учетом кратности корней получим общее решение соответствующего однородного уравнения
 , где
, где  т.е.
т.е. 
 . Следовательно, многочлены с неопределенными коэффициентами
. Следовательно, многочлены с неопределенными коэффициентами  имеют одну и ту же степень
имеют одну и ту же степень  , но разные коэффициенты, т.е.
, но разные коэффициенты, т.е. 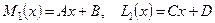 . Составим число
. Составим число  (так как
(так как  ), поскольку
), поскольку  , а общее решение
, а общее решение 
 .
. . Характеристическое уравнение
. Характеристическое уравнение  имеет корни
имеет корни  . Общее решение соответствующего однородного уравнения есть
. Общее решение соответствующего однородного уравнения есть  .
. , где
, где  , откуда
, откуда  совпадает с одним корнем характеристического уравнения
совпадает с одним корнем характеристического уравнения  , следовательно, по формуле (27) частное решение имеет вид:
, следовательно, по формуле (27) частное решение имеет вид:  , где
, где  неопределенный коэффициент. Найдем его методом неопределенных коэффициентов, для чего, подставив
неопределенный коэффициент. Найдем его методом неопределенных коэффициентов, для чего, подставив 
 ,
,  в исходное уравнение, будем иметь
в исходное уравнение, будем иметь  . Сократим последнее уравнение на
. Сократим последнее уравнение на  , получим
, получим  . Приравняем коэффициенты при одинаковых степенях
. Приравняем коэффициенты при одинаковых степенях .
. , то частное решение имеет вид:
, то частное решение имеет вид:  , следовательно, общее решение исходного уравнения запишется в форме:
, следовательно, общее решение исходного уравнения запишется в форме: .
. это уравнение с правой частью
это уравнение с правой частью  второго типа, его общее решение ищется в виде
второго типа, его общее решение ищется в виде  .
. имеет корни
имеет корни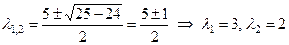 .
. однородного уравнения выписывается по формуле (23):
однородного уравнения выписывается по формуле (23):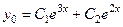 .
. , здесь
, здесь  тогда
тогда  число
число  не совпадает с корнями характеристического уравнения, следовательно,
не совпадает с корнями характеристического уравнения, следовательно, 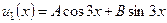 .
. и
и  находятся так:
находятся так: .
. в исходное уравнение:
в исходное уравнение:
 .
. и
и  , стоящие в правой и левой частях последнего уравнения, получим систему для определения коэффициентов
, стоящие в правой и левой частях последнего уравнения, получим систему для определения коэффициентов  .
.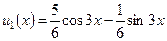 , следовательно, общее решение исходного уравнения запишется в форме:
, следовательно, общее решение исходного уравнения запишется в форме:
 .
.