 ПОЗНАВАТЕЛЬНОЕ
| РАЗРАБОТКА МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ХИМИКО-ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
УДК 541.1 Любименко В.А., Семёнов А.П., Виноградов В.М., Винокуров В.А. Разработка математического описания химико-технологических процессов: Метод. указ. для выполнения домашнего задания по курсу «Моделирование химико-технологических процессов» - М.: РИЦ РГУ нефти и газа им. И.М. Губкина, 2013. - 35 с. Методические указания включают краткую теоретическую часть и подробное рассмотрение методики разработки математического описания химико-технологических процессов на конкретном примере сложной химической реакции, протекающей в потоке. При этом показаны основные подходы при выборе метода решения разработанного математического описания с применением ЭВМ. Рассмотрено решение математического описания средствами пакета MATLAB. Настоящие методические указания предназначены для бакалавров, обучающихся по направлению 240100 – Химическая технология, по профилям 240401 – Химическая технология органических веществ и 240403 – Химическая технология природных энергоносителей и углеродных материалов, а также для специалистов при выполнении ими домашнего задания по курсу "Моделирование в химической технологии", что способствует закреплению знаний теоретического и практического материала. Навыки и знания, полученные в процессе выполнения домашнего задания необходимы как будущим технологам, так и научным сотрудникам. Работа рекомендована к изданию решением учебно-методической комиссии факультета химической технологии и экологии. Рецензент – профессор, д.х.н. И. М. Колесников
ВВЕДЕНИЕ На завершающем этапе изучения курса "Моделирование в химической технологии" бакалавры, обучающихся по направлению 240100 Химическая технология, и специалисты выполняют домашнее задание, целью которого является закрепление полученных теоретических знаний на примере индивидуального задания по разработке математического описания химико-технологического процесса (ХТП) и его решения с помощью ЭВМ.
НЕКОТОРЫЕ ВОПРОСЫ ХИМИЧЕСКОЙ КИНЕТИКИ
На этапе анализа, описания и расчета химико-технологических процессов (ХТП) вопрос о механизме протекающих химических реакций чаще всего не встает, т.е. кинетические закономерности рассматриваются заданными. Если это не так, то сначала необходимо выполнить этап физико-химических исследований (экспериментальных или литературных), связанных с изучением кинетики данного химического процесса (найти порядок реакций по реагентам, константы скорости отдельных стадий, энергии активации и т.д.). В наиболее общем виде домашнее задание можно сформулировать следующим образом: разработать математическое описание и решить его с помощью ЭВМ для химического процесса, протекающего в потоке идеального вытеснения (ИВ) или потоке идеального смешения (ИС) в изотермических условиях и постоянном давлении по заданной схеме процесса. При этом схема процесса представляет собой сложную химическую реакцию, протекающую в 4-5 стадий. Для удобства изложения мы будем рассматривать методику выполнения задания на примере реакции:
Прежде чем начать работу над заданием, необходимо определиться относительно структуры математического описания. Как известно, математическое описание (математическая модель) физико-химического процесса представляет собой систему уравнений балансов масс компонентов, тепла и кинетической энергии, которые в дальнейшем используются для построения полей (профилей) концентраций, температуры и давления в аппарате. В нашем случае, поскольку процесс протекает при постоянной температуре и постоянном давлении, уравнения теплового баланса и баланса кинетической энергии составлять не нужно. Следовательно, математическое описание изучаемого процесса будет состоять из уравнений материального баланса, а число этих уравнений будет равно числу участников заданной реакции. Прежде всего, следует напомнить некоторые важнейшие понятия химической кинетики, которые необходимы для технически грамотного подхода к разработке математического описания. Практика показывает, что подавляющее большинство ошибок допускается студентами на начальном этапе работы и, как правило, от незнания (или забывчивости) азов химической кинетики. Это тем более важно потому, что вся последующая работа не дает возможности обнаружить и исключить допущенные ошибки: они обычно обнаруживаются только после выполнения счета на ЭВМ. В химической кинетике все реакции разделяют на два вида: простые и сложные. Простая химическая реакция содержит один элементарный акт, то есть протекает в одну стадию. Однако на практике такие истинно одностадийные реакции встречаются крайне редко. В формальной кинетике часто говорят о формально простых реакциях. Так называют реакции, которые формально можно представить как протекающие в одну стадию. В действительности реакция может быть сложной, проходящей через какие-то промежуточные стадии, но если в условиях рассматриваемой задачи промежуточные продукты не обнаруживаются, то реакция может рассматриваться как формально простая. Несмотря на условность этого понятия, оно удобно и поэтому часто используется. Подавляющее большинство химических реакций всегда приходится рассматривать как сложные: они явно распадаются на отдельные стадии (продукты различных стадий образуются в значительных количествах). Выделяют три простейших типа сложных реакций: - обратимые реакции - сложные реакции, состоящие из двух стадий: прямой и обратной реакции, А - параллельные реакции - сложные реакции, в которых исходное вещество по двум или нескольким параллельным направлениям (реакциям, стадиям) превращается в два или несколько продуктов, А А - последовательные реакции - сложные реакции, когда продукт первой стадии является исходным веществом для второй стадии и так далее, А Все остальные сложные реакции можно представить в виде комбинаций трех приведенных выше типов реакций. Скорость реакции - основное понятие химической кинетики. Она определяется как количество вещества, реагирующее в единицу времени в единице реакционного пространства, W = dn/Vdt, (1) где V - реакционное пространство, которое в случае гомогенной реакции представляет собой объем, а в случае гетерогенной - поверхность, n - число молей реагирующего вещества, t - время. Вводя мольно-объемную концентрацию c реагирующего вещества, в общем случае получаем:
или
Если гомогенная реакция протекает в закрытом объеме (не обменивается веществом с окружающей средой) в изохорических условиях (V = const), то второе слагаемое равно нулю и тогда: W = dc/dt. (2) Уравнением (2) часто пользуются, т.к. оно удобно для интегрирования, но необходимо помнить, что это лишь частный случай, который верен далеко не всегда. В случае простой (одностадийной) реакции
вопрос о скорости ее протекания решается довольно просто. Из по- нятия стехиометрической эквивалентности следует, что если за какое-то время прореагирует некоторое количество
Другими словами, не имеет значения, какие из этих величин Для единообразия скорость простой реакции (скорость стадии) принято определять, деля скорость, выраженную через любое i-oе вещество, участвующее в этой стадии, на стехиометрический коэффициент этого вещества W = Wi / ni. (5) В этом случае безразлично, какое из веществ принято в качестве i-го, так как из выражений (4) и (5) следует:
В практических формально-кинетических расчетах значения скоростей простых реакций или отдельных стадий (в случае сложных реакций), выраженные через конкретные вещества, используются довольно часто, т.е. выражение (5) чаще всего используется в виде: Wi = niW. (6) При этом следует иметь в виду, что скорость реакции (стадии), выраженная через конкретное i-e вещество, всегда имеет знак, показывающий, как ведет себя i-eвещество в рассматриваемой реакции: если i-e вещество расходуется, то Wi <0; если i-eвещество образуется, то Wi>0. Это получается из выражения (6) в соответствии с соглашением, что стехиометрические коэффициенты исходных веществ отрицательны (ni<0), а стехиометрические коэффициенты продуктов реакции положительны ( Скорость простых реакций (отдельных стадий сложных реакций) пропорциональна концентрациям реагирующих веществ в некоторых степенях. Показатели степени в таком случае называют порядком реакции по реагентам. Так, для реакции (3) функциональная зависимость скорости реакции от концентрации реагирующих веществ, называемая основным постулатом химической кинетики, выражается кинетическим уравнением:
где
На практике встречаются реакции самых разнообразных порядков: целочисленных и дробных, нулевого, а иногда и отрицательного. Порядок реакции по реагентам может совпадать со стехиометрическими коэффициентами, но такое совпадение обязательно только для действительно простых реакций. Следует отметить, что непосредственно вблизи равновесия порядок пореагентам сходится к стехиометрическим коэффициентам для всех реакций. Вместе с тем существуют реакции, скорость которых вообще не может быть описана формулой (7), например разветвленные цепные реакции. Для всех типов сложных реакций (кроме простейшей обратимой) понятие общей скорости реакции не имеет смысла, т.е. реакция протекает через ряд стадий, каждая из которых имеет свою скорость и невозможно сколько-нибудь естественным образом определить, что такое скорость всей сложной реакции в целом. В то же время любое из участвующих веществ образуется или расходуется с определенной скоростью. Скорость сложной реакции по любому i-му веществу равна алгебраической сумме скоростей всех стадий по этому веществу (с учётом стехиометрических коэффициентов):
где j - номер стадии (j = 1, 2, ..., т), т - число стадий в сложной реакции. Скорость стадии определяется по формуле (6). Если вещество не участвует в j-йстадии, его стехиометрический коэффициент равен нулю.
ИДЕАЛЬНЫЕ ПОТОКИ Большинство реальных ХТП проводится в потоке. Поток оказывает существенное влияние на ход процессов. В случае гомогенных реакций в основном достаточно знания кинетики процесса в потоке. Если же процесс гетерогенный, то сначала, как правило, необходимо учесть явления переноса, происходящие на границе раздела фаз. Любой поток сложен по своей структуре. Сложность проявляется на различных уровнях, в разных масштабах, ее проявления всегда многообразны. В разных частях потока скорости различны как по величине, так и по направлению. Крайние случаи неоднородности скоростей - это короткие байпасы и застойные зоны. Неоднородность скоростей по направлению может приводить к образованию зон циркуляции. Все это в конечном счете приводит к возникновению перемешивания в потоке и неравномерности времени пребывания. Поперечное перемешивание интенсифицирует массообмен между осевой частью потока и его периферией и тем самым, как правило, улучшает условия протекания реакции. Продольное перемешива-ние - это смешение частиц, которые только что вошли в аппарат с частицами, давно в нем находящимися, в которых процесс превращения уже зашёл далеко. Продольное перемешивание чаще всего снижает движущую силу процесса и ухудшает его показатели. Неоднородность времени пребывания - явление, в значительной мере эквивалентное продольному перемешиванию: для частиц, уходящих вперед, время пребывания меньше среднего; отстающие частицы характеризуются большим временем пребывания. Среднее время пребывания определяется простым соотношением: t = Va /U (9) где Va - объем аппарата, U - объемный расход. Для описания реальных потоков часто пользуются упрощенными мысленными моделями, называемыми идеальными моделями (потоками). Разработаны две модели идеальных потоков: идеального вытеснения (ИВ) и идеального смешения (ИС). Обе модели не содержат никаких параметров, отражающих специфику структуры потока, и единственным параметром этих моделей является среднее время пребывания (время контакта), определяемое по формуле (9). Существует довольно много задач, в которых описание реального потока моделью того или иного идеального потока оказывается достаточно точным. Если же точность такого приближения недостаточна, то переходят к более сложным моделям неидеальных потоков, учитывающих его характер. В аппарате ИВ поток движется совершенно равномерно, в любом сечении все частицы имеют одинаковую скорость, фронт потока движется как твердый поршень. Следовательно, время пребывания всех частиц в потоке ИВ одинаково. Выделив в потоке ИВ элементарный объем, занимающий все поперечное сечение, можно заключить, что ни одна частица не может ни войти в этот объем, ни выйти из него (для этого она должна двигаться с иной скоростью, чем все остальные) и, следовательно, этот объем можно рассматривать как замкнутый. Другими словами, уравнение материального баланса для любого i-го участника ХТП и стационарного потока ИВ V(dc/dl) = W, (10) где l - длина потока, V - линейная скорость потока, можно переписать в виде: dc/dt = W. (11) В аппарате ИС все, что входит в него, мгновенно и равномерно распределяется по всему объему: концентрация и температура равномерно распределены по объему аппарата, на выходе из аппарата концентрация и температура - те же, что в объеме. Однако время пребывания распределено неравномерно, и замкнутых объемов в аппарате нет. Вместе с тем то обстоятельство, что во всех точках аппарата концентрация и температура, а следовательно, и скорость реакции, одинаковы, позволяет довольно просто получить уравнение материального баланса. Для любого i-го реагента и стационарного режима ИС это уравнение имеет вид: V(Δc/l) = W (12) или, вводя среднее время пребывания в соответствии с (9), получим: Δс/t = W. (13) Для практических расчетов полученное уравнение записывают в более удобном виде: с 0 - c + t·W = 0, (14) где с0- концентрация i-гo вещества на входе, с - концентрация i-гoвещества на выходе. На основе изложенных теоретических основ химической кинетики сложных реакций, протекающих в идеальных потоках ИВ и ИС, рассмотрим методику выполнения домашнего задания.
РАЗРАБОТКА МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ХИМИКО-ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА В этом разделе подробно рассмотрим последовательность составления математического описания сложного ХТП, протекающего в потоке ИВ или ИС. При этом, как указано выше, для рассматриваемой реакции должны быть заданы кинетические параметры (порядки по реагентам, константы скоростей и т.д.). С учетом этого схему химического процесса запишем в виде:
Символика, принятая при такой записи реакции, имеет следующий смысл: ki - константы скоростей соответствующих стадий, 1B; 1C; 1D - первый порядок по веществам B, C и D; 1,5A - дробный (1,5) порядок по веществу A и т.д. И наконец, для выполнения численного расчета должны быть заданы начальные (на входе в аппарат) концентрации участников реакции, численные значения констант скоростей и пределы изменения аргумента t (времени пребывания). Пусть константы скорости для рассматриваемой реакции равны: k1=4; k2=2; k3=3; k4=3; k5=l,2 мин-1 (л/моль.мин); а начальные концентрации участников реакции: Методика решения. При составлении математического описания сложного ХТП рекомендуется следующий порядок работы. I. Перепишем заданную схему процесса таким образом, чтобы в каждой строке была одна простая (необратимая) стадия: слева - исходные вещества, справа - продукты реакции 1. 2. 3. 4. 5.
Каждая стадия имеет свою, вполне определенную скорость реакции, определяемую в соответствии с основным постулатом химической кинетики.
II. Теперь запишем уравнения скоростей каждой из пяти перечисленных выше стадий процесса (в соответствии с основным постулатом химической кинетики и заданными величинами порядков по реагентам):
Индексы у Wi соответствуют номеру простой реакции (стадии) в схеме (15).
III. В соответствии с (8) и заданной кинетической схемой процесса (15) запишем выражения для скоростей образования каждого из участников процесса. Для вещества А.Из кинетической схемы видно, что это вещество расходуется в стадии 1 (следовательно, знак "минус") со стехиометрическим коэффициентом 1 (следовательно, -W1,), образуется в стадии 2 (следовательно, знак "плюс") со стехиометрическим коэффициентом 1 (следовательно, +W2)и расходуется (знак "минус") в стадии 3 со стехиометрическим коэффициентом 1 (следовательно, -W3).Таким образом, окончательно получаем: WA = -Wl+ W2-W3. (17) Рассуждать можно и иначе (см. текст соглашения после формулы 6): вещество А участвует в 1-й, 2-й и 3-й стадиях со стехиометрическими коэффициентами -1, +1 и -1, соответственно. С учетом этих обстоятельств, для WА получим выражение (17). Для вещества В.Используя кинетическую схему (15), заключаем, что это вещество расходуется (знак "минус") в первой стадии со стехиометрическим коэффициентом 2 (следовательно, -2W1)и образуется (знак "плюс") во второй стадии со стехиометрическим коэффициентом 2 (следовательно, +2W2). Формальные рассуждения приводят к тому же результату: вещество В участвует в 1-й и 2-й стадиях со стехиометрическими коэффициентами -2 и +2, соответственно. Таким образом, получаем: WB= –2W1+2W2. (18) Рассматривая кинетическую схему (15) относительно образования и расходования остальных участников химического процесса, получим: WС= 3W1–3W2 – W4 + W5, (19) WD= W3– W4 + W5, (20) WE =2W4 – 2W5. (21) IV. Bo все выражения для скоростей образования участников химического процесса (17 - 21) подставим выражения для скоростей отдельных стадий (16):
Математическое описание рассматриваемого ХТП в потоке ИВ получается простой подстановкой уравнений (22) в уравнение (11):
Мы получили систему обыкновенных дифференциальных уравнений. В общем случае при выборе метода решения обычно руководствуются правилом: - в случае формально простой (а также обратимой) реакции математическое описание всегда приводится к дифференциальному уравнению с разделяющимися переменными. При этом уравнение решается аналитически; - в случае формально сложной реакции, если все стадии имеют первый (и/или нулевой) порядок, то система дифференциальных уравнении линейна и решается аналитически. Во всех остальных случаях, как правило, аналитическое решение невозможно, и рекомендуется применять методы численного интегрирования с помощью ЭВМ. Математическое описание рассматриваемого ХТП в потоке ИС получается путем подстановки выражений для Wi из уравнений (22) в уравнение (14):
Получаем систему нелинейных алгебраических уравнений, для решения которой обычно используется численный метод Ньютона-Рафсона. Решение системы уравнений (24) выполняют с применением ЭВМ. В общем случае выбор метода решения определяется видом полученных уравнений. Если все стадии имеют первый (и/или нулевой) порядок, то полученные уравнения образуют систему линейных алгебраических уравнений, которую можно решить аналитически или численно с помощью ЭВМ, например по алгоритму Гаусса. В случае формально простой (а также обратимой) реакции систему уравнений всегда можно свести к одному уравнению с одной неизвестной (например, выразив концентрации всех участников через степень превращения). При этом, как правило, получается нелинейное алгебраическое уравнение, которое можно решить иногда аналитически, а чаще численно, например методом половинного деления (дихотомии) или методом "золотого" сечения.
ВЫХОД В РАСЧЕТЕ НА СЫРЬЕ Иногда в соответствии с заданием все вычисления требуется выполнить "в расчете на сырьё", т.е. в расчете на одно (если их несколько) из исходных веществ. Это означает, что начальные и текущие концентрации участников процесса должны быть выражены в безразмерных единицах, т.е. в долях от исходной концентрации одного из исходных веществ. Пусть, например, необходимо решить нашу задачу в расчете на вещество В. В этом случае во все уравнения математического описания вводят новые (относительные, являющиеся безразмерными) концентрации, которые можно обозначить Yi:
где Начальные концентрации исходных веществ также необходимо выразить в относительных единицах
Из соотношений (25) и (26) выражаем концентрации ci и
Для того, чтобы получить математическое описание ХТП в потоке ИВ в расчете на сырье B, в уравнения (23) нужно подставить соотношения (27) и (28). В результате получим:
После сокращения всех уравнениях в системе (29) на числовой коэффициент
|



 .
. В;
В;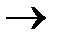 В
В С;
С; В
В  ,
, .
. (3)
(3) вещества А1, то за это же время количества реагирующего вещества А2 и образующихся продуктов
вещества А1, то за это же время количества реагирующего вещества А2 и образующихся продуктов  и
и  составят:
составят: ,
,  ,
, 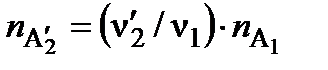 . (4)
. (4) ,
,  ,
,  или
или  . подставить в формулу (1). Правда, при этом мы получим численно разные величины
. подставить в формулу (1). Правда, при этом мы получим численно разные величины  ,
,  ,
,  или
или  . Однако, строго говоря, это одна и та же величина - скорость реакции (3), но выражена она в разных единицах.
. Однако, строго говоря, это одна и та же величина - скорость реакции (3), но выражена она в разных единицах.
 >0). Тогда, учитывая, что W всегда положительна (в соответствии с основным постулатом химической кинетики), получим для исходных веществ
>0). Тогда, учитывая, что W всегда положительна (в соответствии с основным постулатом химической кинетики), получим для исходных веществ  <0,
<0,  <0, а для продуктoв реакции
<0, а для продуктoв реакции  ,
,  .
. . (7)
. (7) ,
,  - порядок реакции по реагирующим веществам А1 и А2, соответственно,
- порядок реакции по реагирующим веществам А1 и А2, соответственно, +
+  , (8)
, (8) (15)
(15) =5;
=5;  =2;
=2; 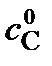 =
= 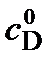 =
=  =0 моль/л. Расчеты необходимо выполнить с шагом не более 0,1 мин при условии, что предельное время контакта равно 2 мин.
=0 моль/л. Расчеты необходимо выполнить с шагом не более 0,1 мин при условии, что предельное время контакта равно 2 мин.






 , (16)
, (16)
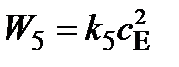 ,
, ,
, ,
, , (22)
, (22) ,
,
 ,
, ,
, , (23)
, (23) ,
, .
. ,
, ,
, , (24)
, (24) ,
,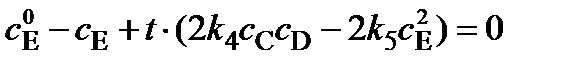 .
. ;
;  ;
;  ; ... , (25)
; ... , (25) ,
,  ,
,  - относительные текущие концентрации веществ A, B, C и т.д.
- относительные текущие концентрации веществ A, B, C и т.д. :
: ;
;  ;
;  ; ... . (26)
; ... . (26) :
: ;
;  ;
;  ; ... , (27)
; ... , (27)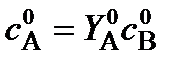 ;
;  ;
;  ; ... . (28)
; ... . (28) ,
, ,
, , (29)
, (29) ,
, .
. получаем:
получаем: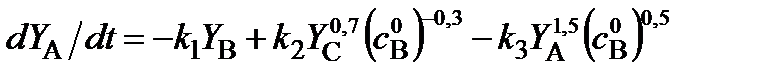 ,
, , (30)
, (30) ,
,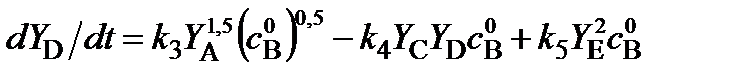 ,
, .
.
 Система уравнений (30) представляет собой математическое описание ХТП, протекающего в потоке ИВ, в расчете на сырье (вещество B). Начальная концентрация вещества B, как видно из уравнений системы (30), входит в них в виде числовой константы . Для правильного решения системы уравнений (30) в качестве начальных концентраций веществ подставляют их относительные значения в соответствии с (26).
Система уравнений (30) представляет собой математическое описание ХТП, протекающего в потоке ИВ, в расчете на сырье (вещество B). Начальная концентрация вещества B, как видно из уравнений системы (30), входит в них в виде числовой константы . Для правильного решения системы уравнений (30) в качестве начальных концентраций веществ подставляют их относительные значения в соответствии с (26).