 ПОЗНАВАТЕЛЬНОЕ
| Построение математической модели в относительных показателях
При выполнении определенных условий экономическая система, поведение которой описывается моделью Солоу, может иметь так называемую стационарную траекторию. При этом стационарной траекторией называют такое поведение экономической системы, когда ее показатели не изменяются во времени. Определим условия, выполнение которых приводит к неизменности относительных показателей экономической системы, описываемой моделью Солоу. Для этих целей введём относительные показатели: а) б) в) г) С учетом введенных относительных показателей можно записать: Пункт 1. Пункт 2.
или, используя третье уравнение из системы (11), получим:
Разделим данное уравнение на L(t) и разрешим его относительно
Пункт 3. Пункт 4. С учетом выведенных в пунктах 1-4 уравнений модель Солоу в относительных показателях можно записать в виде следующей системы уравнений:
Если установить неизменными во времени показатели:
Определение стационарной траектории Как видно из системы уравнений (12), выход на стационарную траекторию можно обеспечить путем установления фондовооруженности труда на постоянном уровне, т.е. при соблюдении условия, что В этом случае
Выражение (13) можно переписать в следующем виде:
Учитывая, что Х(t) = f [К(t), L(t)] является неоклассической функцией, то f(0)=0, f’>0, f”<0. Если дополнительно задать условие, что
то уравнение (14) будет иметь единственное ненулевое решение
h2(k) = f*(1-a)*f[k]
0 k` k0 k Рис. 1 Одинаковая скорость роста функций
Таким образом, решив уравнение (16), можно найти численное значение Если в начальный момент времени t=0 экономическая система имеет фондовооруженность, В случае если · если · если · если Аналогичным образом изменяются и остальные относительные показатели в модели Солоу, т.к. они связаны с фондовооруженностью труда. |



 - фондовооруженность труда;
- фондовооруженность труда; - производительность труда;
- производительность труда; - удельные инвестиции;
- удельные инвестиции;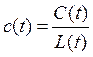 - среднедушевое потребление (на одного занятого).
- среднедушевое потребление (на одного занятого).


 В этом случае будем иметь:
В этом случае будем иметь: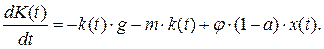


 (12)
(12)


 то экономическая система будет находиться на стационарной траектории.
то экономическая система будет находиться на стационарной траектории.
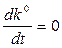 и, следовательно
и, следовательно (13)
(13) (14)
(14) (15)
(15) Данное положение показано на рис. 1
Данное положение показано на рис. 1




 h(k)
h(k) h1(k) = l*k
h1(k) = l*k и
и  как показано на рис. 1, достигается при
как показано на рис. 1, достигается при 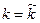 и, следовательно, значение
и, следовательно, значение  является корнем уравнения:
является корнем уравнения: (16)
(16) оказывает существенное влияние на вид переходных процессов в модели Солоу.
оказывает существенное влияние на вид переходных процессов в модели Солоу.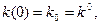 то она уже находится на стационарной траектории. В этом случае данную систему перевести в другое состояние можно только путем изменения значения одного из экзогенных показателей, например доли валовых инвестиций в валовом внутреннем продукте или, изменив производственную функцию, X(t)=F[K(t), L(t)].
то она уже находится на стационарной траектории. В этом случае данную систему перевести в другое состояние можно только путем изменения значения одного из экзогенных показателей, например доли валовых инвестиций в валовом внутреннем продукте или, изменив производственную функцию, X(t)=F[K(t), L(t)]. то в экономической системе происходит переходный процесс с выходом на стационарную траекторию, т.е.
то в экономической системе происходит переходный процесс с выходом на стационарную траекторию, т.е.  При этом наблюдаются три типа переходных процессов. Рассмотрим их применительно к изменению фондовооруженности труда во времени:
При этом наблюдаются три типа переходных процессов. Рассмотрим их применительно к изменению фондовооруженности труда во времени: то сначала происходит ускоренный рост фондовооруженности труда k(t), а затем, после достижения равенства
то сначала происходит ускоренный рост фондовооруженности труда k(t), а затем, после достижения равенства 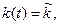 сменяется замедленным ростом данного показателя, с постепенным приближением к величине
сменяется замедленным ростом данного показателя, с постепенным приближением к величине  то наблюдается замедленный рост фондовооруженности труда k(t) к величине
то наблюдается замедленный рост фондовооруженности труда k(t) к величине  то происходит замедленное снижение фондовооруженности труда к величине
то происходит замедленное снижение фондовооруженности труда к величине 