 ПОЗНАВАТЕЛЬНОЕ
| Постановка задач и построение математической модели в абсолютных показателях
ВВЕДЕНИЕ Модель Харрода-Домара подверглась сильной критике, поскольку она имела следующие недостатки: 1. Модель предполагала, что рыночная экономика неустойчива. Необходимо соблюдать пропорции между инвестициями, накоплением и доходом. Если не соблюдать эти пропорции, то будет неустойчивый экономический рост: либо вверх, либо вниз. Хотя цель модели помочь развитым странам, но даже в развитых странах экономика неустойчива. Если «отпустить» экономику, то наступит экономический кризис. 2. Осуществили «большой толчок», а это не привело к ожидаемым результатам. Когда «проели» инвестиции, то снова наступил экономический кризис. Сформулированная Солоу в середине прошлого века концепция экономического роста привела к замене кейнсианской модели динамического развития экономики Харрода-Домара неоклассической теорией роста. При этом в исходной модели Солоу экономическая система рассматривается как единое целое, в которой производится один универсальный продукт. Этот продукт может потребляться и инвестироваться. Экспорт-импорт в явном виде не учитывается. Согласно модели Солоу рыночная экономика – устойчивая конструкция и самопроизводно стремится к устойчивому процессу. Отход от состояния равновесия включает силы, которые возвращают экономику в устойчивое состояние. Представленная работа состоит из двух разделов. В первом разделе делается постановка самой задачи. Во втором разделе рассматривается алгоритм вычисления показателей и дается экономический анализ полученных результатов. ПОСТАНОВКА ЗАДАЧИ Постановка задач и построение математической модели в абсолютных показателях Сформулированная Солоу в середине прошлого века концепция экономического роста привела к замене кейнсианской модели динамического развития экономики Харрода-Домара неоклассической теорией роста. При этом в исходной модели Солоу экономическая система рассматривается как единое целое, в которой производится один универсальный продукт. Этот продукт может потребляться и инвестироваться. Экспорт-импорт в явном виде не учитывается. Состояние экономической системы задается следующими эндогенными переменными: 1. Х(t) - валовой общественный продукт (ВОП); 2. С(t) - фонд непроизводственного потребления; 3. I(t) - валовые инвестиции в производственный капитал; 4. L(t) - число занятых в производственной деятельности; 5. К(t) - основные производственные фонды. Кроме того, состояние экономической системы определяется экзогенными (заданными извне) показателями: а) g - годовой темп прироста числа занятых в производственной б) m - доля основных производственных фондов, выбывших за в) а - доля промежуточного продукта в ВОП; г) Данные экзогенные показатели могут изменяться в следующих пределах: -1<g<1; 0<m<1; 0<a<1; 0< Годовой выпуск валового общественного продукта Х(t) в каждый момент времени t связан с ресурсами К(t) и L(t) посредством линейно-однородной неоклассической производственной функции: X(t) = F[K(t), L(t)]. (1) Сами ресурсные показатели, являясь эндогенными показателями, изменяются за небольшой промежуток времени 1. В соответствии с определением темп прироста числа занятых в производственной деятельности будет равен:
Разделив уравнение (2) на
или, при записи в стандартном виде:
Решение данного однородного линейного дифференциального уравнения L(t) = A*eg t (5) Используя начальное условие L(0)=L0, получим: L(t) = L0*eg t (6) 2. Прирост основных производственных фондов за промежуток времени
Если разделить уравнение (7) на
3. Функцию изменения валовых инвестиций во времени можно получить следующим образом:
где Y(t) - текущее значение валового внутреннего продукта, а Z(t) = a*X(t) - величина промежуточного продукта. 4. Величина фонда непроизводственного потребления, исходя из (9), находится по формуле:
Таким образом, получаем модель Солоу в абсолютных величинах в виде системы уравнений:
|



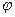 - доля валовых инвестиций в валовом внутреннем продукте
- доля валовых инвестиций в валовом внутреннем продукте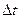 следующим образом:
следующим образом: . (2)
. (2) получим:
получим: , (3)
, (3) . (4)
. (4) . (7)
. (7) при
при  при K(0) = K0 (8)
при K(0) = K0 (8) (9)
(9) (10)
(10) (11)
(11)