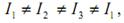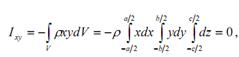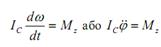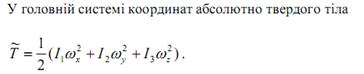ПОЗНАВАТЕЛЬНОЕ
| Відповіді до питань Механіки 12
Система відліку — це сукупність матеріальних точок, нерухомих одна відносно одної, відносно яких розглядається механічний рух, та годинників, що відлічують час. Для тривимірного простору достатньо 3 тіла, 2-вимірному 2 і т.д. Система відліку — це суто фізичне поняття, яке ґрунтується на виборі певних матеріальних об’єктів. Поняття системи координат - абстрактно-математичне. В одній і тій же фізичній системі відліку можна ввести безліч систем координат різних типів по-різному з нею пов’язаних, у тому числі і таких, що рухаються відносно системи відліку . З огляду на це немає жодних підстав для включення системи координат до означення системи відліку як це іноді трапляється. А система координат – це методика визначення положення тіла в даній системі відліку(не єдина). Принцип роботи GPS – вимірювання відстані до 4х штучних супутників Землі за часом. 4ий потрібний для підвищення точності.
Механічний Рух мат. точки — це переміщення мат. точки у фізичному середовищі відносно інших тіл або середовища. Існують три види опису мех. руху мат. точки: а) Векторний. Р-н траєкторії – це годограф б) Координатний. Положення м.т. задається 3 дійсними числами(її координатами), які є функцією часу. Тоді траєкторія описується системою р-н в) Природний. Коли траєкторія тіла наперед відома. Задається відстанню від вибраної точки відліку. Приклад – автомагістраль. Вектор переміщення( Шляхом(
Обертовий рух – це рух при якому всі точки тіла описують кола, центри яких лежить на 1 нерухомій прямій, яка називається віссю обертання. Три основні характеристики: вектор нескінченно малого повороту( Зв’язки між лінійними і кутовими величинами:
Поступальний рух – це рух, при якому будь-яка пряма , зв’язана з твердим тілом залишається паралельна своєму початковому напрямку. Довільне елементарне переміщення твердого тіла може бути представлене, як поступальний рух, при якому радіус-вектори всіх точок твердого тіла набувають однакових приростів, і обертовий, при якому відбувається нескінченно малий поворот твердого тіла. Тобто швидкість будь-якої точки тіла рівна – Частковим випадком руху твердого тіла є плоский рух(кожна точка твердого тіла рухається в площині, паралельній деякій нерухомій площині). Такий рух може бути описаний лише обертанням навколо так званої миттєвої осі обертання. Швидкість будь-якої точки тіла, що лежить на миттєвій осі обертання рівна нулю.
Для описання руху тіла потрібна якесь число n незалежних змінних, тоді кажуть, що це тіло має n ступенів вільності. Наприклад, для частинки у тривимірному просторі потрібно 3 незалежні змінні(координати), тобто частинка має 3 ступені вільності. Можливі випадки, коли рух є обмеженим по якомусь закону, тоді кажуть, що до тіла прикладені зв’язки. Наприклад, маленька кулька на стержні, має 2 ступені вільності, система з 2х жорстко зв’язаних кульок має 5 ступенів вільності. Оскільки положення абсолютно твердого тіла в просторі може бути задане положенням трьох його точок, які не лежать на 1 прямій, то при вільному русі тверде тіло має 6 ступенів вільності.
Інерціальна система відліку – це система відліку, вільний рух частинки в якій є рівномірним та прямолінійним. Або, ІСВ – це система відліку, прискорення частинки в якій повністю зумовлене взаємодією з іншими матеріальними об’єктами. Кожна система відліку, яка рухається рівномірно та прямолінійно відносно ІСВ є також ІСВ. З хорошою точністю ІСВ можна назвати геліоцентричну систему відліку, систему відліку пов’язану з центром галактики… Твердження про існування ІСВ і є основою 1 закону Ньютона: У ІСВ будь-яке тіло перебуває в стані спокою або рівномірного прямолінійного руху поки на нього не діють інші об’єкти.
Інертна маса – це скалярна фізична величина, яка є мірою інертності тіла. Де під інертністю, мається на увазі властивість тіла зберігати свій механічний стан. При швидкостях набагато менших швидкість світла маса має 2 такі властивості: а) Вона є адитивною(маса складеного тіла дорівнює сумі мас його складових) б) Не змінюється в процесі руху Другий закон Ньютона: Прискорення частинки в ІСВ прямо пропорційне прикладеній до неї силі, та обернено пропорційне її масі.
Існують 4 фундаментальні взаємодії: сильна, слабка, електромагнітна і гравітаційна, оскільки радіус дії у сильної та слабкої дуже малий(
Будь-яка дія одного тіла на інше носить характер взаємодії, причому сили з якими взаємодіють матеріальні точки одинакові за модулем, протилежні за напрямом і лежать на лінії, що їх з’єднує. Принцип відносності механіки(Галілея): Математичне формулювання законів механіки і властивості простору та часу не змінюються при переході з однієї ІСВ в іншу. Закони динаміки Ньютона справедливі в ІСВ, та при
Сили інерції в техніці та природі: 1) Відцентрова сила інерції: a. Відцентрові регулятори(регулятор Ватта, тощо) b. Центрифуги(сепаратори) 2) Поступальна сила інерції: a. Акселерометри 3) Сила Коріоліса a. Гіроскопи b. Відхилення падаючих тіл на схід c. Підмивання берегів річок, що течуть в меридіональному напрямку. d. Напрямки обертання циклонів та антициклонів.
Сила, яка діє на тіло поблизу поверхні Землі, не зважаючи на те рухається тіло чи ні називається силою тяжіння Землі:
Вага тіла – це сила з якою воно діє на зв’язки. Невагомість, стан в якому Вага тіла = 0. Перевантаженням називають стан, коли вага тіла більша за його "нормальну" вагу(mg). В орбітальній станції брати НеІСВ, пов'язану з центром в ц. мас станції, тоді
Відхилення падаючих тіл на схід
Спостерігач, який знаходиться в аудиторії, ясно бачить, що коливання маятника відбуваються в площині, положення якої залишається незмінним відносно лабораторного стола і стін лабораторії, тобто відносно земної поверхні, яку в умовах цього досліду можна вважати інерціальною системою відліку, оскільки кутова швидкість обертання Землі більш як на п’ять порядків менша за обрану кутову швидкість обертання диска. Але відносно диска (для спостерігача, який “перебуває” на диску) площина коливань маятника повертається з кутовою швидкістю, рівною кутовій швидкості обертання диска відносно ICB. Таким чином, з точки зору ICB ситуація гранично проста: на кульку маятника діють лише дві сили: сила тяжіння g mr та сила натягу нитки Tr, площина коливань визначається початковими умовами і її положення не змінюється в процесі руху, а диск просто “прокручується” під маятником. Однак при спостереженні руху величезного маятника з довжиною підвісу 67 м підвішеного Фуко під куполом величної будівлі Пантеону в Парижі, площина коливань якого повертається відносно стін буквально на очах, відвідувачам важко відмовитись від враження, що на маятник діє якась таємнича сила в бічному напрямі. Настільки ж важко для спостерігача, що знаходиться всередені будівлі, уявити обертання цієї будівлі разом із ділянкою поверхні Землі, на якій вона стоїть, відносно якоїсь невидимої інерціальної системи відліку! Давно помічено, що ріки північної півкулі, що течуть у меридіональному напрямку, мають правий берег більш крутий та розмитий. Прикладом може бути Дніпро. У південній півкулі, навпаки, більш круті і розмиті ліві береги, а більш пологі – праві. У південній півкулі напрями закручування вихорів у циклонах та антициклонах є протилежні відповідним напрямам у північній півкулі.
3 Закони Ньютона дають нам можливість взнати механічний стан частинки в будь-який момент часу, якщо ми знаємо сили, які до неї прикладені, а також початкові умови(початковий механічний стан). Якщо ж розглядати систему частинок, то знаючи для кожної з них прикладені сили, а також початкові умови, попри всі математичні складності, ми можемо знайти характеристику руху кожної ОКРЕМОЇ частинки, а не системи в цілому. Тому постає необхідність знайти такі величини, які б характеризували механічний стан системи в цілому через характеристики механічного стану її частинок і при цьому не залежали б у явному вигляді від механічного стану кожної окремої частинки. Система частинок називається замкненою, якщо на її частинки не діють сили з боку матеріальних об’єктів, що не належать до цієї системи. Сили, що прикладені до частинок системи, можна поділити на так звані внутрішні(сили взаємодії між частинками самої системи) і зовнішні(сили взаємодії частинок системи з матеріальними об’єктами, що не належать до системи).
Векторну величину
Отже, Імпульс частинки змінюється, під дією прикладених до неї сил(якщо їхня сума не рівна 0). Умова збереження імпульсу частинки: Імпульс частинки зберігається, якщо сума сил прикладених до частинки рівна нулю. Якщо якась компонента суми сил прикладених до частинки рівна нулю, то відповідна компонента вектора імпульсу частинки зберігається.
Імпульс системи частинок:
Імпульс системи частинок змінюється під дією зовнішніх сил, якщо їх сума не дорівнює 0. Імпульс системи зберігається, якщо сума всіх зовнішніх сил, прикладених до частинок системи, дорівнює 0. ЗЗІСЧ: Імпульс замкненої системи частинок зберігається. Якщо якась компонента суми зовнішніх сил рівна нулю, то відповідна компонента імпульсу системи частинок зберігається.
Центр мас системи частинок, це точка радіус вектор якої задається рівнянням:
Тоді Система центру мас – це система відліку, в якій центр мас залишається в спокої. Тобто,
Розглянемо найбільш загальний випадок, коли має місце одночасне приєднання та від'єднання мас з ненульовими швидкостями відносно тіла змінної маси.
Реактивний рух літака:
Реактивний рух ракети:
Формула Цілковського
Векторну величину
Векторну величину Умова збереження моменту імпульсу частинки: Момент імпульсу частинки зберігається, якщо момент суми сил прикладених до частинки дорівнює 0. Якщо якась компонента моменту суми сил дорівнює нулю, то відповідна компонента моменту імпульсу частинки зберігається.
Момент імпульсу системи частинок:
Момент імпульсу системи частинок змінюється, якщо зовнішні сили створюють не нульовий момент сил, прикладений до частинок системи. Момент імпульсу системи частинок зберігається, якщо сумарний момент зовнішніх сил, прикладений до частинок системи рівний нулю. ЗЗМІСЧ: Моменті імпульсу замкненої системи частинок зберігається.
Власний момент імпульсу системи частинок – це момент імпульсу визначений в системі ЦМ. Розглянемо момент імпульсу системи частинок визначений відносно двох різних точок:
Р=0, в системі центра мас, тобто власний момент імпульсу не залежить від точки відносно якої його визначати. Зв'язок між вільним та визначеним в довільній ІСВ моментом імпульсу системи частинок:
Скалярна величина
Скалярну величину Умова збереження кінетичної енергії частинки: Кінетична енергія частинки зберігається, якщо сумарна потужність прикладених до неї сил дорівнює нулю. Величину
Потенціальне поле сил – це стаціонарне силове поле(сила прикладена до частинки в кожній точці силового поля не змінюється з часом) в якому робота по переміщенню частинки між двома довільними точками не залежить від форми траєкторії, а лише від положення цих точок.(Гравітаційне поле, Електростатичне поле точкового заряду, квазіпружнє силове поле) Розглянемо роботу по переміщенню з будь-якої точки P в фіксовану точку О, тоді Робота ж по переміщенню частинки з однієї точки в іншу:
В будь-якій точці потенціального силового поля на частинку діє сила, що рівна градієнту потенціальної енергії в цій точці.
Повна механічна енергія частинки – це сума кінетичної та потенціальної енергії частинки.
Сили можна поділити на консервативні(сили потенціального силового поля) та неконсервативні(сторонні), тоді
Повна мех.. енергія змінюється при наявності відмінної від нуля сумарної потужності сторонніх сил. Умова збереження повної мех.. енергії: ПМЕ зберігається, якщо сумарна потужність сторонніх сил дорівнює нулю.
Елементарний приріст енергії системи частинок:
Величина
Величину Повна механічна енергія системи частинок змінюється за рахунок відмінних від нуля суми роботи зовнішніх та внутрішніх неконсервативних сил. Повна механічна енергія системи частинок зберігається, якщо сума робіт зовнішніх та внутрішніх неконсервативних сил рівна нулю. Закон збереження повної механічної енергії замкненої системи частинок: Повна механічна енергія замкненої системи частинок, між якими діють лише консервативні сили, зберігається. З внутрішніх неконсервативних(сторонніх) сил можна виділити такі, робота яких завжди менша нуля, їх називають дисипативними.
U – внутрішня(власна) потенціальна енергія системи частинок U' – потенціальна енергія системи частинок у зовнішньому потенціальному силовому полі. (При відсутності внутрішніх дисипативних сил) Зберігається, якщо зовнішнє потенціальне поле стаціонарне та потужність зовнішніх неконсервативних сил дорівнює нулю.
При одновимірному русі механічний стан частинки визначається лише однією змінною (координатою) , що залежить від часу. При відсутності дисипативних сил, енергія такої частинки може бути подана таким р-н:
Механічний рух частинки дозволений лише в тому місці, де Інфінітний – це рух при тіло може прямувати на нескінченність(рух не обмежений). Фінітний – це рух при якому тіло не виходить за межі певних
Вважаємо x0 початком відліку і отримуємо:
33. Застосування законів збереження до аналізу руху частинки в полі центральної сили: загальні характеристики руху та траєкторії, умова замкненості траєкторії.
Момент імпульсу частинки в полі центральної сили, визначений відносно центра поля зберігається:
ϕ0 позначено сталу інтегрування. Таким чином, ми отримали залежить від конкретного виду потенціальної енергії
Таким чином, траєкторія частинки буде замкненою, якщо відношення
34. Зіткнення частинок. Пружні та непружні зіткнення. Аналіз лобових абсолютно пружних та абсолютно непружних зіткнень. Під зіткненням двох частинок розуміють такий процес, що відбувається за відсутності впливу інших матеріальних об’єктів, результатом якого є зміна початкових швидкостей частинок, які вони мали перебуваючи на великій відстані одна від одної, внаслідок взаємодії частинок між собою. Розрізняють так звані абсолютно пружні зіткнення, при яких зберігається повна механічна енергія E системи двох частинок, тобто повна механічна енергія системи після зіткнення E′ дорівнює повній механічній енергії до зіткнення, E ′ = E, та непружні зіткнення, внаслідок яких повна механічна енергія зменшується, E′ < E . Граничним випадком непружного зіткнення є абсолютно непружне зіткнення, при якому частинки не «відскакують» одна від одної, а після якого рухаються разом. Найпростішим є випадок так званих лобових зіткнень, коли до і після зіткнення обидві частинки рухаються по траєкторіям, що повністю лежать на одній прямій. Розглянемо спочатку випадок абсолютно непружного лобового зіткнення Скористаємося законом збереження імпульса у формі де враховано, що за означенням абсолютно непружного зіткнення обидві частинки після зіткнення рухаються разом, тобто з однаковою швидкістю υ′, яку знаходимо з Легко бачити, що знайдена швидкість дорівнює швидкості центру мас системи , яка для замкненої системи частинок є сталою. Це є відображенням того простого факту, що після абсолютно непружного зіткнення внутрішній рух системи частинок припинився. Повні механічні енергії системи двох частинок до і після зіткнення є, відповідно,
35. Застосування законів збереження імпульсу та енергії до абсолютно пружного зіткнення двох частинок. Діаграма імпульсів. Для випадку абсолютно пружного лобового зіткнення використаємо як закон збереження імпульса так і закон збереження енергії Оскільки рух обох частинок відбувається вздовж однієї прямої, спроектуємо рівняння (● на напрям швидкості першої частинки
36. Зв’язок між законами збереження та фундаментальними властивостями простору і часу.
37. Рух абсолютно твердого тіла як поступальний рух центру мас та обертання навколо осі, що проходить через центр мас. Як відзначалося раніше, абсолютно тверде тіло можна означити як систему частинок нерухомих одна відносно одної в процесі руху цієї системи. Отже, для твердого тіла як для всякої системи частинок можна записати два векторних рівняння, а саме рівняння руху системи як цілого під дією зовнішніх сил для проекцій, що відповідає шести ступеням свободи абсолютно твердого тіла, серед яки є три поступальних і три обертальних. При цьому рівняння (6._1) описує поступальний рух абсолютного твердого тіла. Його можна подати у вигляді рівняння руху центру мас абсолютного твердого тіла
38. Рівняння руху твердого тіла. Про можливість введення рівнодіючої сили.
тіла, що лежить на прямій, що проходить на відстані від центру мас тіла C в площині, в якій лежить центр мас тіла і яка перпендикулярна моменту зовнішніх сил
39. Умови рівноваги твердого тіла. Приклад: рівновага балки. Необхідність врахування деформацій в невизначено-статичних задачах. Для абсолютно твердого тіла, що знаходилося в рівновазі, тобто не рухається, виконуються умови
40. Зв’язок між вектором момента імпульса і вектором кутової швидкості абсолютно твердого тіла. Тензор інерції.
Тензором інерції називається тензорна фізична величина, що характеризує інерційні властивості твердого тіла щодо обертання, і яка в кожній системі координат визначається дев’ятьма скалярними величинами (компонентами тензора інерції або моментами інерції твердого тіла), які залежать від розподілу мас у твердому тілі і в кожній декартовій системі координат визначаються формулою
41. Основні властивості тензора інерції та обчислення його компонент. Приклад обчислення компонент тензора інерції однорідного прямого паралeлепіпеда. 1. Якщо всі три головні моменти інерції абсолютно твердого тіла різні, тобто то про таке тіло кажуть, що воно за своїми інерційними властивостями щодо обертання являє собою несиметричну дзигу;
42. Обертання твердого тіла навколо нерухомої осі. Момент інерції тіла відносно осі обертання.Теорема Гюйгенса-Штейнера. Оскільки єдиною характеристикою такого руху є вектор кутової швидкості ω r, який направлений вздовж осі обертання, будемо спочатку вважати, що вісь обертання проходить через центр мас твердого тіла .
Гюйгенса-Штейнера: момент інерції твердого тіла відносно довільної осі є сума момента інерції тіла відносно паралельної осі, що проходить через центр мас тіла, та добутка маси тіла на квадрат відстані між цими осями.
45. Кінетична енергія абсолютно твердого тіла, її вираз через компоненти тензора інерції та вектора кутової швидкості.
46. Обертання твердого тіла навколо нерухомої осі. Оскільки єдиною характеристикою такого руху є вектор кутової швидкості ω r, який направлений вздовж осі обертання, будемо спочатку вважати, що вісь обертання проходить через центр мас твердого тіла .
47. Плоский рух твердого тіла, Задача про скочування циліндра з похилої площини. Рух колеса воза і колеса автомобіля.
48. Рух твердого тіла з однією нерухомою точкою ( гіроскопи ). Прецесія осі гіроскопа. Гіроскопом називають масивне симетричне тіло, що обертається з великою кутовою швидкістю навколо своєї осі симетрії. Прикладом гіроскопа може бути дітяча дзига. Якщо намагатися поставити її вертикально без обертання, то вона відразу впаде. Якщо ж їй надати швидкого обертання навколо осі симетрії і обережно поставити на горизонтальну поверхню, так щоб напрям її осі був близьким до вертикалі, то вона здатна тривалий час зберігати цей напрям. При цьому можна помітити, що вісь дзиги описує конус навколо вертикалі, причому дзига не падає навіть при значному відхиленні від вертикалі, якщо кутова швидкість ω її обертання навколо власної осі симетрії достатньо велика. Це явище називають прецесією осі гіроскопа. Чим більша швидкість ω , тим менша кутова швидкість прецесії Ω, з якою вісь дзиги описує конус навколо вертикалі. Швидкість ω поступово зменшується внаслідок втрати енергії за рахунок роботи дисипативних сил тертя в точці опори і опору повітря: при цьому збільшується Ω і кут відхилення від вертикалі і дзига врешті решт падає.
49. Виникнення гіроскопічних сил, застосування гіроскопів. Відповідно до третього закону Ньютона Виникнення гіроскопічних сил при спробі змінити напрям осі обертання гіроскорпа називають гіроскопічним ефектом. Гіроскопічний ефект має місце при поворотах різних машин і механізмів, що містять частини, які швидко обертаються: вали двигунів, трансмісій, ротори електродвигунів, турбін тощо. Найбільше він виявляється у транспортних засобах, які можуть мати значну кутову швидкість при поворотах: підшипники валу турбіни на кораблі або газової турбіни і компресора в турбореактивному двигуні літака зазнають значних навантажень при маневрах. Дія гіростабілізаторів здебільше ґрунтується на властивості тристепеневого гіроскопа зберігати незмінним напрям своєї осі обертання. При цьому можуть використовуватись як безпосереднью гіроскопічні моменти важкого масивного гіроскопа, як наприклад, в деяких заспокоювачах качки, і порівняно невеликий і легкий гіроскоп як датчик напрямку, що виробляє сигнали для керування силовими пристроями, які забезпечують стабілізіцію орієнтації платформи або якогось пристрою в просторі.
12 |



 , який відкладається від деякої точки О, нерухомої відносно системи відліку.
, який відкладається від деякої точки О, нерухомої відносно системи відліку. . Зв'язок між векторним та координатним способами:
. Зв'язок між векторним та координатним способами: 
 ) – цевектор, початок якого співпадає з початковим положенням частинки, а кінець — з її кінцевим положенням.
) – цевектор, початок якого співпадає з початковим положенням частинки, а кінець — з її кінцевим положенням.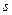 ) називається довжина дуги траєкторії, що з’єднує початкове та кінцеве положення частинки.
) називається довжина дуги траєкторії, що з’єднує початкове та кінцеве положення частинки.
 , де
, де 
 ), вектор кутової швидкості(
), вектор кутової швидкості(  ) та вектор кутового прискорення(
) та вектор кутового прискорення(  ). Вони є аксіальними(псевдовекторами). Формула додавання нескінченно малих кутів повороту:
). Вони є аксіальними(псевдовекторами). Формула додавання нескінченно малих кутів повороту:  , та кутових швидкостей:
, та кутових швидкостей: 

 , де кутова швидкість
, де кутова швидкість  -- єдина(абсолютна) характеристика обертового руху, і вона не залежить від вибору осі обертання.
-- єдина(абсолютна) характеристика обертового руху, і вона не залежить від вибору осі обертання. ), то актуальними в механіці є електромагнітна та гравітаційна.
), то актуальними в механіці є електромагнітна та гравітаційна.


 .
.





 називають імпульсом частинки. Імпульс вільної частинки є величина стала.
називають імпульсом частинки. Імпульс вільної частинки є величина стала.
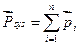

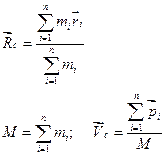
 називається рівнянням руху центру мас.
називається рівнянням руху центру мас. , а це і означає, що в СЦМ імпульс системи частинок рівний нулю.
, а це і означає, що в СЦМ імпульс системи частинок рівний нулю.


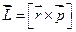 називають моментом імпульсу частинки. Момент імпульсу вільної частинки є величина стала.
називають моментом імпульсу частинки. Момент імпульсу вільної частинки є величина стала.
 називають моментом сили. Отже, момент імпульсу частинки змінюється під дією моменту суми сил, прикладених до частинки(якщо він не рівний 0)
називають моментом сили. Отже, момент імпульсу частинки змінюється під дією моменту суми сил, прикладених до частинки(якщо він не рівний 0)



 називається кінетичною енергією частинки. Кінетична енергія вільної частинки є величина стала.
називається кінетичною енергією частинки. Кінетична енергія вільної частинки є величина стала.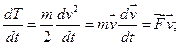
 називають потужністю. Отже, кінетична енергія частинки змінюється під дією не нульової сумарної потужності сил.
називають потужністю. Отже, кінетична енергія частинки змінюється під дією не нульової сумарної потужності сил. називають елементарною роботою.
називають елементарною роботою. , тобто зміна кінетичної енергію частинки дорівнює сумарній роботі сил прикладених до частинки.
, тобто зміна кінетичної енергію частинки дорівнює сумарній роботі сил прикладених до частинки. називається потенціальною енергією. Потенціальна енергія залежить від вибору точки О.
називається потенціальною енергією. Потенціальна енергія залежить від вибору точки О. при чому різниця
при чому різниця  та
та  не залежить від вибору точки О.
не залежить від вибору точки О.
 ПМЕ частинки, на яку не діють сторонні сили, зберігається.
ПМЕ частинки, на яку не діють сторонні сили, зберігається.

 називається внутрішньою потенціальною енергією системи частинок
називається внутрішньою потенціальною енергією системи частинок
 називають повною механічною енергією системи частинок.
називають повною механічною енергією системи частинок. , де Т – кінетична енергія системи частинок
, де Т – кінетична енергія системи частинок
 , область, де
, область, де  є класично недосяжною.
є класично недосяжною. та
та  .
.

 , оскільки U(x) розглядається поблизу екстремуму. Тому функція набуває вигляду:
, оскільки U(x) розглядається поблизу екстремуму. Тому функція набуває вигляду: . Іншими доданками нехтуємо, оскільки коливання малі.
. Іншими доданками нехтуємо, оскільки коливання малі. , де введено позначення
, де введено позначення  . Тоді на частинку діє сила
. Тоді на частинку діє сила  . Це рух під дією квазипружної сили, звідки його період:
. Це рух під дією квазипружної сили, звідки його період:



 де через
де через , тобто рівняння траєкторії у явному вигляді, що
, тобто рівняння траєкторії у явному вигляді, що . Ясно, що при наявності залежності
. Ясно, що при наявності залежності можна, в принципі, знайти й обернену залежність
можна, в принципі, знайти й обернену залежність  .
. є раціональне число.
є раціональне число.



 Отже, маємо систему двох рівнянь з двома невідомими 1 υ′ та 2 υ′ . Перепишемо рівняння (●● та (● у вигляді
Отже, маємо систему двох рівнянь з двома невідомими 1 υ′ та 2 υ′ . Перепишемо рівняння (●● та (● у вигляді 

 Дійсно, два векторних рівняння (6._1) та (6._2) еквівалентні шести скалярним рівнянням
Дійсно, два векторних рівняння (6._1) та (6._2) еквівалентні шести скалярним рівнянням
 Отже,
Отже,  , то систему сил, що прикладені до окремих певних точок абсолютно твердого тіла, можна замінити так званою рівнодіючою силою, яка дорівнює результуючій силі
, то систему сил, що прикладені до окремих певних точок абсолютно твердого тіла, можна замінити так званою рівнодіючою силою, яка дорівнює результуючій силі , причому рівнодіюча сила може бути прикладена до будь-якої точки твердого
, причому рівнодіюча сила може бути прикладена до будь-якої точки твердого

 Ці умови є необхідними, але недостатніми для того, щоб тіло знаходилось у рівновазі, оскільки вони припускають рівномірний рух центру мас і рівномірне обертання тіла навколо осі, що проходить через його центр мас. Їх треба доповнити відповідними початковими умовами
Ці умови є необхідними, але недостатніми для того, щоб тіло знаходилось у рівновазі, оскільки вони припускають рівномірний рух центру мас і рівномірне обертання тіла навколо осі, що проходить через його центр мас. Їх треба доповнити відповідними початковими умовами