 ПОЗНАВАТЕЛЬНОЕ
| Гирю взвесили на образцовых весах и получили ее действительное значение, равное 1,980 кг. 12
Решение Более точным будем считать измерение погрешность которого имеет меньшее значение. Погрешность измерения первым амперметров определяется по классу точности (ГОСТ 8.401-80), если класс точности СИ представлен в виде
где Отсюда определяем абсолютную погрешность измерения первым амперметром:
Для второго амперметра, класс точности записан в виде 1,5, что является значением приведенной погрешности (ГОСТ 8.401-80):
где Отсюда, определим абсолютную погрешность измерения:
Т.о. более точным будет измерение, проведенное с помощью первого амперметра.
№ 2 Дан ряд измерений (мм): 50,04; 50,02; 50,08; 50,01; 50,03; 50,04; 50,04; 50,02; 50,05; 50,04. Какую погрешность дает однократное измерение? Достаточно ли измерений, чтобы найти диаметр с погрешностью +0,05 мм, Решение За результат однократного измерения принимается значение величины, полученное при измерении после исключения систематической погрешности. Погрешность одного измерения (не входящего в ряд; измерений), оценивается на основании известных погрешностей средства и метода измерений в данных условиях (измерений). Результат однократного измерения представляется в виде:
где величина Оценка погрешности результата вычисляется предварительно по известным оценкам составляющих погрешности. На практике для оценки погрешности однократного прямого измерения пользуются приближенными методами, т.е. речь идет о приближенном оценивании погрешности результата на основе заранее известных основной и дополнительной погрешности, указанной в паспорте прибора. Погрешность многократных измерений оцениваются с учетом рекомендаций ГОСТ Р 8.736-2011. При нормальном законе распределения погрешности
Для нашей задачи:
Абсолютную погрешность каждого из
Алгебраическая сумма случайных отклонений отдельных наблюдений от среднего арифметического значения при достаточно большом числе измерений равна нулю:
Далее определяется оценка среднеквадратичного отклонения
Оценка характеризует степень разброса значений
На практике для оценки точности и надежности полученных результатов пользуются доверительной вероятностью и доверительным интервалом. Под доверительной вероятностью При поиске доверительного интервала вероятность
Значения коэффициентов
Т.к. данное значение
№ 3 Требуется измерить температуру, равную Для измерения выбран пирометрический милливольтметр с диапазоном Решение Воспользуемся положениями ГОСТ 8.401-80 и на основе класса точности представленного милливольтметра определим абсолютную погрешность измерения температуры данным прибором. Т.к. класс точности равен приведенной погрешности:
запишем для абсолютной погрешности:
Зная абсолютную погрешность воспользуемся известной формулой и определим относительную погрешность измерения температуры:
Т.к. полученное значение относительной погрешности измерения температуры
№ 4 С помощью гири 2 кг производится расфасовка товара. Фасовать товар требуется с погрешностью не более 2 %. Гирю взвесили на образцовых весах и получили ее действительное значение, равное 1,980 кг. 12 |



 , то онявляется относительной погрешностью измерения:
, то онявляется относительной погрешностью измерения: ,
, - абсолютная погрешность измерения;
- абсолютная погрешность измерения;  - значение измеренной величины.
- значение измеренной величины. .
. ,
,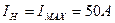 - нормированное значение, для амперметра оно соответствует верхнему пределу измерения.
- нормированное значение, для амперметра оно соответствует верхнему пределу измерения. .
.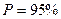
 ,
, представляет собой приборную погрешность.
представляет собой приборную погрешность. за истинную величину
за истинную величину  принимают ее оптимальную оценку
принимают ее оптимальную оценку  в виде среднего арифметического значения (оценки математического ожидания) выполненного ряда наблюдений:
в виде среднего арифметического значения (оценки математического ожидания) выполненного ряда наблюдений: .
. .
. наблюдений вычисляют:
наблюдений вычисляют: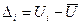
 .
. наблюдений, характеризующая точность метода измерений:
наблюдений, характеризующая точность метода измерений: .
. .
. понимается вероятность появления погрешности, не выходящей за некоторые принятые границы. Этот интервал называется доверительным интервалом, а характеризующая его вероятность — доверительной вероятностью.
понимается вероятность появления погрешности, не выходящей за некоторые принятые границы. Этот интервал называется доверительным интервалом, а характеризующая его вероятность — доверительной вероятностью. . Если число наблюдений
. Если число наблюдений  , то для расчета доверительной границы
, то для расчета доверительной границы 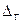 можно использовать распределение Стьюдента, учитывающее число «
можно использовать распределение Стьюдента, учитывающее число « 
 этого распределения приведены в Приложении Д ГОСТ Р 8.736-2011, тогда:
этого распределения приведены в Приложении Д ГОСТ Р 8.736-2011, тогда: .
. меньше заявленного +0,05 мм, т.о. 10-ти кратное количество измерений обеспечивает заявленную точность с вероятностью
меньше заявленного +0,05 мм, т.о. 10-ти кратное количество измерений обеспечивает заявленную точность с вероятностью  с погрешностью не более 3 %.
с погрешностью не более 3 %. класса точности 1,5. Обеспечит ли выбранный прибор выполнение требований задачи?
класса точности 1,5. Обеспечит ли выбранный прибор выполнение требований задачи? ,
,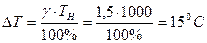 .
.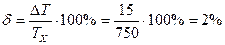 .
. не превосходит 3%, то можно сделать вывод о том, что данный милливольтметр может быть использован для проведения измерения температуры с заявленной и точностью.
не превосходит 3%, то можно сделать вывод о том, что данный милливольтметр может быть использован для проведения измерения температуры с заявленной и точностью.