Задания для самостоятельной работы
Вариант 1. 1. Убедиться, что векторы  образуют подгруппу относительно сложения в группе образуют подгруппу относительно сложения в группе  всех векторов с координатами из всех векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а) 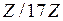 ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с  соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  ; б) ; б)  . . 5. Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 2. 1. Убедиться, что векторы  образуют подгруппу относительно сложения в группе образуют подгруппу относительно сложения в группе  всех пятимерных векторов с координатами из всех пятимерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а)  ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с  соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а) 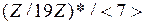 ; б) ; б)  . . 5. Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 3. 1. Убедиться, что векторы  образуют подгруппу относительно сложения в группе образуют подгруппу относительно сложения в группе  всех векторов с координатами из всех векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а)  ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с  соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  ; б) ; б)  . . 5.Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 4. 1. Убедиться, что векторы  образуют подгруппу относительно сложения в группе образуют подгруппу относительно сложения в группе  всех пятимерных векторов с координатами из всех пятимерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а)  ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с  и и  соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  б) б)  5. Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 5. 1. Выписать все элементы подгруппы, порожденной векторами  аддитивной группе аддитивной группе  5-мерных векторов с координатами из 5-мерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а)  ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с  и и  соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  ; б) ; б) 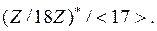 5. Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 6. 1. Выписать все элементы подгруппы, порожденной векторами  в аддитивной группе в аддитивной группе  5-мерных векторов с координатами из 5-мерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а)  ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с  и и 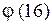 соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  ; б) ; б)  5. Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 7. 1. Выписать все элементы подгруппы, порожденной векторами  в аддитивной группе в аддитивной группе  5-мерных векторов с координатами из 5-мерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а) 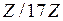 ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с  и и  соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  ; б) ; б) 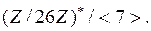 5. Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 8. 1. Выписать все элементы подгруппы, порожденной векторы  в аддитивной группе в аддитивной группе  5-мерных векторов с координатами из 5-мерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а)  ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с  и и  соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  ; б) ; б)  5.Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 9. 1. Выписать все элементы подгруппы, порожденной векторами  в аддитивной группе в аддитивной группе  5-мерных векторов с координатами из 5-мерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а)  ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с   и и   соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  ; б) ; б)  5. Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 10. 1. Выписать все элементы подгруппы, порожденной векторами  в аддитивной группе в аддитивной группе  5-мерных векторов с координатами из 5-мерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а)  ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с  и и  соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  ; б) ; б)  5. Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 11. 1. Выписать все элементы подгруппы, порожденной векторами  в аддитивной группе в аддитивной группе  5-мерных векторов с координатами из 5-мерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а)  ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с  и и  соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  ; б) ; б)  5. Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 12. 1. Выписать все элементы подгруппы, порожденной векторами  в аддитивной группе в аддитивной группе  5-мерных векторов с координатами из 5-мерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а) 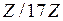 ; б) ; б)  . Сравнить количество этих элементов с . Сравнить количество этих элементов с  и и 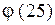 соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  ; б) ; б)  5.Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 13. 1. Убедиться, что векторы  образуют подгруппу относительно сложения в группе образуют подгруппу относительно сложения в группе  всех пятимерных векторов с координатами из всех пятимерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца: а) 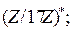 б) б)  Сравнить количество этих элементов с Сравнить количество этих элементов с  и и  соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а) 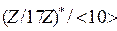 ; б) ; б)  5.Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 14. 1. Убедиться, что векторы  образуют подгруппу относительно сложения в группе образуют подгруппу относительно сложения в группе  всех 5-мерных векторов с координатами из всех 5-мерных векторов с координатами из  2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца:
а)  б) б)  Сравнить количество этих элементов с Сравнить количество этих элементов с 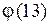 и и  соответственно. Является ли эта группа относительно умножения соответственно. Является ли эта группа относительно умножения
циклической? 4. Выписать таблицу смежных классов: а)  б) б)  5. Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3. Вариант 15. 1. Убедиться, что векторы  образуют подгруппу относительно сложения в группе образуют подгруппу относительно сложения в группе  всех 5-мерных векторов с координатами из всех 5-мерных векторов с координатами из  . . 2. Выписать таблицу смежных классов группы  по данной подгруппе. по данной подгруппе. 3. Выписать все элементы мультипликативной группы кольца:
а)  б) б)  Сравнить количество этих элементов с Сравнить количество этих элементов с  и и  соответственно. Является ли эта группа относительно умножения циклической? соответственно. Является ли эта группа относительно умножения циклической? 4. Выписать таблицу смежных классов: а)  б) б)  5. Содержит ли группа  нециклическую подгруппу? нециклическую подгруппу? 6. Является ли нормальной подгруппа  в группе в группе  для подстановки для подстановки  из задания 2 с лабораторной работы № 3. из задания 2 с лабораторной работы № 3.
| 



 образуют подгруппу относительно сложения в группе
образуют подгруппу относительно сложения в группе  всех векторов с координатами из
всех векторов с координатами из 
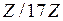 ; б)
; б)  . Сравнить количество этих элементов с
. Сравнить количество этих элементов с  соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической? ; б)
; б)  .
. в группе
в группе  для подстановки
для подстановки  из задания 2 с лабораторной работы № 3.
из задания 2 с лабораторной работы № 3. образуют подгруппу относительно сложения в группе
образуют подгруппу относительно сложения в группе  ; б)
; б)  . Сравнить количество этих элементов с
. Сравнить количество этих элементов с  соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической?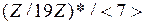 ; б)
; б)  .
. нециклическую подгруппу?
нециклическую подгруппу? для подстановки
для подстановки  образуют подгруппу относительно сложения в группе
образуют подгруппу относительно сложения в группе  ; б)
; б)  . Сравнить количество этих элементов с
. Сравнить количество этих элементов с  соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической? ; б)
; б)  .
. нециклическую подгруппу?
нециклическую подгруппу? образуют подгруппу относительно сложения в группе
образуют подгруппу относительно сложения в группе 
 ; б)
; б)  . Сравнить количество этих элементов с
. Сравнить количество этих элементов с  и
и  соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической? б)
б) 
 нециклическую подгруппу?
нециклическую подгруппу? аддитивной группе
аддитивной группе 
 ; б)
; б)  . Сравнить количество этих элементов с
. Сравнить количество этих элементов с  и
и  соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической? ; б)
; б) 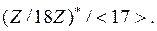
 нециклическую подгруппу?
нециклическую подгруппу? в аддитивной группе
в аддитивной группе 
 ; б)
; б)  . Сравнить количество этих элементов с
. Сравнить количество этих элементов с  и
и 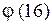 соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической? ; б)
; б) 
 нециклическую подгруппу?
нециклическую подгруппу? . Сравнить количество этих элементов с
. Сравнить количество этих элементов с  и
и  соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической? ; б)
; б) 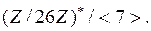
 нециклическую подгруппу?
нециклическую подгруппу? в аддитивной группе
в аддитивной группе  ; б)
; б)  . Сравнить количество этих элементов с
. Сравнить количество этих элементов с  и
и  соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической? ; б)
; б) 
 нециклическую подгруппу?
нециклическую подгруппу? . Сравнить количество этих элементов с
. Сравнить количество этих элементов с  и
и  ; б)
; б) 
 нециклическую подгруппу?
нециклическую подгруппу? в аддитивной группе
в аддитивной группе  . Сравнить количество этих элементов с
. Сравнить количество этих элементов с  соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической? ; б)
; б) 
 нециклическую подгруппу?
нециклическую подгруппу? в аддитивной группе
в аддитивной группе  ; б)
; б)  . Сравнить количество этих элементов с
. Сравнить количество этих элементов с  и
и  соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической? ; б)
; б) 
 нециклическую подгруппу?
нециклическую подгруппу? в аддитивной группе
в аддитивной группе 
 по данной подгруппе.
по данной подгруппе. . Сравнить количество этих элементов с
. Сравнить количество этих элементов с 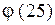 соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической? ; б)
; б) 
 нециклическую подгруппу?
нециклическую подгруппу? в группе
в группе  образуют подгруппу относительно сложения в группе
образуют подгруппу относительно сложения в группе 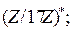 б)
б)  Сравнить количество этих элементов с
Сравнить количество этих элементов с  и
и  соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической?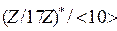 ; б)
; б) 
 нециклическую подгруппу?
нециклическую подгруппу? в группе
в группе  образуют подгруппу относительно сложения в группе
образуют подгруппу относительно сложения в группе 
 б)
б)  Сравнить количество этих элементов с
Сравнить количество этих элементов с 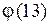 и
и  соответственно. Является ли эта группа относительно умножения
соответственно. Является ли эта группа относительно умножения б)
б) 
 нециклическую подгруппу?
нециклическую подгруппу? образуют подгруппу относительно сложения в группе
образуют подгруппу относительно сложения в группе  .
. б)
б)  Сравнить количество этих элементов с
Сравнить количество этих элементов с  и
и  соответственно. Является ли эта группа относительно умножения циклической?
соответственно. Является ли эта группа относительно умножения циклической? б)
б) 
 нециклическую подгруппу?
нециклическую подгруппу?