Задания для аудиторной работы
Подгруппы Теоретические сведения Определение 4.1.Подгруппой в группе  называется всякое непустое подмножество называется всякое непустое подмножество  элементов множества элементов множества  , которое в свою очередь является группой относительно той же операции. Подгруппа , которое в свою очередь является группой относительно той же операции. Подгруппа  группы группы  называется собственной, если называется собственной, если  и и 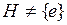 . . Выяснить, какое из подмножеств группы является подгруппой помогает Теорема 4.1 (Критерий подгруппы). Непустое подмножество  группы группы  является подгруппой тогда и только тогда, когда для произвольных элементов является подгруппой тогда и только тогда, когда для произвольных элементов 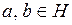 имеет место включение имеет место включение  . . Как правило, в каждой группе имеется много различных подгрупп. Например, всевозможные степени конкретного элемента группы образуют циклическую подгруппу. Отметим, что имеет место Теорема 4.2. Всякая подгруппа циклической группы является циклической. Во всякой некоммутативной группе  представляет интерес максимальная подгруппа элементов, коммутирующих со всеми элементами группы. Ее называют центром группы и обычно обозначают через представляет интерес максимальная подгруппа элементов, коммутирующих со всеми элементами группы. Ее называют центром группы и обычно обозначают через  а подгруппы а подгруппы  называют центральными подгруппами группы называют центральными подгруппами группы  Определение 4.2.Пусть  – собственная подгруппа группы – собственная подгруппа группы  Пусть Пусть  . Через . Через  обозначим множество элементов обозначим множество элементов  и назовем его левым смежным классом группы и назовем его левым смежным классом группы  по подгруппе по подгруппе  . . Если существует  , ,  , можно построить новый левый смежный класс , можно построить новый левый смежный класс  и так далее. и так далее. Аналогично строят правые смежные классы. Если каждый левый смежный класс совпадает с правым:  то тогда смежные классы называют двусторонними. Такими являются смежные классы в любой абелевой группе то тогда смежные классы называют двусторонними. Такими являются смежные классы в любой абелевой группе  Смежные классы обладают радом важных свойств. Смежные классы обладают радом важных свойств. Теорема 4.3. Пусть  – собственная подгруппа группы – собственная подгруппа группы  Тогда: Тогда: 1) каждый элемент  принадлежит какому-нибудь левому смежному классу по подгруппе принадлежит какому-нибудь левому смежному классу по подгруппе  ; ; 2) два элемента  принадлежат одному левому смежному классу тогда и только тогда, когда принадлежат одному левому смежному классу тогда и только тогда, когда  ; ; 3) любые два левых смежных класса либо не пересекаются, либо совпадают; 4) для всякого 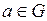 мощности множеств мощности множеств  и и  совпадают; совпадают; 5) G есть объединение попарно непересекающихся левых (правых) смежных классов по подгруппе  ; ; 6) Мощности множеств всех левых и соответственно правых смежных классов группы  по подгруппе по подгруппе  равны. равны. Определение 4.3. Индексом подгруппы  в группе в группе  называется мощность множества всех смежных классов группы называется мощность множества всех смежных классов группы  по данной подгруппе и обозначается через по данной подгруппе и обозначается через  . . С помощью свойств смежных доказывается важнейшая в теории конечных групп. Теорема 4.4 (теорема Лагранжа). Порядок конечной группы делится на порядок любой ее подгруппы. Следствие 1. В конечной группе индекс подгруппы равен частному от деления порядка группы на порядок подгруппы. Следствие 2. Любая группа простого порядка является циклической и не содержит собственных подгрупп. Следствие 3. Если  – конечная группа из n элементов, то для каждого – конечная группа из n элементов, то для каждого 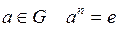 . Другими словами, в конечной группе порядок любого ее элемента делит порядок самой группы. . Другими словами, в конечной группе порядок любого ее элемента делит порядок самой группы. Определение 4.4.Подгруппа  группы группы  называется нормальной, если для каждого называется нормальной, если для каждого   . . Очевидно, всякая подгруппа индекса 2 является нормальной подгруппой. Задания для аудиторной работы Задание 4.1.Привести примеры подгрупп в группе  Образуют ли подгруппу: Образуют ли подгруппу: а) все отрицательные числа; все положительные числа; б) все четные числа; все нечетные числа; в) множество целых чисел от 0 до 10; от –5 до 5; д) все целые числа, делящиеся на 2009; е) все целые числа с остатком 1999 при делении на 2009? Задание 4.2.Привести примеры подгрупп а) в группе 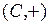 всех комплексных чисел с операцией сложения; б) в группе всех комплексных чисел с операцией сложения; б) в группе  Задание 4.3. Привести примеры подгрупп в группе  всех невырожденных вещественных квадратных всех невырожденных вещественных квадратных  матриц данного порядка матриц данного порядка  Найти центр этой группы. Найти центр этой группы. Задание 4.4.Много ли подгрупп у произвольной группы? Какова минимальная подгруппа, содержащая данный элемент группы? Какие еще элементы группы она должна содержать? Задание 4.5.Выяснить, является ли подгруппой: а) объединение подгрупп; б) дополнение к подгруппе; в) симметрическая разность двух подгрупп;
г) пересечение подгрупп; д) множество всех  -х степеней всех элементов абелевой группы. -х степеней всех элементов абелевой группы. Задание 4.6.В любой группе имеются циклические подгруппы (иногда совпадающие с самой группой). При каких условиях в группе имеются нециклические подгруппы? Привести примеры. Задание 4.7.Показать, что мультипликативная группа  абелева, но не циклична, а абелева, но не циклична, а  циклична. циклична. Задание 4.8.Пусть  – множество всевозможных строк-матриц с четырьмя координатами из – множество всевозможных строк-матриц с четырьмя координатами из 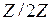 – группа относительно операции покоординатного сложения по модулю два. Сколько в этой группе элементов? – группа относительно операции покоординатного сложения по модулю два. Сколько в этой группе элементов? Пусть  – следующее подмножество элементов группы – следующее подмножество элементов группы   , ,
здесь 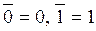 . Убедиться, что . Убедиться, что  подгруппа, выписать таблицу смежных классов группы подгруппа, выписать таблицу смежных классов группы  по по  Решение. Поскольку каждая из координат может независимо от других принимать лишь два значения, то мощность группы  равна 16. равна 16. Уже неоднократно обсуждалось, что операция покоординатного сложения по модулю два ассоциативна. Составив таблицу сложения элементов множества  , можно убедиться, что сложение этих элементов не выводит за пределы , можно убедиться, что сложение этих элементов не выводит за пределы  , то есть , то есть  замкнута относительно сложения. замкнута относительно сложения.  содержит нейтральный элемент – нулевой вектор. Каждый вектор из содержит нейтральный элемент – нулевой вектор. Каждый вектор из  обратен самому себе. Таким образом, обратен самому себе. Таким образом,  удовлетворяет всем аксиомам из определения группы. Следовательно, удовлетворяет всем аксиомам из определения группы. Следовательно,  – подгруппа группы – подгруппа группы  . . Выпишем таблицу всех смежных классов группы  по подгруппе по подгруппе  | № п/п | Класс  |  |  |  |  | |  | (0000) | (1011) | (0101) | (1110) | | (1000)  | (1000) | (0011) | (1101) | (0110) | | (0100)  | (0100) | (1111) | (1001) (0001) | (1010) | | (0010)  | (0010) | (1001) | (0111) | (1100) | Задание 4.9.Выписать все элементы мультипликативной группы  сравнить количество элементов этой группы с сравнить количество элементов этой группы с  Выяснить, является ли эта группа циклической. Выписать таблицу смежных классов Выяснить, является ли эта группа циклической. Выписать таблицу смежных классов  группы группы  по циклической подгруппе по циклической подгруппе  Решение.  . .  . .  Следовательно, Следовательно,  . Группа . Группа  циклична, если в ней найдется элемент порядка циклична, если в ней найдется элемент порядка  , то есть циклическая группа, порожденная некоторым элементом, совпадает со всей группой , то есть циклическая группа, порожденная некоторым элементом, совпадает со всей группой  Попытаемся найти такой элемент. Наудачу выпишем циклическую подгруппу Попытаемся найти такой элемент. Наудачу выпишем циклическую подгруппу 
 – подгруппа порядка 6. По теореме Лагранжа все остальные элементы этой подгруппы имеют порядки, являющиеся делителями 6. – подгруппа порядка 6. По теореме Лагранжа все остальные элементы этой подгруппы имеют порядки, являющиеся делителями 6.
 – –
подгруппа порядка 6. Следовательно, ее элементы 7, 19, 31, не принадлежащие 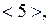 также имеют порядок, не превышающий 6. также имеют порядок, не превышающий 6.  – подгруппа порядка 6. Следовательно, ее элементы 11, 23, 35, не принадлежащие подгруппам – подгруппа порядка 6. Следовательно, ее элементы 11, 23, 35, не принадлежащие подгруппам 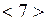 и и 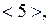 также имеют порядок, не превышающий 6. Таким образом, все 12 элементов группы также имеют порядок, не превышающий 6. Таким образом, все 12 элементов группы  имеют порядок, не превосходящий 6. Поэтому группа имеют порядок, не превосходящий 6. Поэтому группа  не может быть циклической. не может быть циклической.
 подгруппа из трех элементов. Поэтому таблица смежных классов подгруппа из трех элементов. Поэтому таблица смежных классов  должна состоять из должна состоять из  смежных классов. Одним из них всегда является подгруппа смежных классов. Одним из них всегда является подгруппа  Вот оставшиеся три смежных класса: Вот оставшиеся три смежных класса: 
 
Задание 4.10.Содержит ли группа 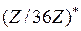 нециклическую подгруппу? нециклическую подгруппу? Решение. Да, содержит. В этой группе имеются три элемента второго порядка: 17, 19, 35. Эти элементы обратны сами себе, так как из условия  следует, что следует, что  Вместе с 1 они образуют замкнутую систему относительно умножения по модулю 36, и, следовательно, подгруппу – нециклическую подгруппу из четырех элементов. Вместе с 1 они образуют замкнутую систему относительно умножения по модулю 36, и, следовательно, подгруппу – нециклическую подгруппу из четырех элементов.
| 



 называется всякое непустое подмножество
называется всякое непустое подмножество  элементов множества
элементов множества  , которое в свою очередь является группой относительно той же операции. Подгруппа
, которое в свою очередь является группой относительно той же операции. Подгруппа  и
и 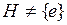 .
.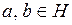 имеет место включение
имеет место включение  .
. а подгруппы
а подгруппы  называют центральными подгруппами группы
называют центральными подгруппами группы 
 Пусть
Пусть  . Через
. Через  обозначим множество элементов
обозначим множество элементов  и назовем его левым смежным классом группы
и назовем его левым смежным классом группы  ,
,  , можно построить новый левый смежный класс
, можно построить новый левый смежный класс  и так далее.
и так далее. то тогда смежные классы называют двусторонними. Такими являются смежные классы в любой абелевой группе
то тогда смежные классы называют двусторонними. Такими являются смежные классы в любой абелевой группе  Смежные классы обладают радом важных свойств.
Смежные классы обладают радом важных свойств. принадлежит какому-нибудь левому смежному классу по подгруппе
принадлежит какому-нибудь левому смежному классу по подгруппе  принадлежат одному левому смежному классу тогда и только тогда, когда
принадлежат одному левому смежному классу тогда и только тогда, когда  ;
;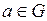 мощности множеств
мощности множеств  .
.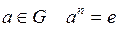 . Другими словами, в конечной группе порядок любого ее элемента делит порядок самой группы.
. Другими словами, в конечной группе порядок любого ее элемента делит порядок самой группы.
 .
. Образуют ли подгруппу:
Образуют ли подгруппу: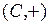 всех комплексных чисел с операцией сложения; б) в группе
всех комплексных чисел с операцией сложения; б) в группе 
 всех невырожденных вещественных квадратных
всех невырожденных вещественных квадратных  матриц данного порядка
матриц данного порядка  Найти центр этой группы.
Найти центр этой группы. -х степеней всех элементов абелевой группы.
-х степеней всех элементов абелевой группы. абелева, но не циклична, а
абелева, но не циклична, а  циклична.
циклична. – множество всевозможных строк-матриц с четырьмя координатами из
– множество всевозможных строк-матриц с четырьмя координатами из 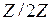 – группа относительно операции покоординатного сложения по модулю два. Сколько в этой группе элементов?
– группа относительно операции покоординатного сложения по модулю два. Сколько в этой группе элементов?
 ,
,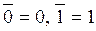 . Убедиться, что
. Убедиться, что  подгруппа, выписать таблицу смежных классов группы
подгруппа, выписать таблицу смежных классов группы 







 сравнить количество элементов этой группы с
сравнить количество элементов этой группы с  Выяснить, является ли эта группа циклической. Выписать таблицу смежных классов
Выяснить, является ли эта группа циклической. Выписать таблицу смежных классов  группы
группы  по циклической подгруппе
по циклической подгруппе 
 .
.  .
. Следовательно,
Следовательно,  . Группа
. Группа  , то есть циклическая группа, порожденная некоторым элементом, совпадает со всей группой
, то есть циклическая группа, порожденная некоторым элементом, совпадает со всей группой 
 – подгруппа порядка 6. По теореме Лагранжа все остальные элементы этой подгруппы имеют порядки, являющиеся делителями 6.
– подгруппа порядка 6. По теореме Лагранжа все остальные элементы этой подгруппы имеют порядки, являющиеся делителями 6. –
–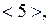 также имеют порядок, не превышающий 6.
также имеют порядок, не превышающий 6. – подгруппа порядка 6. Следовательно, ее элементы 11, 23, 35, не принадлежащие подгруппам
– подгруппа порядка 6. Следовательно, ее элементы 11, 23, 35, не принадлежащие подгруппам 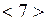 и
и  подгруппа из трех элементов. Поэтому таблица смежных классов
подгруппа из трех элементов. Поэтому таблица смежных классов  смежных классов. Одним из них всегда является подгруппа
смежных классов. Одним из них всегда является подгруппа 


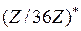 нециклическую подгруппу?
нециклическую подгруппу? следует, что
следует, что  Вместе с 1 они образуют замкнутую систему относительно умножения по модулю 36, и, следовательно, подгруппу – нециклическую подгруппу из четырех элементов.
Вместе с 1 они образуют замкнутую систему относительно умножения по модулю 36, и, следовательно, подгруппу – нециклическую подгруппу из четырех элементов.