 ПОЗНАВАТЕЛЬНОЕ
| Экспоненциальное сглаживание (адаптивная модель прогнозирования Брауна) 12
Метод средней скользящей простой 1.1 Сначала для временного ряда
1.2. Для первых
1.3. Затем интервал сглаживания сдвигается на один уровень вправо, повторяя вычисление средней арифметической. Для вычисления сглаженных уровней ряда
где
В результате такой процедуры получается Недостаток метода в том, что он применим лишь для линейных трендов.
Метод средней скользящей взвешенной
Отличие от предыдущего метода в том, что уровни, входящие в интервал сглаживания, суммируются с разными весами. Используется формула средней арифметической взвешенной
где
При краткосрочном прогнозировании наиболее эффективными оказываются адаптивные модели учитывающие неравномерность уровней временного ряда. Адаптивные модели прогнозирования – это модели дисконтирования данных, способные быстро приспосабливать свою структуру и параметры к изменению условий. Согласно схеме скользящего среднего, оценкой текущего уровня является взвешенное среднее всех предшествующих уровней, причем веса при наблюдениях убывают по мере удаления от последнего уровня, т.е. информационная ценность наблюдений признается тем большей, чем ближе они к концу интервала наблюдений.
Экспоненциальное сглаживание (адаптивная модель прогнозирования Брауна) Реакция на ошибку прогноза и дисконтирование уровней временного ряда в модели Брауна определяется с помощью параметров сглаживания (адаптации) - Высокое значение параметров
Рассмотрим этапы построения линейной адаптивной модели Брауна:
Прогноз можно получить, используя вспомогательную таблицу 1.1.
Таблица 1.1. Оценка параметров модели Брауна
Таблица 1.2. Оценка начальных значений параметров модели
где
Работа 2. Исследование транспортного рынка и моделирование товарной политики транспортного предприятия Для осуществления задач прогнозирования и стратегического планирования маркетинга фирмы широко используются различные матричные методы анализа такие как матрицы BCG и «Дженерал электрик» (GЄC) Бостонская консультативная группа и др. Матричные модели являются наглядными и удобными средствами выдачи стратегических рекомендаций по номенклатуре продукции или сегментам рынка в зависимости от их расположения в матрицах. Матрица дает возможность определить какие виды услуг занимают ведущее положение по их доле на рынке по сравнению с конкурентами, какова динамика их роста. Для железных дорог в соответствии с методикой построения матрицы БКГ выделяют большую, доходную, перспективную и ограниченную стратегические зоны освоения перевозок (СЗО). Основные СЗО характеризуются следующими особенностями: Большая СЗО – массовые перевозки топливно-сырьевых грузов. Спрос на эти перевозки стабильный, они занимают большую долю и имеют тенденцию к росту (зона залога успеха). Необходимо развивать, вкладывать капитальные затраты для развития инфраструктуры. Доходная СЗО –международные экспертно-импортные перевозки. Они занимают меньшую долю на рынке, но приносят большой доход и прибыль. Рост данных перевозок сомнителен, поэтому необходим контроль за капиталовложениями в эту сферу перевозок (развитие транспортных коридоров, гибких тарифов, взаимодействие видов транспорта). Перспективная СЗО– контейнерные перевозки. Железные дороги пока контролируют небольшую долю таких перевозок (~2%), однако спрос на них в будущем ожидается большой. Необходимо проведение активной инвестиционной политики, введение контрейлерных перевозок, активной рекламы. Ограниченная СЗО –короткопробежные перевозки прочих грузов. Данные перевозки бесперспективные и чаще всего невыгодные, поэтому от них следует по возможности избавляться, либо находить нетрадиционные методы освоения и расширения собственных автомобилей для доставки грузов от двери до двери, маршруты. По каждой из указанных четырех СЗО проводят подробные имитационные расчеты при разных вариантах освоения рынка, определяют необходимые потребности в инвестициях и других ресурсах в перспективе и рассчитывают экономическую эффективность принимаемой стратегии.
12 |



 определяется интервал сглаживания
определяется интервал сглаживания  . Необходимо при прочих равных условиях интервал сглаживания
. Необходимо при прочих равных условиях интервал сглаживания  брать нечетным;
брать нечетным; – большое число для сглаживания мелких беспорядочных колебаний;
– большое число для сглаживания мелких беспорядочных колебаний; применяется формула:
применяется формула: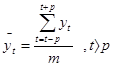
 (при нечетном
(при нечетном сглаженных значений уровней ряда, при этом первые
сглаженных значений уровней ряда, при этом первые  и последние
и последние 

 - вес
- вес  -го уровня временного ряда.
-го уровня временного ряда.
 , значения которых могут изменяться от 0 до 1.
, значения которых могут изменяться от 0 до 1.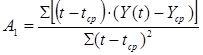


 - ошибка прогнозирования уровня
- ошибка прогнозирования уровня  , вычисленная в момент времени
, вычисленная в момент времени  на один шаг вперед.
на один шаг вперед.


