 ПОЗНАВАТЕЛЬНОЕ
| Границя функції двох змінних 12
Означення 12. Число B називається границею функції Зауваження. Для функції багатьох змінних справедливі теореми про границю суми, добутку та частки, які аналогічні відповідним теоремам для функції однієї незалежної змінної. Наведемо формулювання відповідних теорем. Теорема 1. Якщо функція Теорема 2. Якщо функція Теорема 3. Якщо Теорема 4. Нехай 1) 2) 3) Приклад. Обчислити Згідно з теоремами про арифметичні операції з границями, а також те, що границя сталої дорівнює сталій, тобто
Приклад. Обчислити Візьмемо Зауваження.Між поняттями границі в точці для функції однієї змінної та функції багатьох змінних є багато спільного, але є й принципова відмінність, яка робить поняття границі функції кількох змінних суттєво більш обмеженим, ніж поняття границі функції однієї змінної. Річ у тім, що коли Для функції двох змінних
Рис. 10 Рис. 11 Більше того, до точки можна наближатися не тільки по прямій, а й по більш складних траєкторіях (рис. 11). Очевидно, що рівність Приклад. Довести, що Будемо наближатися до точки (0; 0) по прямій Зауважимо, що значення границі залежить від кутового коефіцієнта прямої, наприклад: при при Таким чином, якщо наближатися до точки (0; 0) з різних напрямків, то дістанемо різні значення, тобто границя Зауваження. Нехай дано функцію двох змінних Якщо при будь-якому фіксованому y з Y існує для функції f(x; y) (яка буде функцією від х) границя при х → а, то ця границя, взагалі кажучи, буде залежати від наперед фіксованого у:
Далі постає запитання про границю функції
Повторні границі не обов’язково рівні. Приклад. Нехай 1)
але водночас Може статися так, що одна з повторних границь існує, друга - ні. Розглянемо приклади. 2) 3) В обох випадках існує повторна границя Приклади показують, що можливість перестановки границь повинна бути обґрунтована. У зв’язку з цим виконується наступна теорема, що встановлює зв’язок між подвійною і повторною границями. Теорема 5. Якщо 1) існує (скінченна або ні) подвійна границя
і 2) при будь-якому у з Y існує (скінченна) звичайна границя по х Доведемо це для випадку скінченних А, а і b. Згідно з означенням за заданим За умовою 2)
При фіксованому у з Y, що задовольняє умову Якщо поряд з умовами 1) і 2) при будь-якому х з Х існує (скінченна) звичайна границя по у З теореми 5 випливає, що в прикладах 1) і 2) подвійна границя не існує. У прикладі 3), навпаки, подвійна границя існує: 3 нерівності Не обов’язково існування подвійної границі необхідне для рівності повторних. У прикладі 12 |



 при
при  ,
,  , якщо для будь-якого
, якщо для будь-якого  існує число
існує число  таке, що при виконанні нерівності
таке, що при виконанні нерівності  виконується нерівність
виконується нерівність  і позначається
і позначається  або
або  .
. має границю при
має границю при  , то вона єдина.
, то вона єдина. має границю при
має границю при  .
. ,
,  і в деякому околі точки
і в деякому околі точки  , то
, то  .
. ,
,  . Тоді:
. Тоді: ;
; ;
; .
. .
. ,
,  , маємо
, маємо
 .
. .
. . Тоді з того, що
. Тоді з того, що  випливає
випливає 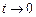 і задану границю можна переписати у вигляді
і задану границю можна переписати у вигляді  . При
. При  маємо
маємо  ;
;  , тобто
, тобто 
 . Таким чином,
. Таким чином,  .
. (
(  — функція однієї змінної), то це означає, що і лівостороння і правостороння границі дорівнюють b. Правильним є й обернене: з існування та збігу двох односторонніх границь випливає існування границі функції в точці.
— функція однієї змінної), то це означає, що і лівостороння і правостороння границі дорівнюють b. Правильним є й обернене: з існування та збігу двох односторонніх границь випливає існування границі функції в точці. наближатися до точки
наближатися до точки  можна нескінченною множиною способів: і справа, і зліва, і зверху, і знизу, і під кутом 30° до осі Ох тощо (рис. 10).
можна нескінченною множиною способів: і справа, і зліва, і зверху, і знизу, і під кутом 30° до осі Ох тощо (рис. 10).
 правильна тоді й тільки тоді, коли границя дорівнює b при наближенні до точки
правильна тоді й тільки тоді, коли границя дорівнює b при наближенні до точки  по будь-якій траєкторії. Це суттєво більш обмежене, ніж збіг двох односторонніх границь у випадку функції однієї змінної.
по будь-якій траєкторії. Це суттєво більш обмежене, ніж збіг двох односторонніх границь у випадку функції однієї змінної. не існує.
не існує. . Якщо
. Якщо  .
. границя дорівнює
границя дорівнює  .
. границя дорівнює
границя дорівнює  і т. п.
і т. п. не існує.
не існує.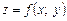 . Розглянемо границі, які дістаємо після послідовних граничних переходів за кожним із аргументів окремо в тому чи іншому порядку.
. Розглянемо границі, які дістаємо після послідовних граничних переходів за кожним із аргументів окремо в тому чи іншому порядку.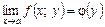 .
. при
при 
 — це буде одна із двох повторних границь. Іншу дістанемо, якщо границі візьмемо в зворотному порядку
— це буде одна із двох повторних границь. Іншу дістанемо, якщо границі візьмемо в зворотному порядку .
. і а = b = 0, тоді:
і а = b = 0, тоді: ,
, 
 ,
, ,
,  . Отже,
. Отже,  .
. або
або .
.
 , але немає повторної границі
, але немає повторної границі 
 (в останньому прикладі навіть не існує простої границі
(в останньому прикладі навіть не існує простої границі 
 , то існує повторна границя
, то існує повторна границя  , яка дорівнює подвійній границі.
, яка дорівнює подвійній границі. , що
, що  , якщо тільки
, якщо тільки  (причому х береться з Х, а у з Y). Зафіксуємо у так, щоб виконувалась нерівність
(причому х береться з Х, а у з Y). Зафіксуємо у так, щоб виконувалась нерівність  і перейдемо в
і перейдемо в  .
. .
. , що й треба було довести.
, що й треба було довести. , то, як випливає з доведеного, існує також і друга повторна границя
, то, як випливає з доведеного, існує також і друга повторна границя  , що дорівнює також числу А (в цьому випадку обидві повторні границі однакові).
, що дорівнює також числу А (в цьому випадку обидві повторні границі однакові). випливає, що вона дорівнює нулю.
випливає, що вона дорівнює нулю.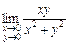 обидві повторні границі існують і рівні 0, але подвійної границі немає.
обидві повторні границі існують і рівні 0, але подвійної границі немає.