 ПОЗНАВАТЕЛЬНОЕ
| Множини точок на площині та в n-вимірному просторі 12
ЛЕКЦІЯ 9. Основні поняття функції багатьох змінних ПЛАН 1. Множини точок на площині та в n-вимірному просторі 2. Означення функції багатьох змінних 3. Способи задання функції 4. Знаходження області визначення функції двох змінних 5. Границя функції двох змінних
Множини точок на площині та в n-вимірному просторі Упорядкованій парі чисел Означення 1. Множина точок називається зв’язною, якщо будь-які її дві точки можна сполучити ламаною лінією так, щоб усі точки цієї лінії належали цій множині. Приклад. На рис. 1 буде зв’язна множина, а а на рис. 2 - не зв’язна.
Рис.1 Рис.2 Означення 2. Множина точок називається обмеженою, якщо всі її точки належать множині точок круга скінченного радіуса. Приклад. На рис. 3 маємо обмежену множину, на рис. 4 - необмежену.
Рис.3 Рис.4 Означення 3. Множина точок, координати яких задовольняють нерівність
називається d-околом точки Зауваження. У випадку двовимірного простору нерівність (1) можна подати у вигляді
Вона означає внутрішність круга з радіусом Якщо з d-околу точки Означення 4.Точка називається внутрішньою для множини точок, якщо вона належить цій множині разом з деяким своїм d-околом, і зовнішньою, якщо існує її окіл з точок, жодна з яких не належить цій множині. Означення 5. Зв’язна множина, яка складається тільки з внутрішніх точок, називається відкритою областю (або просто областю). Область позначатимемо:
(Читаємо: область D є множина точок площини з координатами (х; у), таких що У частинному випадку, коли D — прямокутник, область позначатимемо
Приклад. На рис. 4 множина точок D — область:
Означення 6. Точка називається межовою для області, якщо в будь-якому її d-околі існують точки, що не належать області і належать їй. Означення 7. Множина межових точок називається межею області. Означення 8. Область, об’єднана зі своєю межею, називається замкненою областю. Приклад. На рис.5 Означення 9. Множина називається опуклою, якщо будь-які точки множини можна зв’язати відрізком, який буде належати цій множині.
Рис. 4 Рис. 5 2. Означення функції багатьох змінних Означення 10. Якщо кожній точці Згідно з означенням функцію Зокрема, при n = 2 говорять, що задана функція двох змінних Наведемо приклади функції двох змінних. Приклад. Витратами на виробництво даного виробу при даній техніці виробництва є функція матеріальних витрат x і витрат на оплату робочої сили y: Це є функція витрат виробництва. Приклад. Розглянемо функцію двох незалежних змінних K, L, яка називається функцією виробництва, або функцією Кобба—Дугласа, де K — кількість капіталу, L — кількість праці, яку вкладено у виробництво Приклад. Припустимо, що предметами споживання будуть два товари А та В, ціни яких відповідно становлять p1 та p2. Якщо ціни інших товарів сталі, а прибуток споживачів та структура споживань не змінюються, то попит та пропозиція кожного з товарів залежить від їх цін. Маємо функцію попиту на товар А: Способи задання функції Як і функцію однієї змінної, функції двох змінних можна зобразити: — аналітично (у вигляді формули), наприклад:
— таблично (у вигляді таблиці), наприклад:
таблицею задана функція — графічно:
Для графічного зображення функції двох змінних використовуємо систему координат Оxyz у тривимірному просторі (рис. 6).
Рис. 6 Кожній парі чисел x та y відповідає точка Зауваження. На практиці побудувати графік функції важко, адже йдеться про зображення на площині просторової фігури, а це не завжди вдається. Приклад. Графічне зображення функції
Рис. 7 Рис. 8. Графічне зображення функції Існує й інший спосіб геометричного зображення функції двох змінних — зображення за допомогою ліній рівня. Означення 11. Лінією рівня називається множина всіх точок площини, в яких функція Рівняння ліній рівня записують у вигляді Накресливши кілька ліній рівня та зазначивши, яких значень набуває на них функція, дістанемо наближене уявлення про зміну функції. Елементарний приклад зображення функції за допомогою ліній рівня є зображення рельєфу місцевості на географічній карті. Висота місцевості над рівнем моря є функцією координат точки земної поверхні. За лініями рівня висоти, нанесеними на карту, легко уявити собі рельєф даної місцевості. 12 |



 на координатній площині відповідає одна точка
на координатній площині відповідає одна точка  . Аналогічно, в n-вимірному просторі n упорядкованим дійсним числам відповідає одна точка
. Аналогічно, в n-вимірному просторі n упорядкованим дійсним числам відповідає одна точка  , де числа
, де числа  будуть координатами
будуть координатами

 (1)
(1)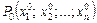 .
. (2)
(2) Рис.3
Рис.3 та з центром у точці
та з центром у точці  (рис. 3).
(рис. 3). вилучимо саму точку
вилучимо саму точку  .
.
 .
. .
. — замкнена область,
— замкнена область,  — рівняння межі області, К — внутрішня, L — зовнішня, М — межова точка.
— рівняння межі області, К — внутрішня, L — зовнішня, М — межова точка.

 множини D n-вимірного простору поставлено у відповідність за деяким законом одне і тільки одне дійсне число
множини D n-вимірного простору поставлено у відповідність за деяким законом одне і тільки одне дійсне число  , то кажуть, що в області
, то кажуть, що в області  задано функцію n незалежних змінних
задано функцію n незалежних змінних  . При цьому D називають областю визначення функції, Е — областю значень функції.
. При цьому D називають областю визначення функції, Е — областю значень функції. можна розглядати як функцію точки і записувати
можна розглядати як функцію точки і записувати  .
. , якщо кожній парі
, якщо кожній парі  на площині поставлено у відповідність тільки одне число z. Для прикладних питань економіки має значення розгляд функції двох або трьох незалежних змінних. Тому в подальшому більше уваги звертатимемо на ці
на площині поставлено у відповідність тільки одне число z. Для прикладних питань економіки має значення розгляд функції двох або трьох незалежних змінних. Тому в подальшому більше уваги звертатимемо на ці .
.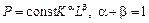 .
. ; функцію попиту на товар В:
; функцію попиту на товар В:  ; функцію пропозиції товару А:
; функцію пропозиції товару А: 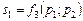 ; функцію пропозиції товару В:
; функцію пропозиції товару В:  .
. ,
, z
z ;
;
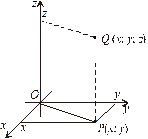
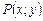 площини Оxy. У точці
площини Оxy. У точці  , яка позначається символом
, яка позначається символом 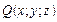 . Точки Q, які відповідають різним значенням незалежних змінних, утворюють певну поверхню у просторі. Така поверхня є графічним зображенням функції
. Точки Q, які відповідають різним значенням незалежних змінних, утворюють певну поверхню у просторі. Така поверхня є графічним зображенням функції  .
. є площина, яка проходить через точки (0; 0; 1), (0; 1; 0), (1; 0; 0) (рис. 7).
є площина, яка проходить через точки (0; 0; 1), (0; 1; 0), (1; 0; 0) (рис. 7).
 є півкуля (рис. 8).
є півкуля (рис. 8). .
.