ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Методика расчета горловины сортировочного парка

Вначале рассчитываются неизвестные углы поворота кривых на спускной части горки. Для каждого неизвестного угла нужно выбрать расчетный путь; на расчетном пути должен быть только один неизвестный угол.

Для определения неизвестного угла b расчетный путь представляется в виде ломаной линии, состоящей из отрезков li, i =1, … n (рис. 2.9); при этом кривые заменяют их тангенсами.

Рис. 2.9. Схема расчетного пути

Длину каждого отрезка ломаной можно определить как (см. рис. 2.10)

li = Ti + fi + Ti+1 (2.6)

где Ti , Ti+1 - тангенсы кривых, соответственно, в i-й и (i+1)-й вершинах;

fi - длина прямолинейного участка между i-й и (i+1)-й вершинами.

Длина тангенса определяется как

Ti= ;

при этом для вершин, являющихся центрами стрелочных переводов Ri= 0 и, следовательно, Ti=0.

Рис. 2.10. Определение длины отрезка ломаной линии

Неизвестный угол b можно найти из уравнения, в котором ордината расчетного пути Y определяется с использованием суммы проекций отрезков расчетного пути на ось OY

(*)

где y1 - ордината головного стрелочного перевода;

li - длина элемента;

qi - угол наклона элемента к оси абсцисс;

n - число элементов расчетного пути.

Угол наклона i-го элемента qi можно найти как алгебраическую сумму углов поворота во всех точках расчетного пути, начиная от головного стрелочного перевода

где j - угол наклона оси головного стрелочного перевода к оси абсцисс ;

aj - угол поворота расчетного пути в j-й точке.

Непосредственное решение приведенного уравнения для получения угла b затруднительно и поэтому был разработан итерационный метод, который не требует решения сложных тригонометрических уравнений и поэтому используется для автоматизации расчетов указанного угла. Сущность итерационного метода заключается в следующем.

Первоначально принимается некоторое начальное значение неизвестного угла b = b0 и при этом значении вычисляется ордината расчетного пути y(b0) c помощью выражения (*). Вычисленное значение у(b) сравнивается с ординатой расчетного пути Y. При этом в зависимости от результатов сравнения предыдущее значение угла b изменяется на заданную величину Db (шаг итерации):

bk+1 = bk + Db×sign(Y - y(bk)), k = 0, 1, 2,…

Указанная процедура повторяется до тех пор, пока не будет найден интервал [bk, bk+1], в котором величина Y - y(b) меняет знак. После этого поиск угла осуществляется внутри указанного интервала методом половинного деления (см. рис. 2.11.); расчеты завершаются при выполнении условия

ïY - y (bk )ï- e £ 0,

где e - требуемая точность определения ординаты расчетного пути.

Рис. 2.11. Определение угла b методом половинного деления

При найденном значении неизвестного угла b с помощью приведенных выражений определяются координаты xi, yi всех точек расчетного пути.

На остальных путях, маршрут на которые от вершины горки проходит через найденный угол b, определяются прямые вставки между крестовиной последней стрелки и вершиной угла поворота.

Обозначения величин, входящих в данное выражение, показаны на рис. 2.12

Рис. 2.12. Определение прямых вставок на путях пучка

В горочной горловине может быть несколько неизвестных углов, для каждого из которых должен быть задан отдельный расчетный путь; расчет указанных углов осуществляется поочередно.

В качестве расчетного можно выбрать любой путь горловины. Обычно выбирают один из крайних путей пучка (если пучок полный) или соседний с крайним (если пучок неполный). При этом целесообразно сделать несколько вариантов расчета при разных расчетных путях и выбрать лучший по условиям вписывания кривых на всех сортировочных путях.
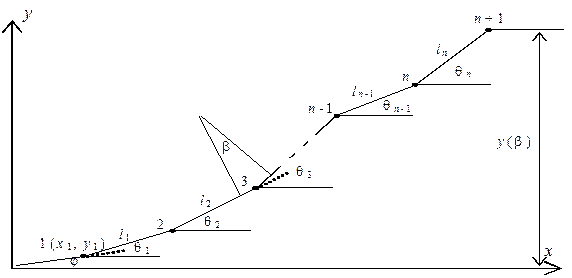