 ПОЗНАВАТЕЛЬНОЕ
| Методы выявления типа тенденции динамики
Прежде чем применить методы математического анализа для вычисления параметров уравнения тренда, необходимо выявить тип тенденции, а эта задача не является чисто математической. Наличие колебаний уровней крайне усложняет выявление типа тенденции и требует всестороннего подхода к этой проблеме, прежде всего качественного изучения характера развития объекта. При этом нужно дать ответ на такие вопросы: 1. Были ли условия развития объекта достаточно однородными в изучаемый период? 2. Каков характер действия основных факторов развития? 3. Не произошло ли качественное, существенное изменение условий развития объекта внутри изучаемого периода времени? Чем крупнее изучаемая система, чем больше факторов влияют на динамику изучаемого признака, тем реже возможны резкие, скачкообразные изменения в ряду динамики (не колебания, а именно изменения в тенденции). Большие и сложные системы обладают значительной инерцией, и для скачкообразного, резкого изменения тенденции такой системы требуются большие затраты ресурсов, которые общество выделить не в состоянии. Напротив, в масштабе отдельных предприятий вполне возможны резкие изменения, переходы от одной тенденции к другой. Рассмотрим некоторые основные типы уравнений тренда, выражающие те или иные качественные свойства развития. 1. Линейная форма тренда:
где а - начальный уровень тренда в момент или период, принятый за начало отсчета времени t; b - среднегодовой абсолютный прирост (среднее изменение за единицу времени); константа тренда.
Линейный тренд хорошо отражает тенденцию изменений при действии множества разнообразных факторов, изменяющихся различным образом по разным закономерностям. Равнодействующая этих факторов при взаимопогашении особенностей отдельных факторов (ускорение, замедление, нелинейность) часто выражается в примерно постоянной абсолютной скорости изменения, т.е. в прямолинейном тренде. Таковы, например, тенденции динамики урожайности для масштаба области, республики, крупного региона, страны в целом. 2. Параболическая форма тренда:
где с - квадратический параметр, равный половине ускорения; константа К параболического тренда.
Параболическая форма тренда выражает ускоренное или замедленное изменение уровней ряда с постоянным ускорением. Такой характер развития можно ожидать при наличии важных факторов прогрессивного развития (прогрессирующее поступление нового высокопроизводительного оборудования, увеличение среднесуточного прироста живого веса поросят с возрастом и т.п.). Ускоренное возрастание может происходить в период после снятия каких-то сдерживающих развитие преград - ограничений в распределении дохода, в уровне оплаты труда, при повышении цены реализации на дефицитную продукцию. Параболическая форма тренда с отрицательным ускорением (с < 0) приводит со временем не только к приостановке роста уровня, но к его снижению со все большей скоростью. Парабола 2-го порядка (квадратическая) имеет либо максимум (если с < 0 и b > 0), либо минимум (b < 0, с > 0). Для нахождения экстремума производную параболы по времени t следует приравнять нулю и решить полученное уравнение относительно t. 3. Экспоненциальная форма тренда:
где k - темп изменения в разах; константа тренда.
Если k > 1, экспоненциальный тренд выражает тенденцию ускоренного и все более ускоряющегося возрастания уровней. Такой характер свойствен, например, размножению организмов при отсутствии ограничения со стороны среды: кормов, пространства, хищников, болезней. При росте по экспоненте абсолютный прирост пропорционален достигнутому уровню. При k < 1 экспоненциальный тренд означает тенденцию постоянно все более замедляющегося снижения, уровней динамического ряда. Такая тенденция может быть присуща динамике трудоемкости продукции, удельных затрат топлива, металла на единицу полезного эффекта (на 1 кВт ч, на 1 м2 жилой площади и т.д.) при технологическом прогрессе; экстремальных точек экспонента не имеет. 4. Логарифмическая форма тренда:
Логарифмический тренд пригоден для отображения тенденции замедляющегося роста уровней при отсутствии предельного возможного значения. Замедление роста становится все меньше и меньше, и при достаточно большом t логарифмическая кривая становится малоотличимой от прямой линии. Логарифмический тренд пригоден для отображения роста спортивных достижений (чем они выше, тем труднее их улучшать), роста производительности агрегата по мере его освоения и совершенствования, повышения продуктивности скота или вообще эффективности системы при ее совершенствовании без качественных, коренных преобразований. Экстремума логарифмическая кривая не имеет. 5. Тренд в форме степенной кривой:
где b - константа тренда.
При b = 1 имеем линейный тренд, b = 2 - параболический и т.п. Степенная форма - гибкая, пригодная для отображения изменений с разной мерой пропорциональности изменений во времени. Жестким условием является обязательное прохождение через начало координат: при t = 0, 6. Гиперболическая форма тренда:
Если b > 0, гиперболический тренд выражает тенденцию замедляющегося снижения уровня, стремящегося к пределу a. Если b<0, тренд выражает тенденцию замедляющегося роста уровней, стремящихся в пределе к а. Следовательно, гиперболическая форма тренда подходит для отображения тенденции, процессов, ограниченных предельным значением уровня. 7. Логистическая форма тренда:
где е - основание натуральных логарифмов;
а, b - параметры тренда. Логистическая кривая имеет форму латинской буквы s положенной набок, отчего еще называется эс-образной кривой. Она имеет два перегиба: от ускоряющегося роста к равномерному (вогнутость) и от равномерного роста посреди периода к замедляющемуся (выпуклость). Она подходит для отображения развития в течение длительного периода, проходящего все фазы, например процесса насыщения потребителей каким-то новым товаром. После теоретического исследования особенностей разных форм тренда необходимо обратиться к фактическому ряду динамики, тем более что далеко не всегда можно надежно установить, какой должна быть форма тренда из чисто теоретических соображений. По фактическому динамическому ряду тип тренда устанавливают на основе графического изображения, путем осреднения показателей динамики, на основе статистической проверки гипотезы о постоянстве параметра тренда. Когда тип тренда установлен, необходимо вычислить оптимальные значения параметров тренда исходя из фактических уровней. Для этого обычно используют метод наименьших квадратов (МНК). Его суть уже рассмотрена в предыдущих главах, в данном случае оптимизация состоит в минимизации суммы квадратов отклонений фактических уровней ряда от выровненных уровней (от тренда). Для каждого типа тренда МНК дает систему нормальных уравнении, решая которую вычисляют параметры тренда. |



 (7.4.1)
(7.4.1)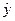 - уровни, освобожденные от колебаний, выровненные по прямой;
- уровни, освобожденные от колебаний, выровненные по прямой; (7.4.2)
(7.4.2) (7.4.3)
(7.4.3) (7.4.4)
(7.4.4) (7.4.5)
(7.4.5) = 0. Можно усложнить форму тренда:
= 0. Можно усложнить форму тренда:  или
или  , но эти уравнения нельзя логарифмировать, трудно вычислять параметры, и они крайне редко применяются.
, но эти уравнения нельзя логарифмировать, трудно вычислять параметры, и они крайне редко применяются. (7.4.6)
(7.4.6) (7.4.7)
(7.4.7) ,
, 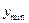 - максимальное и минимальное из возможных значений уровня;
- максимальное и минимальное из возможных значений уровня;