 ПОЗНАВАТЕЛЬНОЕ
| ПРИЛОЖЕНИЯ СТЕПЕННЫХ РЯДОВ
ЗАНЯТИЕ 13 РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ Ряды Тейлора и Маклорена Степенной ряд называют рядом Тейлора для функци Ряд
ДОСТАТОЧНЫЕ УСЛОВИЯ РАЗЛОЖИМОСТИ ФУНКЦИИ В РЯД ТЕЙЛОРА
Если
РАЗЛОЖЕНИЕ В РЯДЫ МАКЛОРЕНА НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Приведенные ниже разложения принято называть основными, так как на базе этих разложений можно, используя различные приемы, получать разложения в ряды Маклорена и Тейлора многих других функций. Основные разложения по степеням t имеют вид: · · · · · где · ·
Напомним, что
МЕТОДИКА РАЗЛОЖЕНИЕ ФУНКЦИИ 1) Построить степенной ряд для данной функции 2) Найти область сходимости полученного ряда, т.е. найти интервал сходимости и исследовать на сходимость ряд в концах этого интервала.
При разложении функции в ряд Тейлора или Маклорена, учитывая конкретное выражение, целесообразно сочетать разные приемы: 1)использование основных разложений по степеням 2)замену переменной; 3)арифметические операции: сложение, вычитание, умножение и деление степенных рядов; в первых трех случаях вновь полученный ряд сходится на пересечении областей сходимости рассматриваемых рядов. В случае деления вопрос решается изучением области сходимости полученного ряда; 4)поэлементное дифференцирование и интегрирование степенных рядов; при этом интервалы сходимости степенных рядов не меняются; 5)разложение правильной рациональной дроби в сумму простейших (элементарных) дробей.
Пример 1.Разложить функцию □ 1) Используя основное разложение для функции
2) Для отыскания области сходимости этого ряда учтём, что здесь Пример 2.Разложить функцию □ 1) С целью использования основного разложения сделаем тождественное преобразование: 2) Для отыскания области сходимости этого ряда учтём, что здесь
Пример 3.Разложить функцию □ 1) Найдём сначала разложение для функции 2) Для отыскания области сходимости учтем, что функцию Пример 4.Разложить функцию □ 1) Применяем тригонометрическую формулу
2) Для отыскания интервала сходимости используем признак Даламбера. Здесь
Вычислим:
при любом фиксированном Пример 5.Разложить функцию □ 1) С целью использования основного разложения для 2) Для отыскания области сходимости этого ряда учтём, что здесь
ПРИЛОЖЕНИЯ СТЕПЕННЫХ РЯДОВ
|



 , сходящийся на интервале
, сходящийся на интервале  ,
, в окрестности точки
в окрестности точки  , а также рядом по степеням
, а также рядом по степеням  .
. , сходящийся на интервале
, сходящийся на интервале  , называют рядом Маклорена для функци
, называют рядом Маклорена для функци  , а также рядом по степеням
, а также рядом по степеням  .
.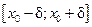 имеет производные любого порядка, ограниченные по модулю одним и тем же числом, т.е.
имеет производные любого порядка, ограниченные по модулю одним и тем же числом, т.е. 
 , то
, то 
 , где
, где  , или
, или  ;
; , где
, где  , где
, где  , где
, где  , или
, или  ;
;

 при
при  ;
;  ;
;  при
при  ;
;  ; полученный ряд принято называть биномиальным;
; полученный ряд принято называть биномиальным; , где
, где  ;
; , где
, где  ; при этом
; при этом  ; а
; а  – множество натуральных чисел.
– множество натуральных чисел. ;
; в ряд по степеням
в ряд по степеням  и указать область сходимости.
и указать область сходимости. и полагая
и полагая  , имеем:
, имеем: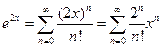 .
. – область сходимости степенного ряда. ■
– область сходимости степенного ряда. ■ и указать область сходимости.
и указать область сходимости.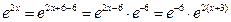 . Полагая теперь
. Полагая теперь  , используем основное разложение:
, используем основное разложение: 
 .
. , или
, или 
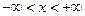 – область сходимости степенного ряда. ■
– область сходимости степенного ряда. ■ в ряд по степеням
в ряд по степеням  , где
, где  . Здесь использовано основное разложение для функции
. Здесь использовано основное разложение для функции 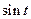 и замена переменной. Тогда
и замена переменной. Тогда  .
. , а второй ряд для
, а второй ряд для  сходится на
сходится на  . Тогда ряд для
. Тогда ряд для 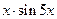 сходится на пересечении этих множеств, т.е. на
сходится на пересечении этих множеств, т.е. на 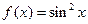 в ряд по степеням
в ряд по степеням  . Для разложения функции
. Для разложения функции  используем основное разложение для функции
используем основное разложение для функции  и замену переменной
и замену переменной 


 .
. , тогда
, тогда  .
.
 . Так как
. Так как  , то ряд сходится на промежутке
, то ряд сходится на промежутке  . В процессе упрощения использовано, что
. В процессе упрощения использовано, что  . ■
. ■ в ряд по степеням
в ряд по степеням  сделаем тождественное преобразование:
сделаем тождественное преобразование: 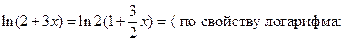
 а также замену переменной:
а также замену переменной: 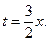 Тогда, используя основное разложение для функции
Тогда, используя основное разложение для функции 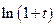 , имеем:
, имеем: 

 или
или  – область сходимости полученного степенного ряда. ■
– область сходимости полученного степенного ряда. ■