ИССЛЕДОВАНИЕ СТЕПЕННЫХ РЯДОВ
ЗАНЯТИЕ 12 Если ряд имеет вид  или или  (т.е. содержит все степени переменной), то можно воспользоваться формулой (т.е. содержит все степени переменной), то можно воспользоваться формулой  
или формулой  
В противном случае для отыскания  применяют признак Даламбера или Коши непосредственно к рядам применяют признак Даламбера или Коши непосредственно к рядам  или или  . . Для решения этой задачи следует: 1) записать ряд из абсолютных величин   2) найти интервал сходимости, применяя к ряду из абсолютных величин либо признак Даламбера, либо признак Коши, либо формулы (1), (2). При этом по признаку Даламбера вычисляют  , а по признаку Коши , а по признаку Коши  Полученный предел для сходимости ряда должен быть меньше единицы. Полученный предел для сходимости ряда должен быть меньше единицы. 3) исследовать граничные точки интервала. Пример 1.Найти радиус  и интервал сходимости степенного ряда и интервал сходимости степенного ряда  . . □ Заметим, что формулы  , ,  неприменимы, так как ряд содержит только нечетные степени неприменимы, так как ряд содержит только нечетные степени  . Обозначим . Обозначим  . Из вида коэффициентов . Из вида коэффициентов  следует, что нужно применить признак Даламбера. Для этого найдем следует, что нужно применить признак Даламбера. Для этого найдем 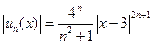 и и  . Вычислим . Вычислим   . Изучаемый ряд сходится, если полученный предел удовлетворяет условию: . Изучаемый ряд сходится, если полученный предел удовлетворяет условию:  , или , или 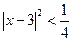 , или , или  . Итак, . Итак,  и интервал сходимости имеет вид и интервал сходимости имеет вид  , или , или  . . Пример 2.Найти область сходимости ряда 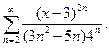 □ 1) Общий элемент ряда из абсолютных величин имеет вид: 
2) Применим признак Даламбера. Так как 
то вычислим 
 или или  интервал сходимости, интервал сходимости, 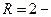 радиус сходимости. радиус сходимости.
3) Исследуем граничные точки. Подставляя  в исходный степенной ряд, получим числовой ряд в исходный степенной ряд, получим числовой ряд 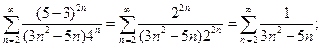 
Для исследования этого ряда на сходимость применим признак сравнения. Возьмем ряд с общим элементом  Этот ряд сходится. Вычислим Этот ряд сходится. Вычислим  изучаемый ряд сходится. изучаемый ряд сходится.
Подставляя  в исходный степенной ряд, получим числовой ряд в исходный степенной ряд, получим числовой ряд 
Этот ряд уже изучен: он сходится. Ответ:  − область сходимости ряда. ■ − область сходимости ряда. ■ Пример 3.Найти область сходимости ряда  □ 1) Общий элемент ряда из абсолютных величин имеет вид: 
2) Применим признак Даламбера. Вычислим 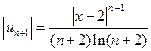 и и    тогда тогда  или или  интервал сходимости. интервал сходимости.
3) Исследуем граничные точки. Подставляя  в исходный степенной ряд, получим числовой ряд с общим элементом в исходный степенной ряд, получим числовой ряд с общим элементом  . .
Применим интегральный признак: 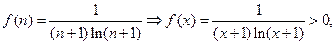 непрерывная, невозрастающая на непрерывная, невозрастающая на 
Вычислим 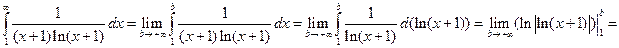
 интеграл расходится, следовательно, изучаемый ряд расходится. интеграл расходится, следовательно, изучаемый ряд расходится.
Подставим  Общий элемент ряда Общий элемент ряда  имеет вид: имеет вид:  ряд с таким общим элементом − знакочередующийся; сначала изучим его на абсолютную сходимость. ряд с таким общим элементом − знакочередующийся; сначала изучим его на абсолютную сходимость.
 ряд с таким общим элементом изучен, он расходится. Тогда исходный ряд изучим на условную сходимость: так как ряд ряд с таким общим элементом изучен, он расходится. Тогда исходный ряд изучим на условную сходимость: так как ряд  знакочередующийся и справедливо знакочередующийся и справедливо  при при  то сравним то сравним  и и  . .
Здесь 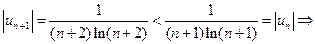 по признаку Лейбница ряд условно сходится. по признаку Лейбница ряд условно сходится. Ответ:  область сходимости ряда. ■ область сходимости ряда. ■ Пример 4.Найти область сходимости ряда  □ 1) Общий элемент ряда из абсолютных величин имеет вид 
2) Применим признак Коши, так как все выражение в степени, зависящей от n. 
 интервал сходимости. интервал сходимости.
3) Изучим граничные точки. Подставляя  в исходный степенной ряд, получим числовой ряд с общим элементом в исходный степенной ряд, получим числовой ряд с общим элементом  ряд с таким общим элементом – знакочередующийся. ряд с таким общим элементом – знакочередующийся.
Изучим его на абсолютную сходимость: 
 т.е. признак Коши не дает ответа на вопрос о сходимости. т.е. признак Коши не дает ответа на вопрос о сходимости.
Тогда вычислим 
 ряд расходится, так как для сходящегося ряда ряд расходится, так как для сходящегося ряда 
Подставляя  в исходный степенной ряд, получим числовой ряд с общим элементом в исходный степенной ряд, получим числовой ряд с общим элементом 
 общий элемент знакоотрицательного ряда, который получен из ряда с общим элементом общий элемент знакоотрицательного ряда, который получен из ряда с общим элементом 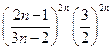 , рассмотренным в правой граничной точке, умножением на , рассмотренным в правой граничной точке, умножением на  Известно, что умножение ряда на число, не равное 0, не меняет его поведения в смысле сходимости. Поэтому изучаемый ряд расходится. Известно, что умножение ряда на число, не равное 0, не меняет его поведения в смысле сходимости. Поэтому изучаемый ряд расходится.
Ответ:  область сходимости ряда. ■ область сходимости ряда. ■
| 



 или
или  (т.е. содержит все степени переменной), то можно воспользоваться формулой
(т.е. содержит все степени переменной), то можно воспользоваться формулой



 применяют признак Даламбера или Коши непосредственно к рядам
применяют признак Даламбера или Коши непосредственно к рядам  или
или  .
.

 , а по признаку Коши
, а по признаку Коши  Полученный предел для сходимости ряда должен быть меньше единицы.
Полученный предел для сходимости ряда должен быть меньше единицы. .
. . Обозначим
. Обозначим  . Из вида коэффициентов
. Из вида коэффициентов  следует, что нужно применить признак Даламбера. Для этого найдем
следует, что нужно применить признак Даламбера. Для этого найдем 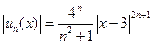 и
и  . Вычислим
. Вычислим 
 . Изучаемый ряд сходится, если полученный предел удовлетворяет условию:
. Изучаемый ряд сходится, если полученный предел удовлетворяет условию:  , или
, или 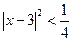 , или
, или  . Итак,
. Итак,  и интервал сходимости имеет вид
и интервал сходимости имеет вид  , или
, или  .
.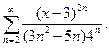



 или
или  интервал сходимости,
интервал сходимости, 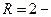 радиус сходимости.
радиус сходимости. в исходный степенной ряд, получим числовой ряд
в исходный степенной ряд, получим числовой ряд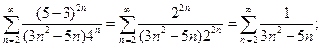

 Этот ряд сходится. Вычислим
Этот ряд сходится. Вычислим изучаемый ряд сходится.
изучаемый ряд сходится. в исходный степенной ряд, получим числовой ряд
в исходный степенной ряд, получим числовой ряд
 − область сходимости ряда. ■
− область сходимости ряда. ■

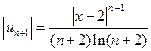 и
и 

 тогда
тогда  или
или  интервал сходимости.
интервал сходимости. в исходный степенной ряд, получим числовой ряд с общим элементом
в исходный степенной ряд, получим числовой ряд с общим элементом .
.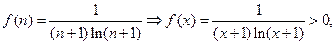 непрерывная, невозрастающая на
непрерывная, невозрастающая на 
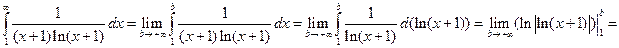
 интеграл расходится, следовательно, изучаемый ряд расходится.
интеграл расходится, следовательно, изучаемый ряд расходится. Общий элемент ряда
Общий элемент ряда  имеет вид:
имеет вид: ряд с таким общим элементом − знакочередующийся; сначала изучим его на абсолютную сходимость.
ряд с таким общим элементом − знакочередующийся; сначала изучим его на абсолютную сходимость. ряд с таким общим элементом изучен, он расходится. Тогда исходный ряд изучим на условную сходимость: так как ряд
ряд с таким общим элементом изучен, он расходится. Тогда исходный ряд изучим на условную сходимость: так как ряд  знакочередующийся и справедливо
знакочередующийся и справедливо  при
при  то сравним
то сравним  и
и  .
.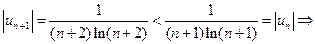 по признаку Лейбница ряд условно сходится.
по признаку Лейбница ряд условно сходится. область сходимости ряда. ■
область сходимости ряда. ■


 интервал сходимости.
интервал сходимости. в исходный степенной ряд, получим числовой ряд с общим элементом
в исходный степенной ряд, получим числовой ряд с общим элементом ряд с таким общим элементом – знакочередующийся.
ряд с таким общим элементом – знакочередующийся.
 т.е. признак Коши не дает ответа на вопрос о сходимости.
т.е. признак Коши не дает ответа на вопрос о сходимости.
 ряд расходится, так как для сходящегося ряда
ряд расходится, так как для сходящегося ряда 
 в исходный степенной ряд, получим числовой ряд с общим элементом
в исходный степенной ряд, получим числовой ряд с общим элементом
 общий элемент знакоотрицательного ряда, который получен из ряда с общим элементом
общий элемент знакоотрицательного ряда, который получен из ряда с общим элементом 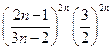 , рассмотренным в правой граничной точке, умножением на
, рассмотренным в правой граничной точке, умножением на  Известно, что умножение ряда на число, не равное 0, не меняет его поведения в смысле сходимости. Поэтому изучаемый ряд расходится.
Известно, что умножение ряда на число, не равное 0, не меняет его поведения в смысле сходимости. Поэтому изучаемый ряд расходится. область сходимости ряда. ■
область сходимости ряда. ■