 ПОЗНАВАТЕЛЬНОЕ
| Дифференциальные уравнения 1-го порядка
1.1. Обыкновенные дифференциальные уравнения. Определение 1. Обыкновенным дифференциальным уравнением n-го порядка для функции y аргумента x называется соотношение вида
где F – заданная функция своих аргументов. В названии этого класса математических уравнений термин «дифференциальные» подчеркивает, что в них входят производные Обыкновенное дифференциальное уравнение может не содержать в явном виде аргумент x, искомую функцию а) б) При написании обыкновенных дифференциальных уравнений часто используются обозначения производных через дифференциалы: в) г) Определение 2. Функция
имеет решение Найти тем или иным приёмом, например, подбором, одну функцию, удовлетворяющую уравнению, не означает решить его. Решить обыкновенное дифференциальное уравнение – значит найти все функции, образующие при подстановке в уравнение тождество. Для уравнения (1.1) семейство таких функций образуется с помощью произвольных постоянных и называется общим решением обыкновенного дифференциального уравнения n-го порядка, причём число констант совпадаёт с порядком уравнения:
причём второе слагаемое может быть записано и как Придавая некоторые допустимые значения всем произвольным постоянным в общем решении или в общем интеграле, получаем определённую функцию, уже не содержащую произвольных констант. Эта функция называется частным решением или частным интегралом уравнения (1.1). Для отыскания значений произвольных констант, а следовательно, и частного решения, используются различные дополнительные условия к уравнению (1.1). Например, могут быть заданы так называемые начальные условия при
В правых частях начальных условий (1.2) заданы числовые значения функции и производных, причём общее число начальных условий равно числу определяемых произвольных констант. Задача отыскания частного решения уравнения (1.1) по начальным условиям называется задачей Коши. 1.2. Обыкновенные дифференциальные уравнения 1-го порядка Обыкновенное дифференциальное уравнение 1-го порядка ( Теорема. Если в уравнении Геометрически общее решение уравнения 1-го порядка представляет собой семейство кривых на плоскости XOY, не имеющих общих точек и отличающихся друг от друга одним параметром – значением константы C. Эти кривые называются интегральными кривыми для данного уравнения. Интегральные кривые уравнения Замечание: Необходимо отметить, что к уравнению 1.3. Дифференциальные уравнения 1-го порядка Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
или уравнение вида
Чтобы в уравнении (3.1) разделить переменные, т.е. привести это уравнение к так называемому уравнению с разделёнными переменными, необходимо множители, содержащие переменную x перенести в одну сторону уравнения, а множители, содержащие переменную y, – в другую, а именно:
Остается проверить, не потеряны ли решения при делении на выражения, зависящие от переменных. Для этого необходимо решить уравнение Уравнение (3.2) приводится к уравнению с разделёнными переменными делением на произведение
что позволяет получить общий интеграл уравнения (3.2):
Функции (3.3), определяющие интегральные кривые, будут дополнены решениями Пример. Решить уравнение: Решение. Разделяем переменные:
Интегрируя, получаем
Из уравнений 1.4. Однородные дифференциальные уравнения 1-го порядка Определение 1. Уравнение 1-го порядка Пример 1. Показать, что функция Решение.
что и требовалось доказать. Теорема. Любая функция Доказательство.Первое утверждение теоремы очевидно, так как ОПРЕДЕЛЕНИЕ 2. Уравнение
где M и N – однородные функции одной и той же степени, т.е. обладают свойством Очевидно, что уравнение (4.1) всегда может быть приведено к виду
хотя для его решения можно этого и не делать. Однородное уравнение (4.1) приводится к уравнению с разделяющимися переменными с помощью замены искомой функции y по формуле
Или Интегрируя последнее равенство, получаем общий интеграл уравнения (4.3) относительно функции
и становится уравнением с разделяющимися переменными. Его решениями являются функции, определяющие на плоскости полупрямые:
Замечание. Иногда целесообразно вместо указанной выше замены использовать замену 1.5. Дифференциальные уравнения,приводящиеся к однородным Рассмотрим уравнение вида
Если
приводится к однородному уравнению Если
Сделав замену ПРИМЕР 1.Проинтегрировать уравнение
и выделить интегральную кривую, проходящую через точки: а) (2; 2); б) РЕШЕНИЕ.Положим Сокращая на
Разделим переменные: Интегрируя, получим: Заменяя z на
или, что то же самое,
Равенство (5.2) определяет семейство окружностей
Центры указанных окружностей лежат на прямой Определим, какие из найденных окружностей, удовлетворяют начальным условиям, т.е. решим задачи Коши: а) полагая в общем интеграле б) ни одна из окружностей (5.2) не проходит через точку ПРИМЕР 2. Решить уравнение: Решение.Исходное уравнение является частным случаем уравнения (5.1). Определитель Выполняя в заданном уравнении замену
Интегрируя последнее уравнение после подстановки 1.6. Обобщенное однородное уравнение Определение. Уравнение Например, таковым будет уравнение
Действительно, при сделанном предположении относительно измерений x, y,dx и dy члены левой части
Это условие выполняется при Обобщенное однородное уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки
Решая полученное уравнение путем разделения переменных, находим 1.7. Линейные дифференциальные уравнения 1-го порядка Определение. Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и её производной. Оно имеет вид:
где
и называется линейным однородным уравнением, в противном случае ( Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными:
Выражение (7.3) определяет общее решение уравнения (7.2). Чтобы найти общее решение уравнения (7.1), в котором функция
Подставляя найденную производную в уравнение (7.1), получим:
или
Отсюда
где В результате общее решение неоднородного линейного уравнения (7.1) будет иметь вид:
Заметим, что первое слагаемое в выражении (7.4) представляет общее решение (7.3) линейного однородного дифференциального уравнения (7.2), а второе слагаемое – частное решение линейного неоднородного уравнения (7.1), полученное из общего (7.4) при Теорема. Если известно одно частное решение линейного неоднородного дифференциального уравнения Однако надо отметить, что для решения линейного неоднородного дифференциального уравнения 1-го порядка (7.1) чаще применяется другой метод, иногда называемый методом Бернулли. Будем искать решение уравнения (7.1) в виде
Подставим найденную производную в исходное уравнение (7.1), получим:
Объединим, например, второе и третье слагаемые последнего выражения и вынесем функцию u(x) как общий множитель за скобку:
Потребуем обращения в нуль круглой скобки:
Решим уравнение (7.6), полагая произвольную постоянную C равной нулю:
Найденную функцию v(x) подставим в уравнение (7.5), откуда получим:
Решая его, приходим к: Следовательно, общее решение линейного дифференциального уравнения 1-го порядка (7.1) имеет вид: 1.8. Уравнение Бернулли Определение.Дифференциальное уравнение вида
где Предполагая, что
Введём новую функцию
Умножим обе части уравнения (8.1) на
т.е. для функции z(x) получили линейное неоднородное уравнение 1-го порядка. Это уравнение решается методами, разобранными в предыдущем разделе 1.7. Подставим в его общее решение вместо z(x) выражение ПРИМЕР. Найти общее решение уравнения:
Решение.Уравнение (8.2) является уравнением Бернулли, причём Будем искать решение уравнения в виде
В левой части последнего уравнения сгруппируем второе и третье слагаемые, которые содержат функцию u(x), и потребуем, чтобы
Следовательно, общее решение уравнения (8.2) имеет вид:
1.9. Дифференциальные уравнения в полных дифференциалах Определение. Если в уравнении
левая часть есть полный дифференциал некоторой функции Например, уравнение Теорема. Предположим, что функции M и N определены и непрерывны в некоторой односвязной области D и имеют в ней непрерывные частные производные соответственно по y и по x. Тогда, для того чтобы уравнение (9.1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество
Доказательство.Доказательство необходимости этого условия очевидно. Поэтому докажем достаточность условия (9.2). Покажем, что может быть найдена такая функция Действительно, поскольку
где Продифференцируем равенство (9.3) по y:
Но
Положим Итак, построена функция для которой ПРИМЕР. Найти общий интеграл уравнения:
Решение.В данном случае
Тогда
Следовательно, заданное дифференциальное уравнение 1-го порядка является уравнением в полных дифференциалах, т.е. существует такая функция
Проинтегрируем первое из двух соотношений по x:
Теперь продифференцируем
Отсюда 1.10. Интегрирующий множитель Определение. Если уравнение
становится уравнением в полных дифференциалах, т.е. В случае, когда уравнение является уравнением в полных дифференциалах, полагают Если найден интегрирующий множитель µ, то интегрирование данного уравнения сводится к умножению обеих его частей на µ и нахождению общего интеграла полученного уравнения в полных дифференциалах. Если µесть непрерывно дифференцируемая функция от x и y, то имеем тождество:
Из этого тождества следует, что интегрирующий множитель µ удовлетворяет уравнению с частными производными 1-го порядка:
Если заранее известно, что
где
т.е. указанная дробь является функцией только переменной ω. Решая уравнение (10.2), находим интегрирующий множитель
В частности, уравнение или 2. Дифференциальные уравнения 2-го порядка 2.1. Методы понижения порядка уравнения Дифференциальное уравнение 2-го порядка имеет вид:
Общим решением уравнения (1.1) является семейство функций, зависящее от двух произвольных постоянных Получить общее решение или решить задачу Коши для дифференциального уравнения 2-го порядка аналитически удаётся далеко не всегда. Однако в некоторых случаях удаётся понизить порядок уравнения с помощью введения различных подстановок. Разберем эти случаи. 1. Уравнения, не содержащие явно независимой переменной
т.е. в уравнении (1.1) явно не присутствует независимая переменная
Таким образом, уравнение 2-го порядка Пример 1. Решить дифференциальное уравнение Решение. Так как в исходном уравнении в явном виде отсутствует аргумент
Последнее уравнение является дифференциальным уравнением с разделяющимися переменными, а значит Так как при начальном условии 2. Уравнения, не содержащие явно искомой функции Решая последнее уравнение, получаем общий интеграл заданного дифференциального уравнения
Пример 2. Найти общее решение уравнения: Решение. В данное уравнение 2-го порядка явно не входит искомая функция
или
Полученное уравнение является линейным уравнением. Решая его, получаем:
или
Итак, для функции
откуда следует общее решение исходного уравнения:
3. Порядок степени понижается, если удаётся преобразовать его к такому виду, что обе части уравнения становятся полными производными по x от каких-нибудь функций. Например, рассмотрим уравнение
Следовательно, порядок уравнения понижен. 2.2. Линейное дифференциальное уравнение 2-го порядка Определение. Линейное дифференциальное уравнение (ЛДУ) 2-го порядка имеет следующий вид:
где Предполагая, что
Примем без доказательства, что уравнение (2.2) имеет на некотором промежутке единственное решение, удовлетворяющее любым начальным условиям Если Рассмотрим свойства решений ЛОДУ 2-го порядка. Определение. Линейной комбинацией функций Теорема. Если
то их линейная комбинация Доказательство.Поставим выражение
Перегруппируем слагаемые:
Поскольку функции Следствие 1. Из доказанной теоремы вытекает при Следствие 2. Полагая в теореме Замечание. Доказанное в теореме свойство решений остается справедливым для ЛОДУ любого порядка. 2.3. Определитель Вронского Определение. Система функций В случае двух функций Пусть
Действительно,
Поскольку функции
т.е.
Отсюда
В правой части последнего равенства необходимо оставить знак плюс, так как только в этом случае при
Полученная формула называется формулой Лиувилля. Выше было показано, что определитель Вронского для линейно независимых функций не может быть тождественно равен нулю. Следовательно, существует такая точка 2.4. Структура общего решения ЛОДУ 2-го порядка Теорема. Если |
 , (1.1)
, (1.1) (функции, образованные как результат дифференцирования); термин «обыкновенные» говорит о том, что искомая функция зависит только от одного действительного аргумента.
(функции, образованные как результат дифференцирования); термин «обыкновенные» говорит о том, что искомая функция зависит только от одного действительного аргумента. и любые её производные, но старшая производная
и любые её производные, но старшая производная  обязана входить в уравнение n-го порядка. Например,
обязана входить в уравнение n-го порядка. Например, – уравнение первого порядка;
– уравнение первого порядка; – уравнение третьего порядка.
– уравнение третьего порядка. – уравнение второго порядка;
– уравнение второго порядка; – уравнение первого порядка, образующее после деления на dx эквивалентную форму задания уравнения:
– уравнение первого порядка, образующее после деления на dx эквивалентную форму задания уравнения:  .
. называется решением обыкновенного дифференциального уравнения, если при подстановке в него
называется решением обыкновенного дифференциального уравнения, если при подстановке в него  оно обращается в тождество. Например, уравнение 3-го порядка
оно обращается в тождество. Например, уравнение 3-го порядка
 .
. Общее решение может быть явно не разрешено относительно y(x):
Общее решение может быть явно не разрешено относительно y(x):  В этом случае решение принято называть общим интегралом уравнения (1.1). Например, общим решением дифференциального уравнения
В этом случае решение принято называть общим интегралом уравнения (1.1). Например, общим решением дифференциального уравнения  является следующее выражение:
является следующее выражение: ,
,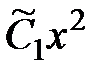 , так как произвольная постоянная
, так как произвольная постоянная  , может быть заменена новой произвольной постоянной
, может быть заменена новой произвольной постоянной  .
. :
: . (1.2)
. (1.2) ) имеет вид:
) имеет вид:  или (если его удаётся разрешить относительно производной)
или (если его удаётся разрешить относительно производной)  . Общее решение
. Общее решение  или общий интеграл
или общий интеграл  уравнения 1-го порядка содержат одну произвольную постоянную. Единственное начальное условие для уравнения 1-го порядка
уравнения 1-го порядка содержат одну произвольную постоянную. Единственное начальное условие для уравнения 1-го порядка  позволяет определить значение константы из общего решения или из общего интеграла. Таким образом можно найти частное решение, т.е. задача Коши будет решена. Вопрос о существовании и единственности решения задачи Коши является одним из центральных в общей теории обыкновенных дифференциальных уравнений. Для уравнения 1-го порядка, в частности, справедлива следующая теорема, принимаемая здесь без доказательства.
позволяет определить значение константы из общего решения или из общего интеграла. Таким образом можно найти частное решение, т.е. задача Коши будет решена. Вопрос о существовании и единственности решения задачи Коши является одним из центральных в общей теории обыкновенных дифференциальных уравнений. Для уравнения 1-го порядка, в частности, справедлива следующая теорема, принимаемая здесь без доказательства.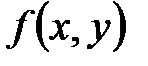 и её частная производная
и её частная производная  непрерывны в некоторой области D плоскости XOY и в этой области задана точка
непрерывны в некоторой области D плоскости XOY и в этой области задана точка  , то существует (и притом единственное) решение
, то существует (и притом единственное) решение  , удовлетворяющее как уравнению
, удовлетворяющее как уравнению  , так и начальному условию
, так и начальному условию  .
. обладают очевидным геометрическим свойством: в каждой точке
обладают очевидным геометрическим свойством: в каждой точке  тангенс угла наклона касательной к кривой равен значению правой части уравнения в этой точке:
тангенс угла наклона касательной к кривой равен значению правой части уравнения в этой точке:  . Другими словами, уравнение
. Другими словами, уравнение  приводится уравнение
приводится уравнение  и так называемое уравнение в симметрической форме
и так называемое уравнение в симметрической форме  .
. (3.1)
(3.1) . (3.2)
. (3.2)


 .
. . Если оно имеет вещественное решение
. Если оно имеет вещественное решение  , то
, то 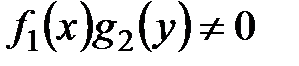 :
: ,
, . (3.3)
. (3.3) , если такие решения существуют.
, если такие решения существуют. .
.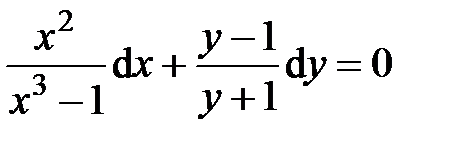 ;
;  .
. .
. и
и  находим
находим  ,
,  ,
,  . Непосредственной подстановкой этих функций в исходное уравнение убеждаемся, что эти решения – частные решения.
. Непосредственной подстановкой этих функций в исходное уравнение убеждаемся, что эти решения – частные решения. справедливо соотношение
справедливо соотношение  , называемое условием однородности функции двух переменных нулевого измерения.
, называемое условием однородности функции двух переменных нулевого измерения. – однородная нулевого измерения.
– однородная нулевого измерения.
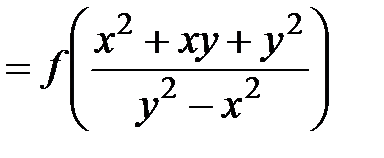 ,
,  ,
,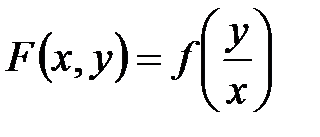 – однородна и, наоборот, любая однородная функция
– однородна и, наоборот, любая однородная функция  нулевого измерения приводится к виду
нулевого измерения приводится к виду  .
. . Докажем второе утверждение. Положим
. Докажем второе утверждение. Положим  , тогда для однородной функции
, тогда для однородной функции  ,что и требовалось доказать.
,что и требовалось доказать. , (4.1)
, (4.1) при всех
при всех  , называется однородным.
, называется однородным. , (4.2)
, (4.2) , где
, где 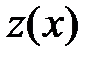 – новая искомая функция. Выполнив эту замену в уравнении (4.2), получим:
– новая искомая функция. Выполнив эту замену в уравнении (4.2), получим: (4.3)
(4.3) , т.е.
, т.е.  .
.
 , который после повторной замены
, который после повторной замены  даёт общий интеграл исходного уравнения (4.2). Кроме того, если
даёт общий интеграл исходного уравнения (4.2). Кроме того, если  – корни уравнения
– корни уравнения  , то функции
, то функции  (где
(где  ) – решения однородного уравнения (4.2). Если же
) – решения однородного уравнения (4.2). Если же  , то уравнение (4.2) принимает вид
, то уравнение (4.2) принимает вид
 .
. .
. . (5.1)
. (5.1) , то уравнение (5.1) с помощью замены
, то уравнение (5.1) с помощью замены  , где
, где  и
и 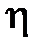 – новые переменные, а
– новые переменные, а  и
и  – некоторые постоянные числа, определяемые из системы
– некоторые постоянные числа, определяемые из системы ,
, .
. , то уравнение (5.1) принимает вид:
, то уравнение (5.1) принимает вид: .
. , получим уравнение, не содержащее независимую переменную.
, получим уравнение, не содержащее независимую переменную.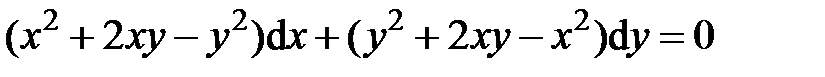
 .
. и
и  .
.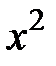 и собирая члены при dx иdz, получим:
и собирая члены при dx иdz, получим: .
.
 .
. ; или
; или  , где
, где  .
. , получим общий интеграл исходного уравнения в виде
, получим общий интеграл исходного уравнения в виде

 . (5.2)
. (5.2) .
. и в начале координат касаются прямой
и в начале координат касаются прямой  . Функция
. Функция  , в свою очередь, является частным решением заданного дифференциального уравнения.
, в свою очередь, является частным решением заданного дифференциального уравнения. ,
,  , находим
, находим 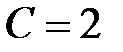 ,поэтому искомой кривой является окружность
,поэтому искомой кривой является окружность  ;
; проходит через эту точку, а значит, соответствующая функция
проходит через эту точку, а значит, соответствующая функция  .
. в данном случае не равен нулю, поэтому сначала рассмотрим систему
в данном случае не равен нулю, поэтому сначала рассмотрим систему  .Решая указанную систему, получим, что
.Решая указанную систему, получим, что 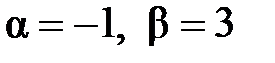 .
. , приходим к однородному уравнению
, приходим к однородному уравнению .
. , находим
, находим 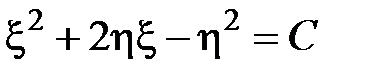 . Возвращаясь к старым переменным x и y по формулам
. Возвращаясь к старым переменным x и y по формулам  , имеем
, имеем  .
. )-го измерения.
)-го измерения. . (6.1)
. (6.1)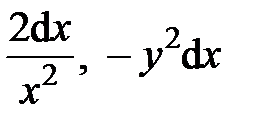 и dy будут иметь соответственно измерения (–2), (2k) и(k–1). Приравнивая эти величины, получаем условие, которому должно удовлетворять искомое число k:
и dy будут иметь соответственно измерения (–2), (2k) и(k–1). Приравнивая эти величины, получаем условие, которому должно удовлетворять искомое число k: .
. (при таком k все члены левой части рассматриваемого уравнения будут иметь измерение (–2)). Следовательно, уравнение (6.1) является обобщённым однородным.
(при таком k все члены левой части рассматриваемого уравнения будут иметь измерение (–2)). Следовательно, уравнение (6.1) является обобщённым однородным. , где z – новая неизвестная функция. Проинтегрируем уравнение (6.1) описанным методом. Так как
, где z – новая неизвестная функция. Проинтегрируем уравнение (6.1) описанным методом. Так как  , то
, то 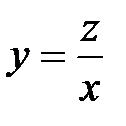 , а следовательно уравнение (6.1) примет вид:
, а следовательно уравнение (6.1) примет вид: .
. , откуда
, откуда  . Последнее равенство определяет общее решение уравнения (6.1).
. Последнее равенство определяет общее решение уравнения (6.1). , (7.1)
, (7.1) и
и  – заданные непрерывные функции от x. Если функция
– заданные непрерывные функции от x. Если функция  , то уравнение (7.1) имеет вид:
, то уравнение (7.1) имеет вид: (7.2)
(7.2) ≢0) оно называется линейным неоднородным уравнением.
≢0) оно называется линейным неоднородным уравнением. ;
; ;
; . (7.3)
. (7.3) так, чтобы общее решение линейного однородного уравнения (7.2) являлось решением неоднородного линейного уравнения (7.1). Тогда производная функции (7.3) примет вид:
так, чтобы общее решение линейного однородного уравнения (7.2) являлось решением неоднородного линейного уравнения (7.1). Тогда производная функции (7.3) примет вид: .
.
 .
. ,
, – произвольная постоянная.
– произвольная постоянная. . (7.4)
. (7.4) 
 . Сформулируем замеченный факт в виде теоремы.
. Сформулируем замеченный факт в виде теоремы. , то все остальные решения имеют вид
, то все остальные решения имеют вид 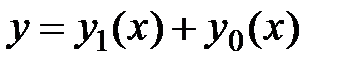 , где
, где  – общее решение соответствующего линейного однородного дифференциального уравнения.
– общее решение соответствующего линейного однородного дифференциального уравнения. . Тогда
. Тогда .
. .
. . (7.5)
. (7.5) .
.  (7.6)
(7.6) ,
,  .
. .
. .
. .
. ,
, ,
,  , называется уравнением Бернулли.
, называется уравнением Бернулли. , разделим обе части уравнения Бернулли на
, разделим обе части уравнения Бернулли на  . В результате получим:
. В результате получим: . (8.1)
. (8.1) . Тогда
. Тогда .
. и перейдем к функции z(x):
и перейдем к функции z(x): ,
, , получим общий интеграл уравнения Бернулли, который легко разрешается относительно y. При
, получим общий интеграл уравнения Бернулли, который легко разрешается относительно y. При  добавляется решение
добавляется решение  . Уравнение Бернулли можно также решать, не делая перехода к линейному уравнению путём подстановки
. Уравнение Бернулли можно также решать, не делая перехода к линейному уравнению путём подстановки  , а применяя метод Бернулли, подробно разобранный в 1.7. Рассмотрим применение этого метода для решения уравнения Бернулли на конкретном примере.
, а применяя метод Бернулли, подробно разобранный в 1.7. Рассмотрим применение этого метода для решения уравнения Бернулли на конкретном примере. . (8.2)
. (8.2)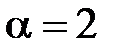 .
. .
. ,откуда
,откуда  . Тогда для функции u(x) получим уравнение:
. Тогда для функции u(x) получим уравнение:  ,или
,или  Последнее уравнение является уравнением с разделяющимися переменными для функции u(x). Решая его, получим:
Последнее уравнение является уравнением с разделяющимися переменными для функции u(x). Решая его, получим: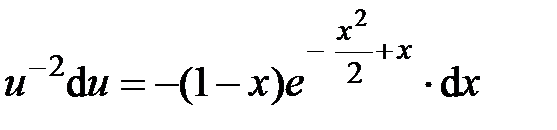 ,
, ,
,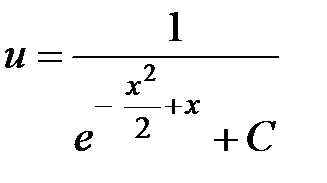 .
. .
. , то оно называется уравнением в полных дифференциалах. Это уравнение можно переписать в виде
, то оно называется уравнением в полных дифференциалах. Это уравнение можно переписать в виде  , следовательно, его общий интеграл есть
, следовательно, его общий интеграл есть  .
.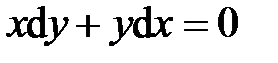 есть уравнение в полных дифференциалах, так как его можно переписать в виде
есть уравнение в полных дифференциалах, так как его можно переписать в виде  . А значит,общий интеграл задаётся равенством
. А значит,общий интеграл задаётся равенством 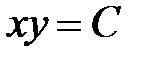 .
. . (9.2)
. (9.2)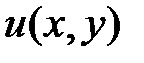 , что
, что  и
и  .
. , то
, то , (9.3)
, (9.3) – произвольная дифференцируемая функция.
– произвольная дифференцируемая функция. .
. , следовательно,
, следовательно,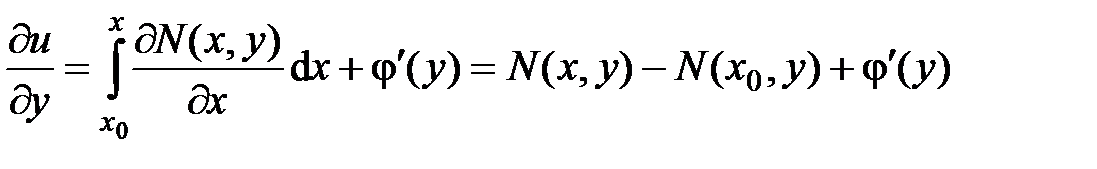 .
. , тогда
, тогда 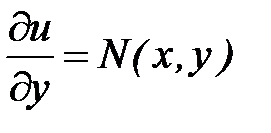 .
.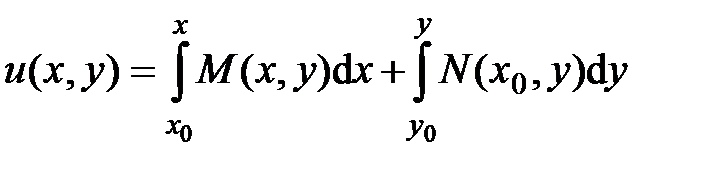 ,
,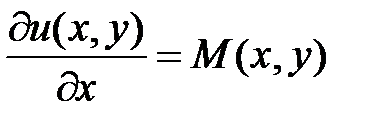 , а
, а  .
.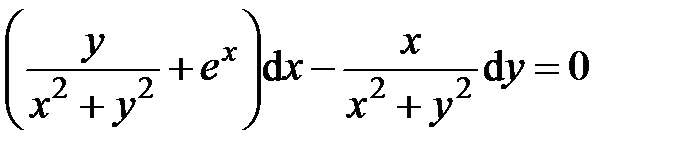 .
.

 .
. и
и  :
: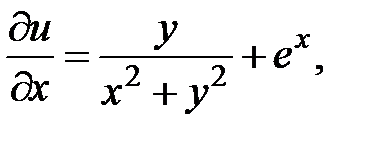
 .
. ,
, .
. :
: .
. и
и  . Следовательно, общим интегралом заданного уравнения является:
. Следовательно, общим интегралом заданного уравнения является:  .
. – такая, что после умножения на неё обеих частей уравнения получающееся дифференциальное уравнение
– такая, что после умножения на неё обеих частей уравнения получающееся дифференциальное уравнение
 , то функция
, то функция  называется интегрирующим множителем исходного уравнения.
называется интегрирующим множителем исходного уравнения. .
. .
. . (10.1)
. (10.1) , где ω – заданная функция от x и y, то уравнение (10.1) сводится к обыкновенному (и притом линейному) уравнению с неизвестной функцией µот независимой переменной ω:
, где ω – заданная функция от x и y, то уравнение (10.1) сводится к обыкновенному (и притом линейному) уравнению с неизвестной функцией µот независимой переменной ω: , (10.2)
, (10.2) ,
, ,
,  .
. ) или только от y (
) или только от y (  ), если выполнены соответственно следующие условия:
), если выполнены соответственно следующие условия:  ,
, 
 ,
,  .
. . (1.1)
. (1.1) и
и  :
: 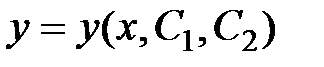 (или
(или  – общий интеграл дифференциального уравнения 2-го порядка). Задача Коши для дифференциального уравнения 2-го порядка (1.1) состоит в отыскании частного решения уравнения, удовлетворяющего начальным условиям: при
– общий интеграл дифференциального уравнения 2-го порядка). Задача Коши для дифференциального уравнения 2-го порядка (1.1) состоит в отыскании частного решения уравнения, удовлетворяющего начальным условиям: при 
 . Необходимо заметить, что графики решений уравнения 2-го порядка могут пересекаться в отличие от графиков решений уравнения 1-го порядка. Однако решение задачи Коши для уравнений 2-го порядка (1.1) при довольно широких предположениях для функций, входящих в уравнение, единственно, т.е. всякие два решения с общим начальным условием
. Необходимо заметить, что графики решений уравнения 2-го порядка могут пересекаться в отличие от графиков решений уравнения 1-го порядка. Однако решение задачи Коши для уравнений 2-го порядка (1.1) при довольно широких предположениях для функций, входящих в уравнение, единственно, т.е. всякие два решения с общим начальным условием  совпадают на пересечении интервалов, на которых определены уравнения.
совпадают на пересечении интервалов, на которых определены уравнения. . Пусть дифференциальное уравнение 2-го порядка имеет вид:
. Пусть дифференциальное уравнение 2-го порядка имеет вид: , (1.2)
, (1.2) . Это позволяет принять
. Это позволяет принять  за новый аргумент, а производную 1-го порядка
за новый аргумент, а производную 1-го порядка 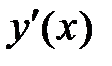 принять за новую функцию
принять за новую функцию  . Тогда
. Тогда
 для функции
для функции  , не содержащее явно
, не содержащее явно  , свелось к уравнению 1-го порядка
, свелось к уравнению 1-го порядка  для функции
для функции 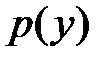 . Интегрируя это уравнение, получаем общий интеграл
. Интегрируя это уравнение, получаем общий интеграл  или
или  , а это есть дифференциальное уравнение 1-го порядка для функции
, а это есть дифференциальное уравнение 1-го порядка для функции 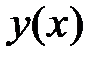 . Решая его, получаем общий интеграл исходного дифференциального уравнения (1.2), зависящий от двух произвольных постоянных:
. Решая его, получаем общий интеграл исходного дифференциального уравнения (1.2), зависящий от двух произвольных постоянных: 
 при заданных начальных условиях:
при заданных начальных условиях: 
 , то примем
, то примем  за новую независимую переменную, а
за новую независимую переменную, а  – за
– за  . Тогда
. Тогда  и уравнение для функции
и уравнение для функции  приобретает вид:
приобретает вид:
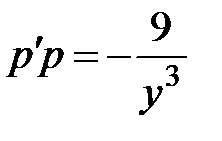 . Отсюда следует
. Отсюда следует  , т.е.
, т.е.  .
.
 и
и  , то подставляя эти данные в последнее равенство, получаем, что
, то подставляя эти данные в последнее равенство, получаем, что  и
и  , откуда
, откуда  . В результате для функции
. В результате для функции  имеем уравнение с разделяющимися переменными, решая которое получаем
имеем уравнение с разделяющимися переменными, решая которое получаем  . Используя начальные условия, получаем, что
. Используя начальные условия, получаем, что  . Следовательно, частный интеграл уравнения, удовлетворяющий начальным условиям, имеет вид:
. Следовательно, частный интеграл уравнения, удовлетворяющий начальным условиям, имеет вид: 
 . Пусть дифференциальное уравнение 2-го порядка имеет вид:
. Пусть дифференциальное уравнение 2-го порядка имеет вид:  , т.е. в уравнение явно не входит искомая функция
, т.е. в уравнение явно не входит искомая функция  . В этом случае вводят подстановку
. В этом случае вводят подстановку  . Тогда
. Тогда 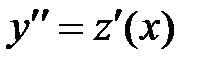 и уравнение 2-го порядка
и уравнение 2-го порядка  для функции
для функции  становится уравнением 1-го порядка
становится уравнением 1-го порядка 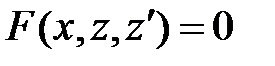 для функции
для функции  . Проинтегрировав его, получаем дифференциальное уравнение 1-го порядка для функции
. Проинтегрировав его, получаем дифференциальное уравнение 1-го порядка для функции  :
: 
 зависящий от двух произвольных постоянных:
зависящий от двух произвольных постоянных:
 .
. , следовательно, делаем замену:
, следовательно, делаем замену:  и
и 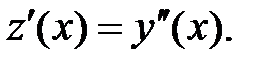 В результате чего получаем дифференциальное уравнение 1-го порядка для функции
В результате чего получаем дифференциальное уравнение 1-го порядка для функции  :
:
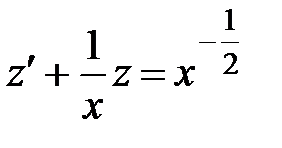 .
.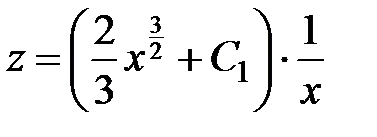
 .
. получили дифференциальное уравнение с разделяющимися переменными:
получили дифференциальное уравнение с разделяющимися переменными: ,
, .
. . Разделяя обе части на
. Разделяя обе части на  получаем
получаем


 .
. , (2.1)
, (2.1)

 и
и  – заданные функции, непрерывные на том промежутке, на котором ищется решение.
– заданные функции, непрерывные на том промежутке, на котором ищется решение. разделим (2.1) на
разделим (2.1) на  и, после введения новых обозначений для коэффициентов, запишем уравнение в виде:
и, после введения новых обозначений для коэффициентов, запишем уравнение в виде: (2.2)
(2.2)
 если на рассматриваемом промежутке функции
если на рассматриваемом промежутке функции  ,
,  и
и  непрерывны.
непрерывны.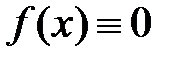 , то уравнение (2.2) называется линейным однородным дифференциальным уравнением (ЛОДУ). В противном случае, т.е. при
, то уравнение (2.2) называется линейным однородным дифференциальным уравнением (ЛОДУ). В противном случае, т.е. при  ≢0, уравнение (2.2) называется линейным неоднородным дифференциальным уравнением (ЛНДУ).
≢0, уравнение (2.2) называется линейным неоднородным дифференциальным уравнением (ЛНДУ). называется выражение
называется выражение  , где
, где  – произвольные числа.
– произвольные числа. и
и  – решения ЛОДУ
– решения ЛОДУ , (2.3)
, (2.3) , где
, где  – произвольные числа,также будет решением этого уравнения.
– произвольные числа,также будет решением этого уравнения. в уравнение (2.3) и покажем, что в результате получается тождество:
в уравнение (2.3) и покажем, что в результате получается тождество:

 и
и  являются решениями уравнения (2.3), то выражения в каждой из скобок в последнем уравнении тождественно равны нулю, что и требовалось доказать.
являются решениями уравнения (2.3), то выражения в каждой из скобок в последнем уравнении тождественно равны нулю, что и требовалось доказать. , что если
, что если  – решение уравнения (2.3), то
– решение уравнения (2.3), то  тоже есть решение этого уравнения.
тоже есть решение этого уравнения. , получим, что сумма двух решений ЛОДУ
, получим, что сумма двух решений ЛОДУ 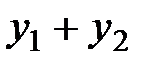 также является решением этого уравнения.
также является решением этого уравнения. это означает, что
это означает, что 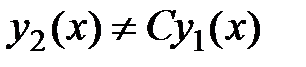 , т.е.
, т.е.  . Последнее условие можно переписать в виде
. Последнее условие можно переписать в виде  ≢0или
≢0или  ≢0. Стоящий в числителе этого выражения определитель
≢0. Стоящий в числителе этого выражения определитель  называется определителем Вронского для функций
называется определителем Вронского для функций  и
и  . Таким образом, определитель Вронского для двух линейно независимых функций не может быть тождественно равен нулю.
. Таким образом, определитель Вронского для двух линейно независимых функций не может быть тождественно равен нулю. – определитель Вронского для линейно независимых решений
– определитель Вронского для линейно независимых решений  удовлетворяет уравнению
удовлетворяет уравнению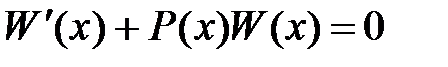 . (3.1)
. (3.1)


 – решение уравнения (3.1). Найдём это решение:
– решение уравнения (3.1). Найдём это решение: ;
; 
 ,
, ,
,  ,
, ,
, 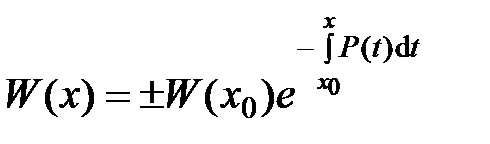 .
. получается тождество. Таким образом,
получается тождество. Таким образом, (3.2)
(3.2)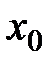 , в которой определитель для линейно независимых решений уравнения (2.3)
, в которой определитель для линейно независимых решений уравнения (2.3)  отличен от нуля. Тогда из формулы Лиувилля следует, что функция
отличен от нуля. Тогда из формулы Лиувилля следует, что функция  будет отлична от нуля при всех значениях
будет отлична от нуля при всех значениях 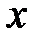 из рассматриваемого промежутка, поскольку при любом значении
из рассматриваемого промежутка, поскольку при любом значении 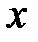 оба множителя в правой части формулы (3.2) отличны от нуля.
оба множителя в правой части формулы (3.2) отличны от нуля.