 ПОЗНАВАТЕЛЬНОЕ
| Визначення молярної маси і густини
Лабораторна робота Визначення універсальної газової сталої методом відкачування
Прилади і матеріали:установка для визначення універсальної газової сталої, аналітичні терези. Завдання: Визначити числове значення універсальної газової сталої. Теоретичні відомості Фізичний зміст універсальної газової сталої. При ізохоричному ( V – const ) нагріванні одного моля газу вся надана йому теплота витрачається на збільшення внутрішньої енергії ΔU. ΔQ = ΔU . Молярна теплоємність газу при сталому об’ємі
де ΔT – збільшення температури газу при нагріванні. При ізобаричному ( р – const ) нагріванні одного моля газу теплота ΔQ витрачається на збільшення внутрішньої енергії ΔU і на роботу розширення газу ΔА, тобто ΔQ = ΔU + ΔА. Молярна теплоємність газу при сталому тиску
де ΔА= рΔV – робота розширення газу. (3) Початковий стан 1 моля газу описується рівнянням Менделєєва – Клапейрона pV = RT. (4) Після нагрівання при p – const на ΔΤ об’єм газу збільшиться на ΔV і рівняння стану набере вигляду p ( V + ΔV) = R ( T+ ΔT). (5) Враховуючи (3) і (4) з (5) отримаємо pΔV = RΔT, тобто ΔА= RΔT; звідки R= Універсальна газова стала R чисельно дорівнює роботі розширення одного моля газу при нагріванні його на 1К при сталому тиску.
В даній роботі універсальна газова стала визначається методом відкачування. Установка складається з балона Б, з якого відкачують газ, насоса Н, яким відкачують та манометра М, який показує тиск газу в балоні після відкачки, з’єднані між собою гумовими трубками. До установки додаються терези для зважування балона з газом при атмосферному тиску і зважування балона після відкачування. Рівняння Менделєєва - Клапейрона для об’єму V, при кімнатній температурі T, атмосферному тиску p1, для маси повітря М1 в балоні Б запишеться так:
де М1 = m1 – m0; m0 – маса самого балона А, m1 – сумарна маса балона Б і повітря в ньому при тиску p1. Якщо відкачати насосом Н повітря із балона Б до тиску p2 (при тій же температурі), то рівняння (1) запишеться так:
де М2 = m2 – m0; m2 – сумарна маса балона Б і повітря в ньому при тиску р2 (після відкачування). Із рівнянь (1) і (2) знаходимо універсальну газову сталу:
Якщо в початковому стані повітря перебуває при атмосферному тиску то манометр має нульові покази. При відкачуванні він показує зміну тиску (р1-р2), яку й потрібно підставляти у співвідношення (3). Відносна похибка вимірювання може бути знайдена з формули (3) методом логарифмування та диференціювання
Хід роботи: 1. На аналітичних терезах зважують балон Б. 2. За допомогою гумової трубки з‘єднують балон Б (з краном К) з манометром і насосом. 3. Насосом Н відкачують повітря із балона Б. 4. Закривають кран К, від’єднують балон Б і на терезах знаходять сумарну масу m2 балона і повітря в ньому (після відкачування). 5. Вимірювання проводять не менше трьох разів при як можна більших значеннях зміни тиску. 6. За формулою (3) обчислюють шукану величину R, а за формулою (4) знаходять відносну похибку. Після цього обчислюють абсолютну похибку результату. Контрольні запитання: 1. Дайте означення молярної маси? 2. Обчисліть молярну масу повітря. 3. В яких одиницях вимірюють тиск та які співвідношення між цими одиницями? 4. Яким вимогам має відповідати модель ідеального газу? 5. Який фізичний зміст універсальної газової сталої? 6. В чому полягає відмінність між рівняннями Клапейрона та Менделєєва – Клапейрона? 7. Обчисліть густину повітря при нормальних умовах. 8. Закрита посудина повністю заповнена водою при 27 0С. Яким би був тиск в посудині, якби сили взаємодії між молекулами води зникли? Лабораторна робота Визначення молярної маси і густини Газу методом відкачування Мета роботи – ознайомлення з одним із методів визначення молекулярної маси і густини газу.
Теоретичні відомості Молярною масою зветься маса одного моля речовини. У СІ ця величина вимірюється в кілограмах на моль. Моль – кількість речовини, яка містить стільки ж структурних елементів (молекул, атомів і т.д.), скільки атомів міститься в ізотопі вуглецю 12С масою 0,012 кг. Молярну масу газу можна визначити з рівняння газового стану. При не дуже високих тисках, але досить високих температурах газ можна вважати ідеальним. Стан такого газу описується рівнянням Менделєєва-Клапейрона:
де Р – тиск газу; V – об’єм газу, m – маса газу; - універсальна газова стала; Т – абсолютна температура газу. З рівняння (1) можна одержати формулу для молярної маси газу:
Якщо вимірювання тиску Р, об’єму V, температури Т газу, тобто параметрів газу, які входять до формули (2), не викликає особливих труднощів, то визначення маси газу виконати практично неможливо, тому що газ можна зважити тільки разом з колбою, в якій він знаходиться. Існує інший спосіб визначення Нехай у колбі об’ємом V знаходиться газ масою m1 під тиском Р1 і за температури Т. Рівняння стану (1) для цього газу має вигляд
Відкачуємо частину газу з колби, не змінюючи його температури. Після відкачування маса газу, що залишився у колбі, та його тиск зменшується. Позначимо їх відповідно m2 і Р2 і знову запишемо рівняння стану
З рівнянь (3) та (4) дістанемо:
Одержана формула (5) дає можливість визначити У даній роботі досліджуваним газом є повітря, яке являє собою суміш азоту, кисню, аргону та інших газів. Формула (5) придатна і для визначення
де Якщо відома молярна маса газу, то можна легко визначити ще одну важливу характеристику газу – його густину
Виразивши
Густину суміші газів можна обчислити за формулою (12.8), розуміючи під
|



 , (1)
, (1) , (2)
, (2) (6)
(6) Метод визначення R і опис установки
Метод визначення R і опис установки , (1)
, (1) , (2)
, (2) (3)
(3) . (4)
. (4) , (1)
, (1) - молярна маса газу; R=8,31 Дж/(моль К)
- молярна маса газу; R=8,31 Дж/(моль К) . (2)
. (2) . (3)
. (3) , (4)
, (4) . (5)
. (5) , (6)
, (6) ,
,  , ...,
, ...,  - відомий зміст кожного газу;
- відомий зміст кожного газу;  ,
,  , ...,
, ..., 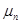 - молярні маси газів.
- молярні маси газів. . Густина газу – це маса одиниці об’єму газу:
. Густина газу – це маса одиниці об’єму газу: . (7)
. (7)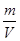 з рівняння Менделєєва – Клапейрона, дістанемо
з рівняння Менделєєва – Клапейрона, дістанемо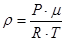 . (8)
. (8)