 ПОЗНАВАТЕЛЬНОЕ
| Географічні (земні) системи координат
Зоряні системи координат включають час і тому не дуже-зручні для визначення положень точок земної поверхні. Так, координати точок земної поверхні в цих системах були б змінними величинами, залежних від часу. Це викликало б деякі труднощі в рішенні різних наукових і практичних задач геодезії. Тому положення точок земної поверхні доцільно визначати в таких системах координат, які б не містили часу. У геодезії застосовують дві системи координат, які обертаються разом з Землею і не включають часу, як системи відліку. Одна з них задається на основі астрономічних спостережень і називається астрономічною системою координат, а інша будується за результатами геодезичних вимірювань і носить назву геодезичної системи координат. Обидві ці системи мають важливе значення для географічного вивчення поверхні Землі і тому можуть бути об'єднані під загальною назвою системи географічних координат. Географічні системи астрономічних і геодезичних координат є особливого роду криволінійними координатами. Якби Земля була ідеальною кулею, то вони перетворилися б в звичайні системи сферичних координат. Для завдання географічної системи астрономічних координат скористаємося раніше введеною системою просторових прямокутних координат х, у, z, яка відповідає першій екваторіальній системі зоряних координат. За основну площину хоу цієї системи в цьому випадку приймемо площину середнього земного екватора відомої епохи. Основну координатну вісь х цієї системи направимо в точку G0 перетину середнього земного екватора з площиною, паралельну площині середнього астрономічного меридіана Грінвича G, що проходить через середню вісь ор обертання Землі прийнятої епохи. Вісь у розташуємо в площині земного екватора під кутом 90° на схід від грінвічського меридіана, а вісь z сумістимо з північним напрямом середньої осі обертання Землі тієї ж епохи. Положення точки земної поверхні відносно основних площин прийнятої системи координат можна охарактеризувати просторовими компонентами напряму прямовисної лінії в цій точці. Вони можуть бути визначені з астрономічних спостережень і називаються астрономічною широтою і довготою точки, що розглядається. Астрономічна широта φ точки М земної поверхні рівна куту, утвореному прямовисною лінією в цій точці з площиною хоу земного екватора. Астрономічна довгота λ точки, що розглядається М рівна двогранному куту між площиною p'o'M0' меридіана цієї точки і площиною роG0 початкового меридіана (рис. 2.6).
Рис. 2.6. Астрономічна система координат Астрономічні широти відлічують від земного екватора - північніше від нього зі знаком плюс і на південь зі знаком мінус - від 0 до 90°. Астрономічні довготи в астрономії відлічують від початкового меридіана - західніше від нього зі знаком плюс і на схід зі знаком мінус - від 0 до 180° або в часовій мірі від 0 до 12h. Однак потрібно мати на увазі, що в геодезії астрономічні довготи відліковують від того ж початкового меридіана, але із зворотними знаками, чим це прийнято в астрономії. Щоб повністю охарактеризувати астрономічну систему координат в кожній даній точці земної поверхні, необхідно ще визначити в цій точці напрям місцевого меридіана. Це досягається тим, що в даній точці визначають астрономічний азимут напряму на яку-небудь суміжну закріплену точку земної поверхні. При цьому під астрономічним азимутом а напряму МК в даній точці М розуміють двогранний кут між площиною p'o'M'0 місцевого астрономічного меридіана і прямовисною площиною, проведеною в топоцентрі М через точку К земної поверхні (див. рис. 2.6). Астрономічні азимути прийнято відлічувати в астрономії від точки півдня, а в геодезії від точки півночі по ходу годинникової стрілка від 0 до 360°. Оскільки дійсна фігура Землі відрізняється від фігури обертання, то астрономічні координати неможливо виразити через кутові величини, виміряні на земній поверхні і віднесені безпосередньо до екватора і земного полюса. Проте доповнення астрономічної широти даної точки до прямого кута звичайно ототожнюють з кутом між прямовисною лінією в цій точці і віссю обертання Землі або паралельної їй віссю небесної сфери, відносячи цей кут до площини місцевого меридіана. Відмітимо тут, що точки перетину земної поверхні з віссю обертання Землі є астрономічними полюсами Землі. Відповідно до цього доповнення астрономічної широти даної точки до прямого кута прийнято називати полярною відстанню точки, або висотою полюса. Як вже було сказано, прямовисні лінії в точках земної поверхні не тільки не проходять через центр маси Землі, але навіть не перетинають її вісь обертання. Площини місцевих меридіанів в загальному випадку також не проходять через вісь обертання Землі, а лише паралельні їй. Тому земна астрономічна система координат не задовольняє умовам геоцентричності. Взагалі кажучи, астрономічні координати φ, λ можна було б перетворювати в геоцентричні величини Ф, Л. Тоді положення будь-якої точки земної поверхні визначилося б її геоцентричними сферичними координатами Д, Ф, Л, від яких, застосовуючи формули (2.16), легко можна було б перейти і до просторових прямокутних координат. Але для перетворення астрономічних координат кожної даної точки в геоцентричні величини, а також для визначення геоцентричного радіуса-вектора цієї точки необхідні точні дані про фігуру і розміри проходячої через неї рівенної поверхні Землі. Через рух астрономічних полюсів Землі пов'язана з нею астрономічна система координат безперервно коливається відносно свого деякого середнього положення. Тому отримані з безпосередніх астрономічних спостережень широта і довгота, а також і азимут в даній точці земної поверхні відносяться до миттєвого положення полюса і характеризують її положення в тій миттєвій системі координат, якій відповідає моменту або епосі цих спостережень (див. рис. 2.4).
 Рис. 2.7. Коливання полюса Звідси виникає задача про приведення астрономічних широт, довгот і азимутів, визначених в різних точках і в різні епохи, до вибраного нерухомого полюса або до відповідної єдиної епохи, для якої задається пов'язана з Землею нерухома система астрономічних координат. Для перетворення астрономічних координат φ, λ і азимута а, пов'язаних з миттєвим полюсом р, в астрономічні координати φ, λ, і азимут а, віднесені до нерухомого полюса р, з даної точки М опишемо допоміжну сферу. На цій допоміжній сфері намітимо зеніт даної точки і проведемо сліди площин, паралельних відповідно площинам миттєвих і середніх місцевих і початкових меридіанів (мал. 2.7). При цьому будемо передбачати, що спостережені і приведені довготи відлічуються, як це прийняте в цей час, від миттєвого і середнього меридіанів точки перетину середнього початкового меридіана зі середнім екватором, так що
Приймемо, що положення миттєвого полюса р в момент астрономічних спостережень характеризується його прямокутними сферичними координатами хр, ур відносно їх початку в середньому полюсі р іїх осей, направлених відповідно по середньому початковому меридіану на південь і перпендикулярно від нього на захід, Приймемо також, що довготи позитивні на захід і негативні на схід від початкового меридіана.
Рис. 2.8. Геодезична система координат Вирішуючи показані на мал. 2.7 сферичні трикутники, остаточно отримаємо
При побудові географічної системи геодезичних координат фігуру Землі звичайно приймають за деякий еліпсоїд обертання з відомими розмірами і заданим положенням в тілі Землі. Розміри і положення цього еліпсоїда, який прийнято називати референц-еліпсоїдом, прагнуть встановити так, щоб він можливо краще представляв фігуру геоїда. При цьому прагнуть також, щоб центр і мала вісь референц-еліпсоїда співпадали відповідно з центром маси і віссю обертання Землі. Однак по ряду причин, які будуть пояснені надалі, ці основні умови побудови геоцентричної системи геодезичних координат в загальному випадку не виконуються. Система геодезичних координат також може бути задана у вигляді просторових прямокутних Х, Y, Z, початок яких суміщений з центром О референц-еліпсоїда і основною площиною XOYякою служить площина його екватора. При цьому доцільно за координатну вісь Х прийняти лінію перетину площин екватора референц-еліпсоїда і відповідним чином вибраного геодезичного початкового меридіана, вісь Y розташувати в площині екватора під кутом 90° від початкового меридіана і вісь Z направити на північ по малій осі ОР референц-еліпсоїда (рис. 2.8). Потрібно зазначити, що положення початкового геодезичного меридіана відносно початкового ж астрономічного меридіана залежать від умов орієнтування референц-еліпсоїда в тілі Землі. Зв'язок між просторовими прямокутними координатами в астрономічній і геодезичній системах виражається відомими формулами взаємного їх перетворення. Сумістивши початки цих систем координат шляхом паралельного перенесення їх осей, із їх загального початку опишемо допоміжну сферу, на якій покажемо кути Ейлера, а саме кути прецесії ψ, власного обертання τ і нутації θ, що характеризують взаємне орієнтування відповідних осей координат (мал. 2.9).
Рис. 2.9. Зв'язок між астрономічною і геодезичною системами просторових прямокутних координат
При перетворенні геодезичної системи прямокутних координат X, Y, Z в астрономічну систему аналогічних координат х у, z братимемо до уваги, що початки цих систем координат в загальному випадку не співпадають. Нехай Δх0, Δу0, Δz0 -координати центра О референц-еліпсоїда в астрономічній системі і ΔХ0, ΔY0, ΔZ0 - координати центра o маси Землі в геодезичній системі. Тоді для переходу від геодезичної системи прямокутних координат до астрономічної, тобто до геоцентричної системи, можна написати співвідношення
і для зворотного переходу будемо мати наступні вирази:
Вхідні в ці вирази направляючі косинуси кутів між осями систем координат, що розглядаються виражаються через Ейлерові кути формулами
Ейлерові кути φ, τ і θ разом з величинами Δх0, Δу0, Δz0 або ΔХ0, ΔY0, ΔZ0 цілком визначають положення і орієнтування референц-еліпсоїда в тілі Землі. З формул (2.20) можна бачити, що відповідні осі астрономічної і геодезичної систем прямокутних координат будуть взаємно паралельні тільки в тому випадку, коли Ейлерові кути будуть рівні нулю. Для супутникової геодезії система просторових прямокутних координат має дуже важливе значення. Вона знаходиться в прямій або навіть природній відповідності до характеру і складу величин, що вимірюються при спостереженнях супутників. Однак в геодезії досить широко застосовують географічну систему геодезичних координат, в основі якої також лежить референц-еліпсоїд, в тій або іншій мірі характеризуючого фігуру і розміри Землі. У географічній системі геодезичних координат положення точок простору, включаючи і земну поверхню, характеризують їх геодезичними широтами, довготами і висотами. Геодезична широта В точки М рівна куту, утвореному нормаллю MN до поверхні референц-еліпсоїда в цій точці з площиною XOY його екватора. Геодезична ж довгота L точки М рівна двогранному куту між площинами місцевого геодезичного меридіана РОМ і початкового геодезичного ж меридіана POX. Геодезична висота Н точки рівна відстані М'М від поверхні референц-еліпсоїда до цієї точки (див. мал. 2.8). Крім перерахованих характеристик положення точки, в ній необхідно ще вказати напрям місцевого геодезичного меридіана, тобто вказати геодезичний азимут напряму на яку-небудь суміжну фіксовану точку. Потрібно зазначити, що геодезичні широти і довготи, а також азимути і висоти не можуть бути визначеними із безпосередніх спостережень і вимірювань. Звичайно їх отримують шляхом складної математичної обробки геодезичних вимірювань, приводячи їх до поверхні прийнятого референц-еліпсоїда. Іноді положення точки, що розглядається в геодезичній системі координат визначають також її відповідними сферичним координатами, а саме її радіусом-вектором R' відносно центра референц-еліпсоїда, сферичною широтою Ф' і сферичною довготою L'. При цьому сферична довгота точки в геодезичній системі координат рівна безпосередньо її геодезичній довготі L (див. мал. 2.8). Сферичну широту Ф' в геодезії звичайно прийнято називати геоцентричною широтою, хоч вона в загальному випадку такою широтою і не є. Сферичні координати R', Ф', L' = L в геодезичній системі будуть геоцентричними координатами тільки в тому випадку, коли центр і мала вісь референц-еліпсоїда співпадають відповідно з центром маси і віссю обертання Землі. Між просторовими прямокутними і криволінійними координатами точки в геодезичній системі існують відомі прості співвідношення
де N - радіус кривизни першого вертикала, який через велику напіввісь а і ексцентриситет е еліпсоїда виражається формулою
Звідси можна написати зворотні співвідношення, які будуть мати трохи більш складний вигляд
Легко бачити, що геодезична широта по просторовим прямокутним координатам точки може бути обчислена тільки методом послідовних наближень. Хоч ці наближення сходяться досить швидко,
Рис. 2.10. Зв'язок між астрономічними і геодезичними координатами все ж краще за їх виконати аналітичним способом. Так, користуючись відомими висновками для обчислення геодезичної широти можна написати формулу
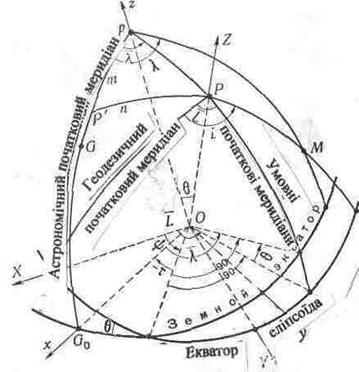
Для розв'язання наукових і практичних питань геодезії необхідно знати зв'язки між відповідними географічними координатами в астрономічній і геодезичній системах. Щоб встановити ці зв'язки, з даної точки М земної поверхні опишемо допоміжну сферу (рис. 2.10). Продовження нормалі MZg до поверхні референц-еліпсоїда і прямовисної лінії Mza вцій точці перетнуть допоміжну сферу в точках Zg і Za, відповідних геодезичному і астрономічному зеніту. Далі в даній точці М проведемо напрями МР і Мр, паралельні відповідно малій осі референц-еліпсоїда і осі обертання Землі що перетинають допоміжну сферу в точках P і p, які представляють геодезичний і астрономічний полюси. У тій же точці М проведемо ще напрям МК насуміжну з нею точку К, геодезичний і астрономічний азимути якої підлягають зіставленню. Площини геодезичного і астрономічного меридіанів даної точки М перетнуть допоміжну сферу по дугах великих кіл ZgP і Zap, а дуги великих кіл ZgK і ZaK будуть слідами нормальної і прямовисної площин, проведених в цій точці через точку, що спостерігається К.Провівши в точці, що розглядається М площину MzaP, на допоміжній сфері отримаємо дугу великого кола ZaP, яке можна назвати геодезичним меридіаном астрономічного зеніту цієї точки. Відповідно до цього введемо поняття про геодезичну широту В' і довготу L' астрономічного зеніту, а також про геодезичний азимут А' напряму МК при астрономічному зеніті даної точки. На допоміжній сфері проведемо також дуги великих кіл, що представляють геодезичний і астрономічний початкові меридіани, від яких відлічуються відповідні довготи. Хоч у загальному випадку осі обертання Землі і референц-еліпсоїда взаємно не паралельні, але завжди існує один астрономічний і один геодезичний меридіани, площини яких взаємно паралельні. Сліди площин цих меридіанів на допоміжній сфері зливаються і утворюють дугу великого кола Рр, на якій лежать астрономічний і геодезичний полюси. Ця обставина дає просту можливість для приведення астрономічних і геодезичних довгот до взаємно паралельних початкових меридіанів, тобто на один умовний початок рахунку довгот. Для цього досить з всіх астрономічних і всіх геодезичних довгот відняти відповідно астрономічну довготу λ і геодезичну довготу L взаємно паралельних меридіанів. Дуга великого кола Рр, відповідна куту θ між осями обертання Землі і референц-еліпсоїда, а також астрономічна довгота λ цього кола є полярними сферичними координатами геодезичного полюса Р відносно астрономічного полюса р і початкового астрономічного меридіана. Вони можуть бути замінені прямокутними сферичними координатами т і п з початком в астрономічному полюсі р і з осями, направленими по початковому астрономічному меридіану до Грінвічу і перпендикулярно від нього на схід (рис. 2.10). Передбачуючи, що ці координати є малими дугами, їх можна виразити простими співвідношеннями
При незмінному орієнтуванні референц-еліпсоїда в тілі Землі величини т, п і θ залишаються постійними. Надалі буде показано, що вони залежать від помилок встановлення початкових геодезичних дат і можуть бути перетворені в Ейлерові кути і навпаки. Кут u між нормаллю до поверхні референц-еліпсоїда і прямовисною лінією в даній точці прийнято називати повним схиленням прямовисної лінії. Звичайно цей кут розкладають на дві його складові ξ і η відповідно в площинах меридіана і першому вертикалі. Схилення прямовисних ліній залежать від помилок як в розмірах, так і в орієнтуванні прийнятого референц-еліпсоїда. Але все ж вони є малими величинами, квадратами яких майже завжди можна нехтувати. Повне схилення виска u ігеодезичний азимут а площини, в якій він лежить, представляють сферичні полярні координати астрономічного зеніту точки відносно її геодезичного зеніту. Складові ж схилення виска в площинах меридіана і першому вертикалі будуть сферичними прямокутними координатами астрономічного зеніту і визначаться за формулами
Спочатку встановимо зв'язок між геодезичними координатами і азимутами в даній точці і в її астрономічному зеніті. Вирішуючи прямокутний сферичний трикутник QzaP і не приводячи подробиць, будемо мати
З вирішення ж сферичних трикутників ZgZaP і ZgZaK спочатку отримаємо співвідношення
Визначаючи з цих співвідношень геодезичний азимут, отримаємо вираз
Оскільки зенітні відстані точок земної поверхні в більшості випадків близькі до 90°, а складові схиляння виска рідко досягають 30", то цей вираз практично можна застосовувати без його останнього члена
Далі встановимо зв'язок астрономічних координат і азимута в даній точці з геодезичними координатами і азимутом в її астрономічному зеніті. З вирішення сферичного трикутника ZaPp і вхідних в нього прямокутних трикутників zаPp і p'Pp знайдемо вирази
Нагадавши, що величини λ і L є довготами астрономічного і геодезичного меридіанів, площини яких взаємно паралельні, введемо позначення
Використовуючи прямокутні сферичні координати геодезичного полюса відносно астрономічного полюса, вираз (2.26) представимо у вигляді
Підставляючи ці вирази в формули (2.24) і (2.25), отримаємо остаточні співвідношення між відповідними географічними координатами і азимутами в геодезичній і астрономічній системах
Ці формули виражають впливи схилень прямовисної лінії на астрономічні широти, довготи і азимути в тому загальному випадку, коли осі обертання Землі і референц-еліпсоїда взаємно не паралельні. Виключивши з другої і третьої рівності (2.27) складову схилення виска в першому вертикалі, отримаємо так звану умову Лапласа в загальному вигляді
Якби осі обертання Землі і референц-еліпсоїда були взаємнопаралельні, то на допоміжній сфері (див. рис. 2.10) астрономічний і геодезичний полюси, а також відповідні початкові меридіани співпали б один з одним. У цьому частковому випадку співвідношення (2.27) перетворилися б в добре відомі класичні формули
У цьому випадку умова Лапласа (2.28) прийняла б той простий вигляд, в якому вона звичайно застосовується
Виконання умови Лапласа в цій формі служить найбільш важливим доказом взаємної параллельности осі обертання Землі і референц-еліпсоїда. Формули (2.27) (2.30) поки виведені в припущенні, що вхідні в них астрономічні широти, довготи і азимути, а також складові схилення виска вільні від тих або інших можливих помилок їх визначення. При будь-якому орієнтуванні референц-еліпсоїда різниця геодезичної і астрономічної зенітних відстаней напряму виражається однією і тією ж формулою, яку можна отримати з вирішення сферичного трикутника ZgzaK і яка має вигляд
Задане орієнтування референц-еліпсоїда визначає і систему геодезичних висот Н, що представляють суму нівелірних висот h і їх аномалій ξ, тобтовідступів геоїда або квазігеоїида від поверхні референц-еліпсоїда
Геодезична висота точки входить до складу її геодезичних координат, а нівелірну висоту точки можна включити до складу її астрономічних координат. Для орієнтування референц-еліпсоїда в тілі Землі досить геодезичні координати B0, L0, Н0 і азимут А0 в якій-небудь одній точці О земної поверхню поставити в той або інший зв'язок з астрономічними координатами φ0, λ0, h і азимутом a0 в цій точці. Зазвичай цю точку приймають за початковий пункт астрономо-геодезичної мережі, а геодезичні координати і азимут в ній називають початковими геодезичними датами. У найпростішому випадку для орієнтування референц-еліпсоїда геодезичні координати і азимути в початковому пункті приймають рівними відповідним астрономічним величинам. У загальному ж випадку в початковому пункті визначають не тільки астрономічні координати і азимут, але і складові схилення виска і аномалію нівелірної висоти, маючи на увазі початкові геодезичні дати підпорядкувати співвідношенням (2.29) і (2.32). Але ці співвідношення, що виражають умову паралельності осей обертання Землі і референц-еліпсоїда, можуть не виконуватися в їх суворій формі через неминучі помилки визначення перерахованих величин. Так, помилка δφ0 визначення астрономічної широти φ0 в початковому пункті зміщає його істинний зеніт відносно земного полюса в площині місцевого меридіана. Помилка δφ0 про астрономічної довготи λ0 спричиняє відповідне зміщення зеніту в площині першого вертикала, але її можна прийняти і за зміну початку рахунку астрономічних довгот. Помилка ж δа0 визначення астрономічного азимута а0 вибраного напряму в початковому пункті викликає поворот площини місцевого астрономічного меридіана біля прямовисної лінії відносно цього напряму і деяку зміну початку рахунку довгот. Розглянемо вплив помилок астрономічної широти, довготи і азимута, а також складових ухиляння виска в початковому пункті на напрям малої осі референц-еліпсоїда відносно осі обертання Землі. Виходячи з умов паралельності осей обертання Землі і референц-еліпсоїда, тобто з співвідношень (2.29), і беручи до уваги можливі помилки визначення астрономічних величин, а також і складових ухиляння виска, напишемо вирази початкових геодезичних дат
Вхідні в ці вирази помилки астрономічних і геодезичних широт і довгот пов'язані між собою співвідношеннями
Сумарні помилки початкової геодезичної широти і довготи спричиняють лише відповідно поступальне переміщення референц-еліпсоїда в площинах меридіана і паралелі початкового пункту. Крім того, помилка початкової геодезичної висоти спричиняє поступальне переміщення реферепц-еліпсоїда по нормалі до його поверхні в початковому пункті. Але при цих поступальних рухах референц-еліпсоїда зміни геодезичного азимута і довготи повинні бути пов'язані умовою
Передбачаючи, що невиконання цієї умови може викликати перекіс малої осі референц-еліпсоїда відносно осі обертання Землі, і застосовуючи формули (2.27), початкові геодезичні дати представимо у вигляді
Порівнюючи відповідні співвідношення (2.33) і (2.36) і використовуючи вирази (2.34) і (2.35), отримаємо рівняння
Вирішуючи ці рівняння відносно компонентів перекосу малої осі референц-еліпсоїда, остаточно будемо мати
Підставляючи ці величини в умову Лапласа загального вигляду (2.28), що відноситься до початкового пункту, отримаємо формулу
Ця формула виражає умову Лапласа загального ж вигляду, коли осі обертання Землі і референц-еліпсоїда не паралельні. Вираз (2.37) наочно показує, що взаємний перекіс осей обертання Землі і референц-еліпсоїда викликається тільки невиконанням умови
Оскільки помилки визначення астрономічної довготи і азимута в початковому пункті незалежні один від одного, то ця умова в загальному випадку дійсно може бути і не виконана. Зрозуміло, що величини (2.37) характеризують взаємне орієнтування геодезичної і астрономічної систем просторових прямокутних координат. Їх можна досить просто перетворити в косинуси напряму осей названих систем координат. Для цього сумістимо початки обох систем координат шляхом паралельного перенесення їх осей і опишемо допоміжну сферу, зображену на мал. 2.11 і що не вимагає особливих пояснень.
Рис. 2.11. Зв'язок між астрономічною і геодезичною системами географічних координат Тоді для Ейлерових кутів легко отримаємо прості вирази
Замінивши в формулах (2.20) Ейлерові кути їх виразами і відкинувши квадрати малих величин (2.37), косинуси напрямків осей астрономічної і геодезичної систем просторових прямокутних координат можна привести до вигляду
Якщо направляючі косинуси, що входять в матрицю (2.18) замінити їх виразами (2.39) і ввести позначення
то зв'язки між астрономічною (геоцентричної) і геодезичною системами просторових прямокутних координат приймуть більш просту і зручну форму
Нагадаємо, що Δх0, Δу0, Δz0 представляють координати центра референц-еліпсоїда в астрономічній системі координат. Координати ж X, Y, Z просторової точки в геодезичній системі обчислюються по формулах (2.21). Величини δХ, δY, δZ є їх малими поправками, що залежать від перекосу полярної осі референц-еліпсоїда відносно осі обертання Землі. Системи часу Коли кажуть про час в науково-технічному значенні, то необхідно мати на увазі, що цим словом позначають різні поняття. З одного боку, воно означає момент події, явища або дій, тобто власне точку на якій-небудь впорядкованій шкалі часу. З іншого боку, під цим словом мають на увазі проміжок часу між моментами подій, відміченими по одній і тій же шкалі. Нарешті, з поняттям про час пов'язаний збіг моментів подій по якій-небудь навіть довільній шкалі часу. Збіг же моментів подій прийнято називати синхронністю подій. Якщо для повного позначення моменту часу необхідно указати день, місяць і рік, то тоді його називають датою. Але в астрономії умовний початковий момент часу, що служить для завдання початку системи відліку і мати значення дати, прийнято називати епохою. У цьому відношенні астрономічне поняття про епоху відрізняється від звичайного значення цього слова, коли воно означає проміжок часу тієї або іншої тривалості. У рівняння геоцентричного руху супутників входить рівномірно поточний час, який є незалежною змінною і служить свого роду четвертою координатою. Але відповідні спостереження і вимірювання для вивчення рухів супутників і для вирішення задач супутникової геодезії виконують на наземних станціях, положення яких задано в тій або іншій системі координат, пов'язаній з Землею. При цьому напрямок осей заданої системи координат відносно нерухомих зірок, а також взаємні положення станцій і супутників безперервно міняються через обертання Землі біля осі. Тому при спостереженнях супутників передусім виникає задача по визначенню кутів повороту Землі за ті або інші проміжки часу. Кути повороту Землі біля осі обертання можна виразити через видимі переміщення точки (істинної або середньої) весняної рівнодії по екватору або точки перетину екватора з початковим меридіаном. Переміщення ж цих точок можуть бути визначені по спостереженнях видимих рухів зірок на небесній сфері. Це вимагає застосування єдиної системи вимірювання часу, пов'язаною з обертанням Землі можливо простою залежністю. Спостереження супутників для вирішення наукових і практичних задач геодезії вимагає реєстрації моментів часу з дуже високою точністю. Так, помилка в 0,1 мс в реєстрації моменту спостережень супутника відповідає зміні його положення на орбіті приблизно на 0,8 м. Більш докладні міркування про необхідну точність реєстрації часу при спостереженнях супутників будуть викладені пізніше. Для створення системи вимірювання і числення часу використовують природні і штучні явища, що повторюються з можливо постійною періодичністю. У астрономії застосовують три природних системи вимірювання часу, а саме системи всесвітнього часу і зоряного часу, пов'язані з обертанням Землі біля осі, і систему ефемеридного часу, засновану на геоцентричному русі Місяця і геліоцентричних рухах Землі і інших планет. Але в останні роки як в астрономії, так і в інших галузях науки і техніки широке застосування отримала штучно створена система атомного часу, в якій використана періодичність електромагнітних коливань при змінах енергетичного стану атомів того або іншого елемента. Проміжок часу між двома послідовними однойменними кульмінаціями центра видимого диска Сонця на даному меридіані називається істинними добами. Але істинне Сонце рухається по екліптиці, а не по екватору і до того ж нерівномірно, так що зміни його часового кута і відповідні проміжки істинного сонячного часу не пропорційні кутам повороту Землі біля осі. Тому його замінюють середнім екваторіальним сонцем, тобто уявною точкою, яка рухається по екватору рівномірно і пряме сходження якої в кожний даний момент дорівнює середній довготі Сонця. Проміжок часу між двома послідовними кульмінаціями середнього екваторіального сонця на даному меридіані називається середніми сонячними добами і служить основною одиницею всесвітнього часу. Середню довготу Сонця і рівне їй пряме сходження середнього екваторіального сонця на даний момент часу обчислюють по формулі
У цій формулі перший член правої частини рівний прямому сходженню середнього екваторіального сонця, встановленому Н’юкомом для фундаментальної епохи 1900, січ. 0,12h, "а Т - середній сонячний час, що протік від цієї епохи до даного моменту і виражений (як тут, так і надалі ) в тропічних сторіччях. Проміжок часу між двома послідовними кульмінаціями точки весняного рівнодення на даному меридіані називається зоряними добами. Якщо при цьому мається на увазі істинна або середня точка весняного рівнодення, то виходять відповідно істинні або середні зоряні доби. Істинний або середній зоряний час в даній точці, тобто відповідний місцевий зоряний час, вимірюється часовим кутом істинної або середньої точки весняного рівнодення. Відповідний же місцевий зоряний час на початковому астрономічному меридіані прийнято називати грінвічським зоряним часом. Оскільки істинний зоряний час нерівномірний, то він незручний і навіть непридатний для вимірювання проміжків часу. Тривалість одного повного видимого обертання істинного Сонця навколо Землі відносно напряму на одну і ту ж зірку називається зоряним, або сидеричним, роком. Його тривалість, виражена в середніх сонячних добах d визначається формулою сидеричний рік =365,25636042d+0,0000001d Т. Проміжок часу між двома послідовними проходженнями центра істинного Сонця через середню точку весняного рівнодення складає так званий тропічний рік. Його тривалість виражається формулою тропічний рік = 365,24219879 d – 0,00000614 dТ. Оскільки календарний рік повинен бути близький до тропічного року і складатися з цілого числа діб, то будь-який сонячний календар містить роки по 365 і 366 діб. Так, в юліанському календарі (старий стиль літочислення) три послідовно йдучих простих року містять по 365 діб, а наступний за ними так званий високосний рік складається з 366 діб, причому високосним є рік, номер якого ділиться на чотири. Тому середня тривалість юліанського року рівна 365,25 діб, тобто довше тропічного року на 0,0078 діб. Але в григоріанському календарі (новий стиль), введеному в 1582 р. і заснованому на більш точній тривалості тропічного року, високосними вважаються тільки ті з сторічних років, число сотень в номері яких ділиться на чотири (1600, 2000, 2400,. .. ). У цьому випадку середня тривалість календарного року рівна 365,2425 добам, тобто. довше тропічного року всього лише на 0,0003 діб. Змінений на 12h часовий кут істинного Сонця або середнього екваторіального сонця відносно місцевого меридіана з астрономічною довготою, що відлічується від грінвічського меридіана, називається відповідно істинним або середнім сонячним часом. Різниця Е істинного і середнього сонячного часу називається рівнянням часу і у вигляді «рівняння часу Е + 12h» на початок кожних діб календарного року приводиться в «Астрономічному щорічнику». Місцевий середній сонячний час на початковому меридіані, довгота якого рівна нулю, прийнято називати всесвітнім часом. Система всесвітнього часу позначається TU і служить шкалою часу для реєстрації моментів спостережень небесних тіл. Між всесвітнім часом М і грінвічським зоряним часом S існує співвідношення
в якому Всесвітній час і грінвічський зоряний час в один і той же фізичний момент можна виразити через місцевий середній сонячний час т і місцевий зоряний час s на меридіані з астрономічною довготою λ від Грінвіча формулами М=т+ λ; S=s+ λ. У цих формулах астрономічна довгота місця вважається позитивною на захід від Грінвича. Проміжки середнього часу т і зоряного часу s між одними і тими ж фізичними моментами в одній і тій же відповідній шкалі часу пов'язані між собою простими співвідношеннями т = (1 - v) s; s = (l+μ)m; μ = 1/365,24219879 =0,0027379093; v = 1/366,24219879 =0,0027304336. Редукційні величини μm і vs для перекладу середнього часу в зоряний і зворотньо приводяться в «Астрономічному щорічнику». На точність визначення шкали часу шляхом астрономічних спостережень впливають коливання Землі на її осі обертання, тобто рух земних полюсів, а також сезонні і вікові зміни швидкості обертання Землі, викликані різними причинами. Систему часу, яка виходить з безпосередніх астрономічних спостережень, прийнято позначати TU0. Вона залежить від положення станцій спостереження на земній поверхні і не є рівномірною. Тому шкала часу TU0 не може служити мірою кутів повороту Землі біля осі обертання. Міжнародне бюро часу визначає і публікує в своїх щомісячних циркулярах поправки Δλ за рух миттєвого полюса відносно умовного міжнародного початку. Використовуючи ці поправки, отримують систему всесвітнього часу TU1 за формулою TU1=TU0+ Δλ Шкала всесвітнього часу TU1 досить рівномірна. Важлива її перевага полягає в тому, що вона є мірою геометричних кутів повороту Землі біля осі обертання. Тому вона повинна застосовуватися і застосовується в супутниковій геодезії, а також і в навігації. У щомісячних циркулярах Міжнародного бюро часу публікуються також поправки ΔТs, за сезонні зміни швидкості обертання Землі. Використовуючи ці поправки, отримують ще одну шкалу всесвітнього часу TU2 за формулою TU2 = TU1 + ΔТs = TU0 + Δλ + ΔТs. Майбуть, система всесвітнього часу TU2 є найкращим наближенням до рівномірної шкали часу, яку можна отримати астрономічними методами. Рівномірність її може порушуватися тільки можливими нерегулярними і віковими змінами швидкості обертання Землі, які поки мало вивчені. Нерівномірність обертання Землі біля осі викликає коливання тривалості зоряних діб, а також і відповідної секунди, що є основною фізичною одиницею часу і рівної 1/86400 частини цих діб. Це і спонукало ввести особливу рівномірну шкалу часу, названу системою ефемеридного часу і позначається ТЕ. Вона заснована не на обертанні Землі біля осі, а на гравітаційній теорії руху небесних тіл сонячної системи. Тривалість ефемеридной секунди встановлена зазделегідь і дорівнює 1/31556925,9747 частині тропічного року вказаної вище фундаментальної епохи. Вона пов'язана з системою всесвітнього часу TU за формулою TE=TU+ΔТ. Величину ΔТ, що входить в цей вираз називають поправкою за ефемеридний час і визначають із спостережень Місяця. Для цього ефемеридні положення Місяця, обчислені на основі гравітаційної теорії його руху, порівнюють з його ж спостереженими положеннями. При цьому моменти спостереження Місяця реєструють по шкалі всесвітнього часу. У цей час ефемеридні положення Місяця визначають по виправленій теорії Брауна його геоцентричного руху. Нерівномірність систем часу, заснованих на обертанні Землі біля осі і обертанні її навколо Сонця, а також неможливість швидкого визначення ефемеридного часу обумовили створення системи атомного часу, заснованої на періодичності електромагнітних випромінювань при енергетичних переходах атомів того або іншого елемента. Стійка періодичність і швидке відтворення цього явища привели до того, що система атомного часу поступово перетворилася в основну систему вимірювання проміжків часу у всіх областях науки і техніки, включаючи і астрономію. Введення шкали атомного часу змінило навіть погляди на природні системи часу, які залишилися мірою осьового обертання і орбітального руху Землі, але перестали задовольняти сучасним вимогам високоточного визначення проміжків часу. Сучасна шкала атомного часу, яку прийнято позначати ТА, заснована на застосуванні високостабільних атомних еталонів частоти біля 10 обсерваторій або лабораторій часу, що належать різним країнам і пов'язаних з Міжнародним бюро часу. Вона встановлена під умовою, щоб тривалість секунди в системі ТА по можливості була близька до секунди ефемеридного часу. Відповідно до міжнародних визначень і рішень за 1 атомну секунду прийнятий проміжок часу, який рівний 9 192 631 770 періодам випромінювання, відповідного резонансній частоті переходу між двома надтонкими рівнями основного стану атому цезія-133. Цей проміжок часу відповідає тривалості однієї ефемеридної секунди з точністю до 2•10-9. Існує декілька шкал атомного часу. З 1 січня 1966 р. введена шкала ТА (нова шкала A3), що представляє середньовагову шкалу, обчислену за показанням атомних часів обсерваторій і лабораторій часу, які пов'язані з Міжнародним бюро часу. Вона встановлюється так, щоб була по можливості близька до шкали всесвітнього часу TU2. Шкали атомного часу ТА і всесвітнього часу TU2 пов'язані між собою через проміжну шкалу, яка називається шкалою всесвітнього координованого (узгодженого) часу TUC і в якій ведеться передача радіосигналів часу. У колишньому СРСР була прийнята шкала атомного часу ТА1, яка заснована на свідченні двох кварцових годинників, регульованих цезієвим еталоном частоти. Нуль-пункт її співпадає з моментом 1964, січ. 1, 12h TU2, так що для цього моменту ТА1 = TU2. Різниці шкал TU2 - ТА1 публікуються щомісяця в бюлетені «Еталонний час». Однак прийнята в колишньому СРСР шкала часу TU2 відрізняється на декілька милiсекунд від відповідної міжнародної системи часу. Крім звичайного календарного рахунку днів, місяців і років, в астрономії широко застосовують також систему суцільного рахунку діб, яку називають юліанською системою і яка починається в середній грінвічський полудень 1 січня 4713 р. до н. е. По юліанській системі суцільного рахунку діб вирішують часто виникаючу в астрономії задачу про число діб між двома датами. Для зручності вирішення цієї задачі в «Астрономічному щорічнику» даються таблиці діб юліанського періоду, по яких можуть бути визначені юліанські дати JD, відповідні датам t по звичайному календарю. Юліанська дата застосовна як до моментів всесвітнього часу TU, так і до моментів ефемеридного часу ТЕ. Стосовно ефемеридного часу вона позначається JED. Юліанська ефемеридна дата JED відрізняється від юліанської дати JD в системі всесвітнього часу на поправку ΔТ за ефемеридний час. Для суцільного рахунку зоряних (істинних або середніх) діб застосовується поняття про юліанську зоряну дату, яка позначається JSD. Вона рівна проміжку зоряного часу, що протік від початку юліанського періоду до даного моменту і вираженому в зоряних (істинних або середніх) добах.
|













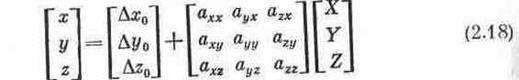




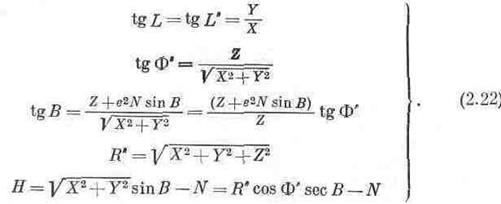

























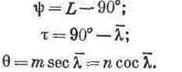



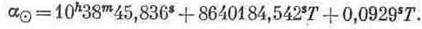

 пряме сходження середнього екваторіального сонця, що підліковується від середньої точки весняного рівнодення, а Nа, - нутація по прямому сходженню.
пряме сходження середнього екваторіального сонця, що підліковується від середньої точки весняного рівнодення, а Nа, - нутація по прямому сходженню.