 ПОЗНАВАТЕЛЬНОЕ
| Розрахунок напруженості і потенціалу
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ “КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ” Кафедра загальної і теоретичної фізики
Розрахунково-графічна робота з дисципліни “Загальна фізика” Варіант №11
Виконав: Лифар Владислав Ілліч КМ-21, ФПМ
Київ 2013
Зміст 1. Електричне поле зарядів у вакуумі 3 1.1 Напруженість електричного поля. 4 1.2 Потенціал. 6 1.3 Розрахунок напруженості і потенціалу. 8 1.4 Графіки залежності E1(r), E2(r), E3(r), φ1(r), φ2(r), φ3(r) 9 2. Електричне поле в діелектриках. Конденсатори. Енергія поля. 12 2.1 Отримати вирази для векторів електричного зміщення, напруженості та потенціалу поля у всьому просторі. 13 2.2 Розрахувати таблиці значень та побудувати графіки залежностей 2.3 Отримати вираз для ємності конденсатора та обчислити.. 19 2.4 Отримати вираз для енергії конденсатора через ємність і заряд та обчислити. 19 2.5 Отримати вираз для енергії поля конденсатора через об'ємну густину енергії; порівняти результат із попереднім розрахунком. 19 Висновки 21
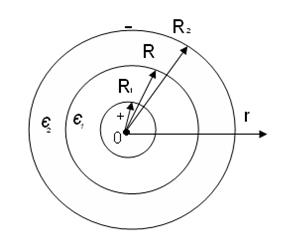
Електричне поле зарядів у вакуумі Електричне поле створюється у вакуумі (діелектрична проникність ε=1) зарядом, який розподілений із густиною ρ(r) по об'єму нескінченного циліндричного шару, r – відстань від осі. ρ(r)= ρ0(R1/r) ρ0 = 0,5 *10-6 Кл/м3 R1 = 5 см R2 = 10 см
1.1 Напруженість електричного поля
За теоремою Гаусса замкнену поверхню доводиться брати у вигляді скінченного прямого циліндра радіуса rі певної висоти h. При цьому основи циліндра не є еквіпотенціальними. Але оскільки вектор Е має радіальний напрям і складає кут 90° з нормаллю до основи, на основах нормальна проекція напруженості Еn = 0. Тому потік створюється тільки крізь бічну поверхню циліндра. Sбічна = 2πrh Маємо формулу розрахунку напруженості:
Формула для даної задачі з урахуванням значення діелектричної проникності
Формула для даної задачі з урахуванням значення діелектричної проникності
1) r < R1 Область порожняя, отже очевидно, що вільна від заряду. Тобто: q1 = 0 E1S = 0 E1= 0
2) R1≤ r ≤ R2 Оберемо тонкий циліндр радіуса r та товщини dr. Причому, dr<<r.
dV=2πrh dr
r r r q2 = ∫ ρ(r)2πrh dr = 2πh ∫ρ0(R1/r)r dr = 2πhρ0R1 ∫dr = 2πhρ0R1(r – R1) R1 R1 R1
q2 = πhρ0R1(r – R1) E2 = 2πhρ0R1(r – R1)/2πε0rh = ρ0R1(r – R1)/ε0r E2 =ρ0R1(r – R1)/ε0r
3) R2 < r q3 = Q – повний заряд шару всередині замкненого циліндру.
R2 R2 R2 q3 = ∫ ρ(r)2πrh dr = 2πh ∫ρ0(R1/r)r dr = 2πhρ0R1 ∫dr = 2πhρ0R1(R2 – R1) R1 R1 R1 E3 = 2πhρ0R1(R2 – R1)/2πε0rh = ρ0R1(R2 – R1)/ε0r
E3 = ρ0R1(R2 – R1)/ε0r Потенціал
1) R1≤ r ≤ R2
R2 R2 φ2(r) = ∫ρ0R1(r – R1)/ε0r dr = ∫(ρ0R1r/ε0r – ρ0(R1)2/ε0r)dr = r r R2 R2 = ∫ρ0R1/ε0 dr – ρ0(R1)2/ε0∫rdr = ρ0R1(R2 – r)/ε0 – ρ0(R1(R2 – r))2/2ε0 = r r = ρ0R1(R2 – r)(2 – R1(R2 – r)) /2ε0. 2) R2 < r
R2 R2 φ3(r) = ∫ρ0R1(R2 – R1)/ε0r dr = ρ0R1(R2 – R1)/ε0∫(1/r)dr = r r = ρ0R1(R2 – R1)(ln(R2) – ln(r)) / ε0. 3) r < R1 В силу визначення запишемо
Так як область порожняя, отже очевидно, що вільна від заряду, тоді E1 = 0
Отже маємо еквіпотенціальну поверхню
φ(R1) = φ1(R2) = φ2(R1)
φ1(r) = φ2(R1) Розрахунок напруженості і потенціалу
· Напруженість
E1= 0 E2= ρ0R1(r – R1)/ε0r = ρ0R1/ε0 - ρ0(R1)2/ε0r = = (0,5 *10-6 * 5 * 10-2 / 8.85 * 10-12) – (0,5 *10-6 * 25 * 10-4 / r * 8.85 * 10-12)= = E3= ρ0R1(R2 – R1)/ε0r = = 0,5 *10-6 * 5 * 10-2 * (10 – 5) * 10-2 / r * 8.85 * 10-12 = = 25, 424 * 102 / r = · Потенціал φ1(r)=φ2(R1) = 103 * (2 – 5 * 10-3 – 50 * 5 * 10-2 * 10-3)(2,5 – 25*5 * 10-2)/ 17,7 = 103 * (2 – 0,005 – 2,5)(2,5 – 1,25)/ 17,7 = φ2(r) = ρ0R1(R2 – r)(2 – R1(R2 – r)) /2ε0= (((0,5 *10-6* 5 * 10-2 * 10 * 10-2) – (0,5 *10-6* 5 * 10-2 * r)) * * = = φ3(r) = ρ0R1(R2 – R1)(ln(R2) – ln(r))/ε0 = (0,5 *10-6 * 5 * 10-2 * 5 * 10-2 )( ln10 – ln(r)) /8.85 * 10-12 = = 1412, 4( ln10 – ln(r)) (В)
1.4 Графіки залежності E1(r), E2(r), E3(r), φ1(r), φ2(r), φ3(r)
Графік залежності E1(r)
Графік залежності E2(r)
Графік залежності E3(r)
Графік залежності φ1(r)
Графік залежності φ2(r)
Графік залежності φ3(r)
2. Електричне поле в діелектриках. Конденсатори. Енергія поля.
Циліндричний конденсатор. Довжина конденсатора 10
2.1 Отримати вирази для векторів електричного зміщення Оскільки в зовнішньому електричному колі діелектрик поляризується, то розрахунок починаємо зі знаходження поля вектора електричного зміщення
Маємо: R1<r<R, 2πrhˑD=q D2= R<r<R2, 2πrhˑD=q D3= r>R2, D4=0 Оскільки діелектрик є ізотропним, то справедливо наступне співвідношення: Звідси маємо r>R2, E1=0 R<r<R2, E2 = R1<r<R, E3 = r<R1, E4=0
Так як потенціал чисельно дорівнює роботі поля по переміщенню додатного точкового заряду з даної точки на нескінченність, а робота консервативних сил в полі не залежить від форми траєкторії, тому можна записати, що
Тоді можна записати:
2.2 Розрахувати таблиці значень та побудувати графіки залежностей
D1= D4=0 (Кл/м2)
D2= D3=
E1= E4=0 (В/м)
E2=
E3=
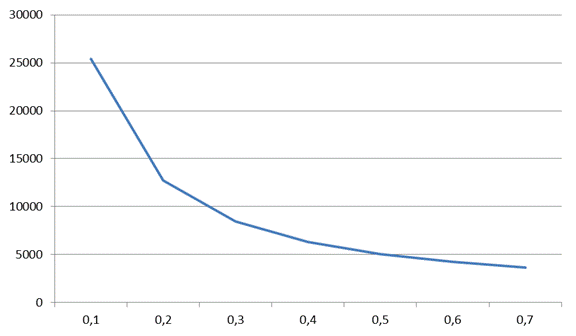
Графік залежності D(r)
Графік залежності E(r)
Графік залежності
Графік залежності ε(r)
|



 ,
, 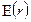 ,
,  та
та 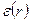 . 15
. 15
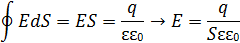






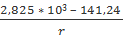 (В/м)
(В/м) (В/м)
(В/м) =-35,66 (В)
=-35,66 (В) =
= =
= (кВ)
(кВ)




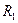
 ;
;  ;
;  ;
;  ;
;  =0.1м;
=0.1м; 




 , напруженості
, напруженості  та потенціалу
та потенціалу  . За теоремою Гаусса для вектора
. За теоремою Гаусса для вектора  , де q – алгебраїчна сума сторонніх зарядів під поверхнею.
, де q – алгебраїчна сума сторонніх зарядів під поверхнею.
 .
.


 В за умовою.
В за умовою.

 (
(  +
+  )
) =
=  (
( 

 =
= 
 (
(  +
+  )+
)+ 
 (Кл/м2)
(Кл/м2) (В/м)
(В/м)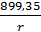 (В/м)
(В/м) (В)
(В) (В)
(В)
 (В)
(В)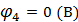
 (r), В
(r), В



 (r)
(r)