 ПОЗНАВАТЕЛЬНОЕ
| Крайова задача для лінійного диференціального рівняння другого порядку.
Числові методи розв’язання звичайних диференціальних рівнянь Задача Коші. Розглянемо найпростішу постановку задачі для рівняння першого порядку. А саме, треба знайти таку неперервну функцію
та початковій умові
де
1.1.1. Метод Ейлера. Відрізок Позначимо Замінимо в (1) похідну Одержимо для наближених значень
або
Тому що Для зменшення похибки із збереженням того ж кроку, застосовується модифікація методу – метод Ейлера з ітераціями. Нехай
Для обчислення інтеграла в правій частині (4) застосовуємо формулу трапецій. Якщо покласти
Таким чином,
Ітерації за формулами (5) виконуються доти, доки не виконається нерівність
де Після цього приймаємо
Якщо при Можна довести, що метод Ейлера є стійким, якщо Метод Ейлера застосовується також для розв’язання задачі Коші для системи диференціальних рівнянь.
В цьому випадку замість (5) будемо мати
Замість (6) одержимо
1.1.2. Методи Рунге-Кутта Ідею методу викладемо лише схематично. Постановка задачі та сама, що в 1.1. Розбиття відрізку Наближений розв’язок задачі шукається із співвідношення
де
Величини Позначимо Можна показати, що у випадку На практиці зазвичай використовують випадок
(без доведення виконнання умов методу) Якщо в наведених формулах послідовно покладати
Крайова задача для лінійного диференціального рівняння другого порядку. Крайова задача полягає в наступному. Необхідно відшукати розв’язок
що задовольняє двом крайовим умовам:
де
В загальному випадку крайова задача (11), (12) може мати або один розв’язок, або нескінченну множину розв’язків, або зовсім ні одного розв’язку. З теорії диференціальних рівнянь відомо, що для того, щоб існував єдиний розв’язок
мала тільки тривіальний розв’язок Ми спочатку будемо розглядати частинний випадок задачі (11), (12), а саме крайову задачу
де
В теорії диференціальних рівнянь доводиться, що крайова задача (15), (16) має єдиний розв’язок
1.2.1. Різницевий метод Ідея цього методу полягає в тому, що розв’язок задачі шукається не на всьому відрізку Повернемось до задачі (15), (16). Задамо на відрізку
де Множина Через Замінивши у внутрішніх вузлах сітки
Ми пере позначили u на у тому, що від похідних Неважку переконатись в тому, що система (17), (18) зводиться до системи з трьох-діагональної матрицею, причому за умови
де виконуються умови використання методу прогонки для її розв’язання (що і робиться на практиці). Можна показати, що розв’язок задачі (17), (18) збігається до розв’язку задачі (15), (16) при
де під нормою розуміється
Питання збіжності розв’язків різницевих схем до розв’язків диференціальних задач докладно вивчається в курсі «Додаткові розділи чисельного аналізу».
Розглянемо більш загальну задачу, а саме крайову задачу
де Крайова задача (15), (16*) за тих же умов до функцій Ці похідні наближено заміняються першими різницевими похідними,
Без доведення наведемо різницеву схему для крайової задачі (15), (16*):
де коефіцієнти
Можна довести, що за умови (19), виконуються властивості апроксимації, стійкості, та має місце збіжність розв’язку у різницевої схеми (20), (21) до розв’язку u диференціальної задачі (15), (16*) з порядком точності Зауважимо знову, що для розв’язку системи алгебраїчних рівнянь може бути застосований метод прогонки (можна перевірити, що умови застосування цього методу в даній ситуації виконується). |



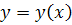 на відрізку
на відрізку  , що задовольняє диференціальному рівнянню
, що задовольняє диференціальному рівнянню (1)
(1) (2)
(2) та
та  задані.
задані. розіб’ємо на N відрізків рівної довжини
розіб’ємо на N відрізків рівної довжини  ,
,  з кроком
з кроком  , так що
, так що  .
. .
. першою різницевою похідною в точці
першою різницевою похідною в точці  .
.
 (3)
(3) відоме, (3) дає змогу послідовно відшукати всі
відоме, (3) дає змогу послідовно відшукати всі  (наближено). В цьому полягає метод Ейлера. Похибка в кожній формулі з (3) має порядок
(наближено). В цьому полягає метод Ейлера. Похибка в кожній формулі з (3) має порядок  .
. відоме, треба знайти
відоме, треба знайти . (4)
. (4) .
. , то одержимо (наближено)
, то одержимо (наближено)
 (5)
(5) , (6)
, (6) - задана точність обчислень.
- задана точність обчислень. . (7)
. (7) нерівність (6) не задовольниться, то крок h ділимо навпіл і знову обчислюємо
нерівність (6) не задовольниться, то крок h ділимо навпіл і знову обчислюємо  за формулами (5).
за формулами (5). задовольняє умову Ліпшиця по
задовольняє умову Ліпшиця по  з деякою константою
з деякою константою  .
.
 (8)
(8) (9)
(9) . (10)
. (10)

 визначаються з деяких умов.
визначаються з деяких умов. . Якщо
. Якщо  і
і  - гладкі функції параметра h. Припустимо, що
- гладкі функції параметра h. Припустимо, що 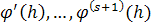 . Величини
. Величини 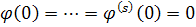 , a
, a  . Величина
. Величина  ми приходимо до методу Ейлера.
ми приходимо до методу Ейлера.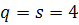 . Тут найбільш вживана сукупність формул:
. Тут найбільш вживана сукупність формул:

 , та скористатись початковими умовами
, та скористатись початковими умовами  , то можна одержати алгоритм наближеного розв’язку задачі Коші в усіх вузлах
, то можна одержати алгоритм наближеного розв’язку задачі Коші в усіх вузлах 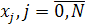 . Можна показати, що похибка розв’язку має порядок
. Можна показати, що похибка розв’язку має порядок  .
. диференціального рівняння
диференціального рівняння (11)
(11) (12)
(12) - задані функції,
- задані функції, – задані числа, такі що
– задані числа, такі що .
. (13)
(13) (14)
(14) .
. (15)
(15) (16)
(16)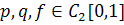 - задані функції,
- задані функції, на
на  ,
,  - задані числа.
- задані числа. .
. , а тільки в деяких його точках, на так званій сітці. Другою ідеєю методу є заміна похідних в диференціальному рівнянні (а в загальному випадку крайової задачі (11), (12) і в крайових умовах) різницевими похідними. Це дає змогу перейти від неперервної задачі до задачі розв’язку системи лінійних алгебраїчних рівнянь, яка дає наближені значення шуканої функції у вузлах сітки.
, а тільки в деяких його точках, на так званій сітці. Другою ідеєю методу є заміна похідних в диференціальному рівнянні (а в загальному випадку крайової задачі (11), (12) і в крайових умовах) різницевими похідними. Це дає змогу перейти від неперервної задачі до задачі розв’язку системи лінійних алгебраїчних рівнянь, яка дає наближені значення шуканої функції у вузлах сітки.
 натуральне.
натуральне. називається сіткою, h – кроком сітки.
називається сіткою, h – кроком сітки. позначимо підмножину
позначимо підмножину  . Множина вузлів
. Множина вузлів  - сітка, що складається з двох крайніх вузлів. Значення якої небудь функції у вузлах сітки будемо позначати
- сітка, що складається з двох крайніх вузлів. Значення якої небудь функції у вузлах сітки будемо позначати  , аналогічно
, аналогічно  .
. на другу різницеву похідну, одержуємо замість (15), (16) систему лінійних алгебраїчних рівнянь
на другу різницеву похідну, одержуємо замість (15), (16) систему лінійних алгебраїчних рівнянь , (17)
, (17)
 (18)
(18) ми перейшли до їх наближених значень і, таким чином
ми перейшли до їх наближених значень і, таким чином  не повинні задовольняти систему (17), (18), а її задовольняють деякі наближені до
не повинні задовольняти систему (17), (18), а її задовольняють деякі наближені до  , (19)
, (19) ,
, з другим порядком відносно h, тобто
з другим порядком відносно h, тобто

 , (15)
, (15) (16*)
(16*) – задані числа, причому
– задані числа, причому  .
. , що і в попередній задачі, також має єдиний розв’язок
, що і в попередній задачі, також має єдиний розв’язок 

 , (21)
, (21) вільні члени
вільні члени  визначені формулами:
визначені формулами:


