Піднесення до степеня та добування кореня.
Комплексні числа Комплексною змінною називають упорядковану пару дійсних змінних  , яку записують у вигляді , яку записують у вигляді  , ,
де  уявна одиниця, що задовольняє умові уявна одиниця, що задовольняє умові  . . Змінні  та та  називають дійсною та уявною частинами змінної називають дійсною та уявною частинами змінної 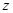 , відповідно, і позначають так: , відповідно, і позначають так: 
Зокрема,  дійсна змінна; дійсна змінна;  чисто уявна змінна; чисто уявна змінна;
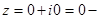 нуль. нуль.
Комплексні змінні  та та  називають рівними, якщо рівні їх дійсні та уявні частини, тобто називають рівними, якщо рівні їх дійсні та уявні частини, тобто 
На площині з декартовою системою координат х0у комплексну змінну  можна зобразити точкою М(х,у) або радіус-вектором цієї точки. Тоді між точками площини і комплексними числами встановлюється взаємно однозначна відповідність. Дійсні числа будуть зображуватись точками осі 0х, яку називають дійсною віссю, а чисто уявні числа - точками осі 0у, яку називають уявною віссю; точка можна зобразити точкою М(х,у) або радіус-вектором цієї точки. Тоді між точками площини і комплексними числами встановлюється взаємно однозначна відповідність. Дійсні числа будуть зображуватись точками осі 0х, яку називають дійсною віссю, а чисто уявні числа - точками осі 0у, яку називають уявною віссю; точка  початок координат, а площину х0у називають комплексною площиною С (Мал.1).. початок координат, а площину х0у називають комплексною площиною С (Мал.1)..  Y Y
    z=x+iy y z=x+iy y
 r r 
  x X x X
Мал.1 Позначимо через  полярний радіус і через полярний радіус і через  - полярний кут точки - полярний кут точки 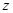 . Тоді . Тоді   
Числа  та та  називають модулем та аргументом комплексної змінної називають модулем та аргументом комплексної змінної 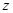 і позначають і позначають 
Модуль 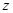 визначають однозначно за формулою визначають однозначно за формулою   
а аргумент 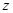 приймає нескінченну кількість значень приймає нескінченну кількість значень  які відрізняються між собою на число кратне які відрізняються між собою на число кратне  Одне значення  (позначається (позначається  що задовольняє умові що задовольняє умові  називають головним. Тоді називають головним. Тоді   
Головне значення  визначають рівностями визначають рівностями 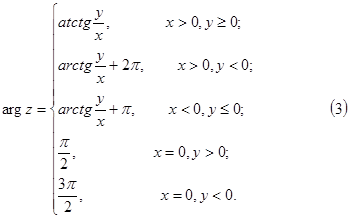
Запис комплексної змінної у вигляді   
називають алгебраїчною формою змінної  Запис вигляду    
називають тригонометричною формою змінної  Використовуючи формулу Ейлера   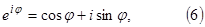
Отримаємо показникову форму змінної 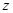    
 Означення 1. Комплексне число Означення 1. Комплексне число  називається комплексно спряжненим до числа називається комплексно спряжненим до числа  і позначається і позначається 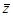 , тобто , тобто

У комплексно спряжнених чисел 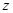 та та 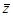 модулі рівні, аргументи відрізняються лише знаком. Числа модулі рівні, аргументи відрізняються лише знаком. Числа 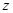 та та 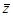 зображуються точками, які симетричні відносно дійсної осі. зображуються точками, які симетричні відносно дійсної осі.  Означення 2. Комплексне число Означення 2. Комплексне число  називається протилежним комплексним числом до числа називається протилежним комплексним числом до числа 
Якщо  то число то число  називається оберненим комплексним числом до числа називається оберненим комплексним числом до числа  2.Дії з комплексними числами. Додавання та відніманнякомплексних чисел, заданих в алгебраїчній формі  здійснюється за формулою здійснюється за формулою   
Отже, алгебраїчна сума двох комплексних чисел є комплексне число, дійсна та уявна частина якого дорівнює тій самій алгебраїчній сумі дійсних та уявних частин, відповідно. Добуткомкомплексних чисел, заданих в алгебраїчній формі, називається комплексне число    (10) (10)

яке одержують за правилом множення многочленів з урахуванням, що  Діленнякомплексних чисел визначається як дія, обернена множенню. При діленні комплексних чисел в алгебраїчній формі достатньо помножити чисельник і знаменник на число, комплексно спряжнене до знаменника, а потім відокремити дійсну та уявну частини:      
  Якщо комплексні числа Якщо комплексні числа  та та  задані в тригонометричній формі, то їх добуток знаходиться за формулою: задані в тригонометричній формі, то їх добуток знаходиться за формулою:
 
Дійсно  
 . .
При множенні комплексних чисел їх модулі перемножуються, а аргументи додаються т.т.  
Аналогічно доводиться, що при діленні комплексних чисел \їх модулі діляться, а аргументи додаються: 
   (13) (13)
   Якщо комплексні числа задані у показниковій формі, то Якщо комплексні числа задані у показниковій формі, то
 
 (15) (15)
З (12) та (13) випливає, що при множенні комплексного числа  на на  вектор вектор  розтягується в розтягується в  раз і повертається на кут раз і повертається на кут  проти руху годинникової стрілки. проти руху годинникової стрілки.   y y 


   x x
 Мал.2 Мал.2
Зокрема, множення 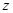 на на  зводиться до повороту вектора зводиться до повороту вектора 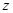 на кут на кут  без розтягування. З формул (13) та (15) випливає, що при діленні комплексних чисел їх модулі діляться, а аргументи віднімаються. без розтягування. З формул (13) та (15) випливає, що при діленні комплексних чисел їх модулі діляться, а аргументи віднімаються.  Приклад 1. Знайти алгебраїчну форму суми Приклад 1. Знайти алгебраїчну форму суми

 Розв’язання.Оскільки Розв’язання.Оскільки
 то то
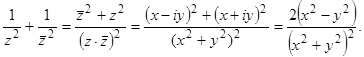
Піднесення до степеня та добування кореня. Правило множення комплексних чисел поширюється на довільну кількість множників. Зокрема, якщо усі множники дорівнюють  то то


Цю формулу називають формулою Мавра, з неї отримуємо  Знайти корінь цілого додатного степеня  з числа з числа  означає, що треба знайти таке число означає, що треба знайти таке число   я степінь якого дорівнює я степінь якого дорівнює  Тому за формулою (13) маємо: Тому за формулою (13) маємо:

З першої цих рівностей знаходимо  а з другої а з другої  Знаходження кореня  степеня із комплексного числа степеня із комплексного числа  здійснюють за формулою: здійснюють за формулою:   
З цієї формули випливає, що є  різних значень різних значень  . Кожному із цих . Кожному із цих  значень відповідає точка комплексної площини. Усі ці точки лежать на колі радіуса значень відповідає точка комплексної площини. Усі ці точки лежать на колі радіуса  з центром в початку координат і поділяють коло на з центром в початку координат і поділяють коло на  рівних частин. рівних частин. Відзначимо, що у випадку задання комплексного числа 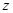 у показниковій формі у показниковій формі 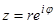 маємо: маємо:     (18) (18)
| 



 , яку записують у вигляді
, яку записують у вигляді ,
, уявна одиниця, що задовольняє умові
уявна одиниця, що задовольняє умові  .
. та
та  називають дійсною та уявною частинами змінної
називають дійсною та уявною частинами змінної 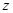 , відповідно, і позначають так:
, відповідно, і позначають так:
 дійсна змінна;
дійсна змінна; чисто уявна змінна;
чисто уявна змінна;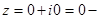 нуль.
нуль. та
та  називають рівними, якщо рівні їх дійсні та уявні частини, тобто
називають рівними, якщо рівні їх дійсні та уявні частини, тобто
 початок координат, а площину х0у називають комплексною площиною С (Мал.1)..
початок координат, а площину х0у називають комплексною площиною С (Мал.1).. Y
Y


 z=x+iy y
z=x+iy y r
r 

 полярний радіус і через
полярний радіус і через 




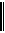


 які відрізняються між собою на число кратне
які відрізняються між собою на число кратне 
 (позначається
(позначається  що задовольняє умові
що задовольняє умові  називають головним. Тоді
називають головним. Тоді



 визначають рівностями
визначають рівностями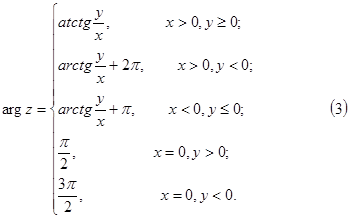










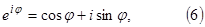



 Означення 1. Комплексне число
Означення 1. Комплексне число  називається комплексно спряжненим до числа
називається комплексно спряжненим до числа  і позначається
і позначається 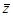 , тобто
, тобто
 Означення 2. Комплексне число
Означення 2. Комплексне число  називається протилежним комплексним числом до числа
називається протилежним комплексним числом до числа 
 то число
то число  називається оберненим комплексним числом до числа
називається оберненим комплексним числом до числа  здійснюється за формулою
здійснюється за формулою

 (10)
(10)







 та
та  задані в тригонометричній формі, то їх добуток знаходиться за формулою:
задані в тригонометричній формі, то їх добуток знаходиться за формулою:



 .
.




 (13)
(13)


 Якщо комплексні числа задані у показниковій формі, то
Якщо комплексні числа задані у показниковій формі, то

 (15)
(15) раз і повертається на кут
раз і повертається на кут  проти руху годинникової стрілки.
проти руху годинникової стрілки.
 y
y 



 без розтягування. З формул (13) та (15) випливає, що при діленні комплексних чисел їх модулі діляться, а аргументи віднімаються.
без розтягування. З формул (13) та (15) випливає, що при діленні комплексних чисел їх модулі діляться, а аргументи віднімаються. Приклад 1. Знайти алгебраїчну форму суми
Приклад 1. Знайти алгебраїчну форму суми
 Розв’язання.Оскільки
Розв’язання.Оскільки то
то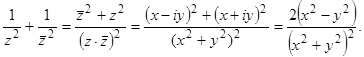
 то
то




 з числа
з числа  означає, що треба знайти таке число
означає, що треба знайти таке число
 я степінь якого дорівнює
я степінь якого дорівнює 
 а з другої
а з другої 
 здійснюють за формулою:
здійснюють за формулою:



 . Кожному із цих
. Кожному із цих  з центром в початку координат і поділяють коло на
з центром в початку координат і поділяють коло на 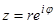 маємо:
маємо:
 (18)
(18)