 ПОЗНАВАТЕЛЬНОЕ
| Наблюдение эффектов размножения и наложения спектров. 12
Исходные данные: Х1=2, Х2=0.8, Х3=0.8, ϕ1=0, ϕ2= π, ϕ3=0, F1=1МГц, Fд=8МГц, ∆t=1/512 мкс. Требуется: 1.Определить амплитудный спектр аналогового сигнала где 2.Определить амплитудный спектр дискретного сигнала в интервале частот от 0 до 2FД+3F1, где FД – частота дискретизации. 3.Выполнить моделирование аналогового сигнала, его дискретизации и восстановления аналогового сигнала из дискретного при двух значениях частоты дискретизации: первое значение FД= 8 МГц, второе значение в два раза меньше первого FД= 4 МГц. Моделирование выполняется по программе «Diskret». 4.Сравнить аналоговый сигнал, восстановленный из дискретного, с исходным аналоговым сигналом на входе дискретизатора. Сравнение выполнить при двух значениях частоты дискретизации.
Расчет частот спектральных составляющих дискретного сигнала по формуле:
k = 0 1. F=F1, f1 = F1 = 1 МГц, 2. F=2F1, f2 = 2F1 = 2 МГц, 3. F=3F1, f3 = 3F1 = 3 МГц.
k=1 4. F=3F1, f4 = FД – 3F1 = 8 – 3 = 5 МГц, 5. F=2F1, f5 = FД – 2F1 = 8 – 2 = 6 МГц, 6. F=F1, f6 = FД – F1 = 8 – 1 = 7 МГц, 7. F=F1, f7 = FД + F1 = 8 + 1 = 9 МГц, 8. F=2F1, f8 = FД + 2F1 = 8 + 2 = 10 МГц, 9. F=3F1, f9 = FД + 3F1 = 8 + 3 = 11 МГц.
k=2 10. F=3F1, f10 = 2FД – 3F1 = 16 – 3 = 13 МГц, 11. F=2F1, f11 = 2FД – 2F1 = 16 – 2 = 14 МГц, 12. F=F1, f12 = 2FД – F1 = 16 – 1 = 15 МГц, 13. F=F1, f13 = 2FД + F1 = 16 + 1 = 17 МГц, 14. F=2F1, f14 = 2FД + 2F1 = 16 + 2 = 18 МГц, 15. F=3F1, f15 = 2FД + 3F1 = 16 + 3 = 19 МГц.
Построение спектральных диаграмм аналогового и дискретного сигналов.
Рисунок 1 – Амплитудный спектр аналогового сигнала
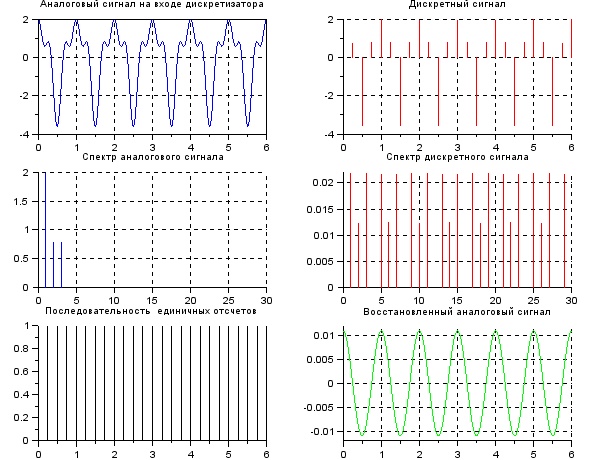
Рисунок 2 – Амплитудный спектр дискретного сигнала Результат моделирования по программе «Diskret A» в виде временных и спектральных диаграмм аналогового и дискретного сигнала приведён на рисунке 3.
Рисунок 3. Временные и спектральные диаграммы при FД > 2F3 Вывод: При увеличении дискретизации возникает эффект размножения спектра и восстановленный аналоговый сигнал совпадает по форме с исходным, так как соблюдается теорема Котельникова.
Повторим эксперимент при уменьшенной в два раза частоты дискретизации.
Рисунок 4. Временные и спектральные диаграммы при FД < 2F3 Вывод: При уменьшении дискретизации в 2 раза, восстановленный и исходный сигнал не совпадает по форме, так как не соблюдается теорема Котельникова и происходит эффект наложения. Задание №1б.Моделирование процесса дискретизации аналогового сигнала, модулированного по амплитуде, и восстановления аналогового сигнала из дискретного.
Исходные данные: X0=2, f0=13, F=0.20, FД=4, Δt=1/256 Задание 1б выполняется по программе «Diskret_B» (Приложение Б). Эта программа отличается от программы «Diskret_A» только видом функции, описывающей исходный аналоговый сигнал. Результатом выполнения программы являются временные и спектральные диаграммы аналогового и дискретного сигналов (рисунок 5).
Рисунок 5 – Временные и спектральные диаграммы аналогового и дискретного сигналов при частоте несущей f0=13 МГц, частоте модуляции 0.20 МГц и частоте дискретизации FД=4МГц Вывод: восстановленный аналоговый сигнал идентичен сигналу на входе дискретизатора. Задание №2.Определение спектра восьмиточечной последовательности отсчетов сигнала с использованием алгоритмов БПФ с прореживанием во времени и с прореживанием по частоте и выполнение обратного преобразования.
2.1. Определение спектра последовательности xn, где n = 0,1,2..7, методом прямого дискретного преобразования Фурье
где 2.2. Определение последовательности отсчетов сигнала xn, где n = 0,1,2..7, по известной последовательности отсчетов спектра Sk, где k = 0,1,2..7, методом обратного дискретного преобразова- ния Фурье
где n = 0,1,2..7.
2.3. Определение спектра последовательности xn, где n = 0,1,2..7, методом БПФ с прореживанием во времени. 2.4. Определение последовательности отсчетов сигнала xn, где n=0,1,2..7, по известной последовательности отсчетов спектра Sk, где k=0,1,2..7, методом БПФ с прореживанием во времени. 2.5. Определение спектра последовательности xn, где n = 0,1,2..7, методом БПФ с прореживанием по частоте. 2.6. Определение последовательности отсчетов сигнала xn, где n=0,1,2..7, по известной последовательности отсчетов спектра Sk, где k=0,1,2..7, методом БПФ с прореживанием по частоте.
Определим спектр заданной последовательности по программе «Прямое ДПФ»:
Спектр амплитуд:
Спектр фаз:
Спектры амплитуд и фаз приведены на рисунках 2.1 и 2.2 соответственно.
Рисунок 2.1 – Спектр амплитуд.
Рисунок 2.2 – Спектр фаз.
2. Определим последовательность отсчетов дискретного сигнала по её спектру.
Воспользовавшись программой «Обратное ДПФ», получим:
3. Воспользуемся алгоритмом прямого БПФ с прореживанием во времени для исходной последовательности.
Рисунок 2.3
Выполним перестановку членов этой последовательности с учетом двоичной инверсии индексов (рисунок 2.3). В результате получим:
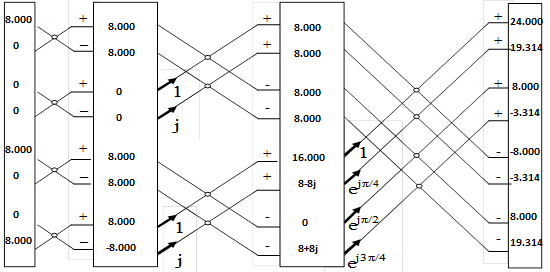
Воспользовавшись алгоритмом прямого БПФ с прореживанием во времени (рисунок 2.4), выполним операции «бабочка»: на первом уровне – 4 двухточечных «бабочки», на втором уровне – 2 четырёхточечных, на третьем уровне – одна восьмиточечная.
Рисунок 2.4 – Алгоритм прямого БПФ с прореживанием во времени.
4. Выполним перестановку членов полученной последовательности отсчетов спектра с учетом двоичной инверсии индексов. В результате получим:
Подадим эту последовательность на входы двухточечных бабочек рисунка 2.5 и выполним вычисления.
Примечание: результаты выполнения бабочки делятся на N=8
Рисунок 2.5 – Алгоритм обратного БПФ с прореживанием во времени.
5. Воспользуемся алгоритмом БПФ с прореживанием по частоте для определения прямого преобразования последовательности.
Согласно алгоритму прямого БПФ с прореживанием по частоте (рисунок 2.6), выполним операции «бабочка»: на первом уровне – одна восьмиточечная «бабочка», на втором уровне – 2 четырёхточечных, на третьем уровне – четыре двухточечных.
Рисунок 2.6 – Алгоритм прямого БПФ с прореживанием по частоте.
Выполним перестановку членов полученной последовательности с учетом двоичной инверсии индексов (рисунок 2.3). В результате получим:
6. По алгоритму рисунка 2.7 выполним обратное преобразование последовательности отсчетов спектра.
Примечание: результаты на выходах двухточечных бабочек делятся на N=8 Рисунок 2.7 – Алгоритм обратного БПФ с прореживанием по частоте. Результатом этой операции является последовательность отсчетов дискретного сигнала .
Выполнив перестановку членов этой последовательности с учетом двоичной инверсии индексов, получим.
12 |










 , N=8, k=0,1,2..7.
, N=8, k=0,1,2..7.
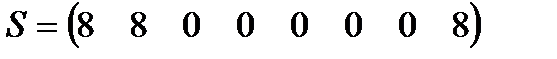 ,
,
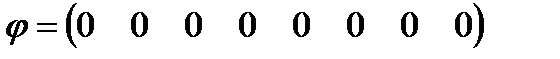


 .
.
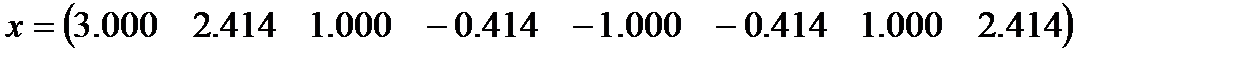






 .
.

