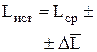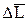ПОЗНАВАТЕЛЬНОЕ
| ИЗМЕРИТЕЛЬНЫЕ ИНСТРУМЕНТЫ.
Муромский институт (филиал) федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Владимирский государственный университет Имени Александра Григорьевича и Николая Григорьевича Столетовых»
Кафедра: «ФПМ» Дисциплина: Физика
ЛАБОРАТОРНАЯ РАБОТА № 5.01
ИЗМЕРИТЕЛЬНЫЕ ИНСТРУМЕНТЫ
Утверждена на методическом семинаре кафедры ФПМ
Зав.кафедрой _____________
ЛАБОРАТОРНАЯ РАБОТА № 5.01
ИЗМЕРИТЕЛЬНЫЕ ИНСТРУМЕНТЫ.
Приборы и принадлежности: 1. штангенциркуль, 2. микрометр, 3. микроскоп, 4. весы, 5. измеряемые предметы.
Наиболее часто встречающиеся в лаборатории измерительные приборы – это приборы для измерения линейных величин. Простейшие из них – штангенциркуль, микрометр, микроскоп, масштабная линейка. Измерение длины в простейшем случае можно произвести масштабной линейкой. Величина наименьшего деления такой линейки называется ценой одного деления. Обычно цена одного деления линейки 1 мм. Если измерения длины производят с помощью вспомогательной шкалы измерительного инструмента (нониуса), то отсчет можно произвести, с точностью до долей миллиметра. Нониус бывает линейный – для измерения линейных величин и угловой – для измерения угловых величин. Линейный нониус представляет собой небольшую линейку С со шкалой, m делений которой равны m – 1 делениям шкалы масштабной линейки А. Если d – цена деления нониуса, m – число делений на нониусе, b – цена деления масштабной линейки (рис. 1), то имеем: dm = (m – 1)b (1) Из формулы (1) получаем разность
которая называется точностью нониуса, т. е. точность нониуса равна отношению цены наименьшего деления масштаба к числу делений на нониусе. Точность нониуса частобывает равна 1/10мм; в этом случае b = 1мм, m = 10.
Измерение при помощи нониуса производят следующим образом: к нулевому делению шкалы линейки прикладывают один конец измеряемого тела В, к другому концу тела – нониус С (рис. 2). Из рис. 2 видно, что искомая длина тела В равна L = kb ± DL, (2) где k – число целых делений масштабной линейки в мм, укладывающееся в измеряемой длине, DL – отрезок длины, представляющий доли миллиметра.
Обозначим через n, то деление нониуса, которое совпадает с любым каким-то делением масштабной линейки, тогда
Из формул (2) и (3) находим искомую длину
Если положить b = 1 мм, m = 10 делений (что обычно и бывает), то искомая длина
Таким образом, длина измеряемого тела равна целому числу k мм масштабной линейки плюс десятые доли числа n. Число n показывает тот номер деления нониуса, который совпадает с некоторым делением масштабной линейки. На линейке (рис.2) приведен отсчет длины:
Линейный нониус используется в инструменте, который называется штангенциркуль. Штангенциркуль (рис.3) состоит из стальной миллиметровой линейки А, с одной стороны которой имеется неподвижная ножка Д. Вторая ножка В имеет нониус С и может перемещаться вдоль линейки А.
Когда ножки В и Д соприкасаются, нуль нониуса должен совпадать с нулем на миллиметровой линейке. Для того чтобы измерить длину предмета М, его помещают между ножками, которые сдвигают до полного соприкосновения с предметом и закрепляют винтом Е. После этого делают отсчет по линейке и нониусу и вычисляют длину предмета М по формуле (4). Значение коэффициента b для числа измерений, равного пяти (М = 5) равно 0,62. Микрометрический винт применяется в точных измерительных приборах (микрометр, микроскоп) и позволяет производить измерения до сотых долей миллиметра. Микрометрический винт представляет собой стержень, снабженный точной винтовой нарезкой. Высота подъема винтовой нарезки за один оборот называется шагом микрометрического винта. Микрометр (рис. 4 и 5) состоит из двух основных частей: скобы В и микрометрического винта А. Микрометрический вит А проходит через отверстие скобы В с внутренней резьбой. Против микрометрического винта на скобе имеется упор Е. На микрометрическом винте закреплен полный цилиндр (барабан) С с делениями по окружности. 11ри вращении микрометрического винта барабан скользит по линейной шкале, нанесенной на стебле Д.
Наиболее распространен микрометр, у которого цена делений линейной шкалы стебля b = 0,5мм. Верхние и нижние риски шкалы сдвинуты относительно друг друга на полмиллиметра, цифры проставлены только для делений нижней шкалы, т.е. нижняя шкала представляет собой обычную миллиметровую шкалу (рис. 5). Для того чтобы микрометрический винт А передвинулся на 1 мм, необходимо сделать два оборота барабана С. Таким образом, шаг микрометрического винта равен 0,5 мм. У такого микрометра на барабане С имеется шкала, содержащая 50 делений. Так как шаг винта b = 0,5мм, а число делений барабана m = 50, то точность микрометра
Для измерения микрометром предмет помещают между упором Е и микрометрическим винтом А, вращают винт А за головку М до тех пор, пока измеряемый предмет не будет зажат между упором Е и концом винта А (вращение винта А производится только за головку М, так как в противном случае легко сбить совпадение нулей шкалы и стебля и барабана). Числовое значение L измеряемого предмета находят по формуле:
где k – число наименьших делений шкалы, b – цена наименьшего деления шкалы, m – число всех делений на шкале барабана, n – номер того деления барабана, который в момент отсчета совпадает с осью шкалы стебля Д. Так как в данной работе применяется микрометр, у которого b = 0.5мм, m = 50, то формула (5) примет вид:
На рисунке 5 отсчет по микрометру показывает:
Измерение штангенциркулем и обработка результатов измерений. Штангенциркулем измеряют высоту b и диаметрd цилиндра. Измерения производят следующим образом: 1) Цилиндр помещают между ножками Д и В штангенциркуля (слегка зажав ножки) и закрепляют винт Е. 2) Измеряют длину и диаметр цилиндра и производят отсчет по шкале линейки А числа целых миллиметров k, расположенных слева от нулевого деления нониуса, и числа делений n шкалы нониуса, совпадающего с любым делением шкалы А. Но формуле (4) делают недочет. 3) Вычисляют погрешность измерений методом Стьюдента (см. лаб. раб. № 1). Результаты измерений и вычислений занести в таблицу.
Измерение микрометром и обработка результатов измерений. 1) Измеряемый предмет помещают между упором Е и концом винта А. 2) Находят значения k и n по шкале стебля Д и барабана С. По формуле (6) производят подсчет искомых величин. 3) Измерения диаметра и толщины предметов повторяют не менее пяти раз в разных местах. 4) Погрешности вычисляют, пользуясь методом Стьюдента. Результаты измерений и вычислений заносят в таблицу.
(по Стьюденту ) (по Стьюденту) |



 ,
,

 . (3)
. (3) .
. мм. (4)
мм. (4) мм = 14,5 мм, так как k = 14 мм, n = 5.
мм = 14,5 мм, так как k = 14 мм, n = 5.


 мм.
мм. , (5)
, (5) мм. (6)
мм. (6) .
.