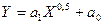ПОЗНАВАТЕЛЬНОЕ  Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д. Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Приклад розв’язування задачі
ЛАБОРАТОРНА РОБОТА №8 Тема: Парна нелінійна регресія. Мета роботи: Навчитися будувати та обчислювати параметри нелінійної регресії 1 МНК засобами MS Excel. Приклад розв’язування задачі На основі статистичних даних факторів Y та Х, знайти оцінки коефіцієнтів регресії, в припущенні, що стохастична залежність між факторами Y та Х має вигляд: 
та за критерієм Фішера на рівні значимості 0,95 оцінити адекватність одержаної моделі статистичним даним. На основі критерію Стьюдента оцінити значущість коефіцієнтів а1 та а0. Якщо отримана модель відповідає статистичним даним, то знайти прогнозне значення (точковий та інтервальний прогнози), значення коефіцієнту еластичності. На основі отриманої моделі зробити висновки. Вихідні дані та перетворення наведені в таблиці 8.1. Побудувати графіки вихідних даних, точкового та інтервального прогнозів для точки при n=11. Таблиця 8.1. Вихідні дані та перетворення | i | Xі | Yі | X1і | Ypі | | | | | | | 2,39 | 1,22 | 1,545962 | 1,584010 | | 16,83 | 4,36 | 4,102438 | 4,272927 | | 13,44 | 3,82 | 3,666061 | 3,813942 | | 8,56 | 3,61 | 2,925748 | 3,035277 | | 12,81 | 3,52 | 3,579106 | 3,722483 | | 19,45 | 4,56 | 4,410215 | 4,596649 | | 26,82 | 5,25 | 5,178803 | 5,405054 | | 18,45 | 4,42 | 4,295346 | 4,475829 | | 12,52 | 4,05 | 3,538361 | 3,679627 | | 15,39 | 3,86 | 3,923009 | 4,084202 | | Прогноз | 24,05 | | 4,904080 | 5,116099 | Розв’язування. Зведемо дану функцію до лінійної. Для цього виконаємо перетворення:  . Результати запишемо у стовпець 4. У підсумку отримаємо звичайну лінійну регресію: . Результати запишемо у стовпець 4. У підсумку отримаємо звичайну лінійну регресію: 
Далі застосуємо регресійний аналіз (функція ЛИНЕЙН) до наступних змінних: Х1 та Y. Отримаємо наступні параметри лінійної регресії: | а1 | 1,0518 | -0,0420 | а0 | | Sа1 | 0,1032 | 0,3952 | Sа0 | | R2 | 0,9285 | 0,3015 | E | | F | 103,8614 | | n-k | | S2рег | 9,4432 | 0,7274 | S2зал | Тобто, в результаті обчислень, ми отримали наступну економетричну модель:  . .
Перевіримо її на достовірність. Для цього, порівняємо одержане значення критерію Фішера з табличним на рівні значимості 0,95 та степенях свободи m1=1 та m2=8: Fтаб=5,3177. Так як F > Fтаб, то отримана модель достовірна з ймовірністю 0,95. Оскільки R2=0,9285, то це значить, що 92,85% вихідних даних відповідають отриманій регресії, а коефіцієнт кореляції R=0,9636. Це говорить про тісний зв’язок між факторами Х та Y. Перевіримо на достовірність коефіцієнти моделі. для цього обчислимо критерії Стьюдента для кожного з них та порівняємо їх з табличним значенням критерію Стьюдента на рівні значимості 0,95 та числу степенів свободи n-k=8. tтаб=2,3060; t(a1)=10,191; t(a0)=0,1064. Так як  , то коефіцієнт а1 достовірний з ймовірністю 0,95. , то коефіцієнт а1 достовірний з ймовірністю 0,95. Так як  , то коефіцієнт а0 статистично не відрізняється від нуля. , то коефіцієнт а0 статистично не відрізняється від нуля. Знайдемо прогнозне значення фактора Y в прогнозній точці, тобто в точці Х=24,05. Оскільки ми специфікували регресію функцією  , то наша прогнозна точка буде Х1=4,904. У таблиці 8.1 у стовпці 5 наведені розрахункові (теоретичне) значення отриманої регресії. Ми бачимо, що прогнозне значення Y=5,116. , то наша прогнозна точка буде Х1=4,904. У таблиці 8.1 у стовпці 5 наведені розрахункові (теоретичне) значення отриманої регресії. Ми бачимо, що прогнозне значення Y=5,116. Обчислимо 95% надійний інтервал для прогнозного значення (інтервальний прогноз). Методика обчислення була дана в лабораторній роботі №6, а тому приводимо лише значення: Ymin=4,334; Ymax=5,898 Коефіцієнт еластичності k=0,505 Висновки: 1. Оскільки  , то отримана нами економетрична модель , то отримана нами економетрична модель  достовірна з ймовірністю 0,95. Так як R2=0,9285, то 92,85% вихідних даних підпорядковуються обраній регресії достовірна з ймовірністю 0,95. Так як R2=0,9285, то 92,85% вихідних даних підпорядковуються обраній регресії  . . 2. Коефіцієнт а1 достовірний з ймовірністю 0,95, оскільки  ; коефіцієнт а0 статистично дорівнює 0, так як ; коефіцієнт а0 статистично дорівнює 0, так як  . Так як а1=1,0518, то це значить, що при збільшенні фактора Х на 1 у.о. фактор Y збільшиться на 1,0518 у.о. . Так як а1=1,0518, то це значить, що при збільшенні фактора Х на 1 у.о. фактор Y збільшиться на 1,0518 у.о. 3. Прогнозне значення фактора Y буде дорівнювати Yпр=5,116. З ймовірністю 0,95 воно буде знаходитися в межах від 4,434 до 5,898. 4. Коефіцієнт еластичності k=0,505 показує, що при зміні фактора Х на 1% фактор Y в середньому буде змінюватися на 0,505%. 5. Так як отримана модель однофакторна, то можна побудувати графік залежності між факторами Х та Y, а також на цьому ж графіку показати розрахункові точки отриманої регресії. 
Варіанти для самостійної роботи (вхідні бази даних фактора Х та Y) Завдання 1.Вивчіть розв’язок прикладу лабораторної роботи. 2.На основі статистичних даних факторів Х та Y знайдіть оцінки параметрів лінії регресії, якщо функція задана у вигляді  . . За критерієм Фішера на рівні значимості 0,95 оцінити адекватність прийнятої моделі статистичним даним. Якщо модель достовірна, то: - оцінити значущість коефіцієнтів моделі; - знайти коефіцієнт кореляції; - точковий та інтервальний прогнози; - коефіцієнт еластичності; - зробити висновки; - побудувати графіки експериментальних та теоретичних даних, точкового та інтервального прогнозів.
Таблиця 8.2. Форма стохастичної залежності та вихідні дані | № п/п | Варіант № 1 | Варіант № 2 | Варіант № 3 | Варіант № 4 | Варіант № 5 | Варіант № 6 | Варіант № 7 | Варіант № 8 |  |  |  |  |  |  |  |  | | 1,01 | 12,03 | 1,02 | 3,02 | 1,08 | 4,37 | 1,08 | 1,84 | 1,10 | 2,72 | 5,12 | 6,50 | 9,35 | 8,68 | 1,15 | 5,44 | | 1,51 | 8,84 | 1,59 | 2,94 | 1,53 | 4,01 | 1,55 | 2,22 | 1,33 | 2,91 | 10.59 | 7,17 | 15,26 | 9,86 | 1,64 | 7,01 | | 2,02 | 6,99 | 2,12 | 2,71 | 2,05 | 3,29 | 2,09 | 3,54 | 1,58 | 3,18 | 15,07 | 7,39 | 20,67 | 10,65 | 2,28 | 10,62 | | 2,51 | 6,03 | 2,61 | 3,32 | 2,58 | 3,10 | 2,52 | 3,50 | 1,81 | 3,50 | 21,42 | 7,85 | 26,49 | 11,20 | 2,77 | 13,40 | | 3,01 | 5,55 | 3,05 | 2,69 | 3,02 | 3,22 | 3,07 | 5,30 | 2,09 | 3,71 | 27,33 | 8,01 | 33,14 | 11,87 | 3,42 | 17,42 | | 3,49 | 5,12 | 3,56 | 2,99 | 3,58 | 2,99 | 3,57 | 5,42 | 2,32 | 3,88 | 32,76 | 8,20 | 39,39 | 12,32 | 3,78 | 21,70 | | 3,98 | 4,63 | 4,00 | 3,22 | 4,06 | 2,90 | 4,05 | 7,12 | 2,59 | 4,06 | 37,07 | 8,23 | 44,49 | 12,59 | 4,49 | 28,60 | | 4,48 | 4,41 | 4,50 | 3,42 | 4,56 | 2,37 | 4,56 | 8,27 | 2,85 | 4,18 | 45,20 | 8,49 | 50,71 | 12,85 | 5,08 | 35,68 | | 4,99 | 4,01 | 5,03 | 4,00 | 5,01 | 1,87 | 5,06 | 8,71 | 3,14 | 4,39 | 49,34 | 8,57 | 56,01 | 13,18 | 5,63 | 41,37 | | 5,49 | 3,96 | 5,56 | 3,43 | 5,51 | 1,82 | 5,53 | 10,09 | 3,43 | 4,44 | 55,13 | 8,53 | 63,00 | 13,40 | 6,11 | 49,45 | | 5,97 | 3,70 | 6,04 | 4,49 | 6,06 | 1,89 | 6,06 | 11,30 | 3,69 | 4,55 | 60,33 | 8,65 | 68,79 | 13,71 | 6,79 | 60,03 | | 6,47 | 3,75 | 6,50 | 4,44 | 6,52 | 2,28 | 6,50 | 12,39 | 3,90 | 4,63 | 67,24 | 8,67 | 74,97 | 13,91 | 7,39 | 68,97 | | 6,98 | 3,72 | 7,01 | 4,83 | 7,02 | 1,46 | 7,01 | 13,16 | 4,20 | 4,61 | 75,37 | 8,84 | 81,39 | 14,11 | 7,84 | 76,80 | | 7,51 | 3,53 | 7,58 | 4,62 | 7,54 | 1,56 | 7,58 | 14,67 | 4,42 | 4,66 | 82,15 | 8,83 | 87,91 | 14,20 | 8,48 | 89,84 | | 7,99 | 3,25 | 8,04 | 5,01 | 8,05 | 1,73 | 8,05 | 15,50 | 4,72 | 4,66 | 89,20 | 9,01 | 93,94 | 14,38 | 8,57 | 92,49 | | пр | 8,45 | | 8,52 | | 8,48 | | 8,52 | | 4,99 | | 94,36 | | 96,15 | | 9,46 | |
Таблиця 8.2. Форма стохастичної залежності та вихідні дані | № п/п | Варіант № 9 | Варіант № 10 | Варіант № 11 | Варіант № 12 | Варіант № 13 | Варіант № 14 | Варіант № 15 | Варіант № 16 |  |   |  |  |  |  |  | 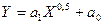 | | 0,21 | 0,19 | 0,32 | 2,44 | 0,32 | 5,71 | 1,03 | 1,27 | 0,38 | 8,33 | 0,11 | 1,78 | 1,01 | 5,02 | 9,33 | 9,67 | | 0,69 | 0,47 | 0,93 | 3,62 | 0,93 | 5,97 | 1,63 | 1,42 | 0,93 | 7,97 | 0,39 | 2,22 | 1,35 | 5,51 | 15,72 | 11,82 | | 1,03 | 0,67 | 1,59 | 4,98 | 1,48 | 3,82 | 2,16 | 1,93 | 1,61 | 4,60 | 0,66 | 4,30 | 1,74 | 6,52 | 20,87 | 13,76 | | 1,38 | 0,66 | 2,29 | 5,43 | 2,16 | 3,27 | 2,71 | 2,35 | 2,35 | 4,02 | 0,89 | 5,49 | 2,09 | 7,92 | 26,74 | 13,48 | | 1,71 | 0,92 | 2,92 | 5,59 | 2,79 | 3,06 | 3,26 | 2,73 | 3,02 | 3,75 | 1,15 | 6,57 | 2,49 | 9,64 | 31,95 | 14,99 | | 2,07 | 1,00 | 3,62 | 5,94 | 3,42 | 2,86 | 3,77 | 3,93 | 3,63 | 3,72 | 1,43 | 7,15 | 2,85 | 10,06 | 37,97 | 16,74 | | 2,47 | 1,15 | 4,12 | 6,67 | 4,65 | 2,79 | 4,35 | 5,12 | 4,35 | 3,33 | 1,67 | 10,48 | 3,28 | 14,06 | 44,61 | 16,41 | | 2,92 | 1,39 | 4,42 | 9,62 | 4,99 | 2,63 | 4,91 | 6,55 | 5,02 | 3,27 | 1,95 | 12,52 | 3,64 | 19,67 | 51,32 | 17,88 | | 3,38 | 1,48 | 5,25 | 11,39 | 5,63 | 2,54 | 5,50 | 9,05 | 5,72 | 2,67 | 2,23 | 17,53 | 4,04 | 25,58 | 58,27 | 19,88 | | 3,87 | 1,72 | 6,25 | 12,60 | 6,25 | 2,60 | 6,01 | 12,24 | 6,26 | 3,26 | 2,45 | 24,23 | 4,47 | 32,56 | 64,53 | 20,50 | | 4,23 | 1,85 | 6,90 | 13,99 | 6,88 | 2,41 | 6,60 | 17,28 | 6,99 | 2,55 | 2,72 | 36,96 | 4,83 | 37,02 | 7,32 | 20,01 | | 4,64 | 1,94 | 7,56 | 17,82 | 7,81 | 2,47 | 7,20 | 25,25 | 7,59 | 2,89 | 2,93 | 41,65 | 5,20 | 47,97 | 77,53 | 22,26 | | 5,00 | 2,11 | 8,21 | 21,32 | 8,46 | 2,41 | 7,78 | 38,19 | 8,30 | 2,44 | 3,13 | 52,00 | 5,70 | 61,09 | 84,35 | 22,31 | | 5,50 | 2,32 | 8,91 | 25,76 | 8,97 | 2,50 | 8,35 | 52,81 | 9,00 | 2,92 | 3,41 | 73,81 | 6,02 | 70,61 | 90,87 | 23,34 | | 5,98 | 2,45 | 9,57 | 30,26 | 9,75 | 2,45 | 8,90 | 76,20 | 9,64 | 2,89 | 3,63 | 95,47 | 6,52 | 88,60 | 96,33 | 22,68 | | пр | 6,32 | | 10,20 | | 10,30 | | 9,42 | | 10,20 | | 3,85 | | 6,90 | | 102,68 | |
|





 . Результати запишемо у стовпець 4. У підсумку отримаємо звичайну лінійну регресію:
. Результати запишемо у стовпець 4. У підсумку отримаємо звичайну лінійну регресію:
 .
. , то коефіцієнт а1 достовірний з ймовірністю 0,95.
, то коефіцієнт а1 достовірний з ймовірністю 0,95. , то коефіцієнт а0 статистично не відрізняється від нуля.
, то коефіцієнт а0 статистично не відрізняється від нуля. , то наша прогнозна точка буде Х1=4,904. У таблиці 8.1 у стовпці 5 наведені розрахункові (теоретичне) значення отриманої регресії. Ми бачимо, що прогнозне значення Y=5,116.
, то наша прогнозна точка буде Х1=4,904. У таблиці 8.1 у стовпці 5 наведені розрахункові (теоретичне) значення отриманої регресії. Ми бачимо, що прогнозне значення Y=5,116. , то отримана нами економетрична модель
, то отримана нами економетрична модель  достовірна з ймовірністю 0,95. Так як R2=0,9285, то 92,85% вихідних даних підпорядковуються обраній регресії
достовірна з ймовірністю 0,95. Так як R2=0,9285, то 92,85% вихідних даних підпорядковуються обраній регресії 
 .
.