 ПОЗНАВАТЕЛЬНОЕ
| ПОДГОТОВКА И ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА.
ЛАБОРАТОРНАЯ РАБОТА № 18.2. ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ ВОЗДУХА И ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА. Цель работы: вычисление длины свободного пробега и эффективного диаметра молекулы азота (который составляет 78.1% воздуха) по коэффициенту внутреннего трения (вязкости). Приборы и принадлежности: цилиндрический сосуд с капилляром, стеклянный стаканчик, секундомер. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. Заметное отклонение молекул от прямолинейных траекторий при тепловом движении происходит только при их сближении. Такое взаимодействие между молекулами называется столкновением. Процесс столкновения молекул характеризуется величиной эффективного диаметра молекулы, т.е. это минимальное расстояние, на которое могут сблизиться центры двух молекул при их столкновении. Расстояние, которое проходит молекула между двумя последовательными столкновениями, называется длиной свободного пробега молекулы. В данной работе определяется средняя длина свободного пробега, так как длины пробегов отдельных молекул из-за статистического характера процессов в газах, естественно, должны отличаться. Молекулярно-кинетическая теория позволила получить формулы, в которых макроскопические параметры газа (давление, температура, объем) связаны с микропараметрами (размеры молекул, их масса, скорость). Из молекулярно-кинетической теории вытекает формула, связывающая вязкость со средней длиной свободного пробега молекул
где
Отсюда из формулы (1) получаем, что
Коэффициент вязкости можно получить, используя известную формулу Пуазейля для стационарного и ламинарного течения жидкости по капилляру:
где V — объем газа, протекающего через сечение трубки за определенное время t при определенной разности давлений r — радиус капилляра, l — длина капилляра Отсюда из формулы (3) найдем коэффициент внутреннего трения газа
При выводе этой формулы пренебрегаем кривизной капли вытекающей жидкости. Средняя скорость газовых молекул может быть найдена из закона распределения Максвелла:
`
где T — абсолютная температура,
Плотность газа можно найти из уравнения Клайперона-Менделеева:
где
Подставляя (4), (5), (6)в формулу (2),получим:
Эффективный диаметр молекулы можно вычислить из формулы, выражающей его связь с длиной свободного пробега молекулы:
где n — число молекул в единице объема при данных условиях, Д — эффективный диаметр молекулы. Число молекул в единице объема при данных условиях выражается формулой
где n0 — число Лошмидта – число молекул в единице объема при нормальных условиях (P0, T0). Тогда, используя формулы (8) и (9),получим выражение для эффективного диаметра молекулы газа:
где Т и Р — температура и давление окружающей среды.
ОПИСАНИЕ УСТАНОВКИ.
ПОДГОТОВКА И ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА. 1. Заполнить сосуд Д водой на 2/3 объема, плотно закрыть его пробкой. 2. Открыть кран Е и, дождавшись, когда вода начнет вытекать из сосуда каплями, подставить стаканчик, одновременно включив секундомер. 3. Измерить по шкале манометра высоту поднятия уровня воды (в момент начала появления капель). 4. Когда в стаканчике будет около 50-100 см3 воды, (этот объем займет воздух), перекрыть кран и остановить секундомер. Записать время истечения жидкости. 5. Разность давлений на концах капилляра рассчитать по формуле:
где 6. Температуру Т измерить комнатным термометром, а атмосферное давление Р определить по барометру. 7. По формулам (7) и (10)вычислить дину свободного пробега и эффективный диаметр молекулы азота. 8. Опыт повторить 3 раза с разными объемами, вытекающими из сосуда жидкости. Результаты измерений занести в таблицу № 18.2.1 9. Оценить возможные источники погрешности метода. Таблица № 18.2.1
КОНТРОЛЬНЫЕ ВОПРОСЫ. 1. Что такое ламинарное турбулентное течение жидкости? 2. Вывести формулы для длины свободного пробега молекулы и ее эффективного диаметра. 3. Как известно воздух состоит из смеси газов. Что следует понимать под 4. Почему коэффициент внутреннего трения жидкостей убывает с температурой, а у газов возрастает?
Радиус капилляра r = 0.54x10-3м, длина капилляра l = 75x10-3м. число Лошмидта n0 = 2,687 10 25 м - 3
|



 (1)
(1) — коэффициент внутреннего трения (динамическая вязкость)
— коэффициент внутреннего трения (динамическая вязкость) — плотность газа,
— плотность газа, — средняя длина свободного пробега молекул,
— средняя длина свободного пробега молекул, — средняя арифметическая скорость пробега молекул
— средняя арифметическая скорость пробега молекул (2)
(2) (3)
(3) на концах трубки,
на концах трубки, (4)
(4) (5)
(5) — молярная универсальная газовая постоянная,
— молярная универсальная газовая постоянная, — молярная масса газа.
— молярная масса газа. (6)
(6) — давление газа.
— давление газа.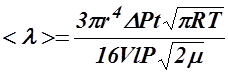 (7)
(7) (8)
(8) (9)
(9)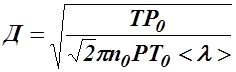 (10)
(10) Установка изображена на рис.18.2.1. Один конец капилляра К соединен с правым коленом манометра Ми атмосферой. Другой конец капилляра соединен со стеклянным баллоном Ди левым коленом манометра. При истечении воды из баллона Д, давление в нем понижается и в него через капилляр протекает воздух, объем которого за время t можно измерить.
Установка изображена на рис.18.2.1. Один конец капилляра К соединен с правым коленом манометра Ми атмосферой. Другой конец капилляра соединен со стеклянным баллоном Ди левым коленом манометра. При истечении воды из баллона Д, давление в нем понижается и в него через капилляр протекает воздух, объем которого за время t можно измерить.


 — плотность дистиллированной воды, при комнатной температуре (взять из таблицы); g —ускорение свободного падения.
— плотность дистиллированной воды, при комнатной температуре (взять из таблицы); g —ускорение свободного падения. , Па
, Па , м
, м