 ПОЗНАВАТЕЛЬНОЕ
| Задания для аудиторной работы
Историческая криптография Теоретические сведения История цивилизации показывает, что практически сразу с появлением письменности появлялись и разного рода системы защиты информации от несанкционированного доступа. Рассмотрим наиболее популярные из них. 1. Шифр Цезаря.Суть его в том, чтов текстекаждая буквазаменяется отстоящей от нее по алфавиту на фиксированное число позиций по циклу. Так Юлий Цезарь в I веке новой эры в деловой переписке заменял в сообщении первую букву латинского алфавита
Рис. 5.1 Пример 5.1. Знаменитое донесение римскому сенату об очередной победе выглядело (в русском переводе) следующим образом: ТУЛЫИО ЦЕЛЖЗО ТСДЗЖЛО Приложив достаточно серьезные усилия по расшифровке, можно убедиться, что истинный текст гласит: «Пришел, увидел, победил». Шифр Цезаря входит в класс шифров, называемых «подстановка» или «простая замена». Это такие шифры, в котором каждая буква алфавита заменяется буквой, цифрой, символом или какой-нибудь их комбинацией. 2. Тарабарская грамота. Известна в России с XIII века. На уровне разговорного языка ею владели и Стенька Разин и Емельян Пугачев. Гиляровский еще в 30-х г. ХХ века встречал на московских рынках странных лиц, переговаривавшихся между собой на «тарабарском». Тарабарская грамота проста. В ней согласные буквы заменяются по схеме, представленной на рис. 5.2.
Рис. 5.2
При шифровании буквы, расположенные на одной вертикали, переходят одна в другую. Остальные буквы остаются без изменения. Пример 5.2. Попробуйте прочитать следующее исключительно секретное сообщение: РАРА РЫСА МАРУ 3. Криптосистема Тритемиуса.Даннаясистема шифрования впервые была опубликована в 1518 г. в трактате, принадлежащем перу религиозного деятеля аббата Тритемиуса (1462 – 1516). Система Тритемиуса представляет собой дальнейшее усовершенствование системы шифрования Цезаря и базируется на идее применения девизов. Под текстом подписывался девиз (в дальнейшем его стали называть «ключом») с повторением, затем происходило постолбцовое суммирование букв текста и девиза («ключа»по новой терминологии), в результате получался шифротекст. Пример 5.3. Зашифруем текст «Над Парижем небо синее» с помощью девиза «Роза». Как сказано выше, для этого выпишем две строки – строку текста и строку ключа с повторением. Сверху и снизу добавим по строке номеров соотаетствующих букв в русском алфавите. Получим следующую таблицу (рис. 5.3).
Рис. 5.3 Для получения шифротекста суммируем числа каждого столбца полученной таблицы. Если сумма оказывается больше 33, то вычитаем из этой суммы 33. После этих вычислений от числа переходим к букве. Так в первом столбце получаем число
Французский посол в Риме Блез де Виженер (1523 – 1596), по роду службы связанный с проблемой секретности дипломатической почты, написал большой «Трактат о шифрах» (опубликован в 1585 г.). Он внес небольшое практическое усовершенствование в криптосистему Тритемиуса, которое позволило процедуру шифрования – дешифрования осуществлять почти автоматически. Роль шифровальной машины у Виженера играет квадратная таблица с алфавитом. Первая ее строка заполнена последовательно буквами алфавита. Вторая – тем же алфавитом, но сдвинутым на одну букву влево – в нашем случае начинается с буквы Б и заканчивается буквой А. Третья строка начинается буквой В и заканчивается буквой Б. И так далее, до 33 строки включительно. Возвращаемся к примеру 5.3. На пересечении столбца с первой буквой Н и строки с первой буквой Р находим букву Я – первую букву шифротекста. И так далее. В таком виде криптосистема с девизом применялась на протяжении 400 лет как абсолютно надежная и не дешифруемая, особенно в военном деле. О том, что криптосистема Тритемиуса успешно применялась и в начале ХХ века Таблица Виженера (1576 г.)
Опыт долгого применения рассмотренной криптографической системы указал на проблему ключей. Слишком долгое применение одного и того же ключа может навести противника на какие-то закономерности и, как следствие, к взлому криптосистемы. Проблема эта преодолевалась двумя путями. Сначала пришли к мысли применения длинных ключей. В идеале – длина ключа совпадает с длиной шифруемого текста. Затем, естественно, быстро пришли к идее частой смены ключей. Частая смена ключей порождают проблемы выбора новых ключей и их передачи. Выход был найден неожиданный и гениально простой – книга. Участники переписки используют идентичные экземпляры одного и того же издания конкретной книги. Новый ключ сообщается, называя страницу и абзац книги. Два числа переданные почтой или публикацией в рекламном отделе газеты вряд ли дадут содержательную информацию противнику. 4. Постолбцовая транспозиция.К классу «перестановка» относится шифр «маршрутная транспозиция» и его вариант «постолбцовая транспозиция». В данный прямоугольник Следующий пример демонстрирует шифрование методом «постолбцовой транспозиции».
Рис. 5.4 Шифрованный текст получается последовательной записью столбцов этой таблицы в строку, также змейкой, начиная с последнего: МАРЕЛ АБЕЦИ НИСИР УКПЛС КОУИС ЬЛБТС Конечно, возможны и другие способы-маршруты записи текста в таблицу и выписки столбцов.Например, такой, более естественный (рис. 5.5).
 Рис. 5.5
Попробуйте прочитать еще одно сообщение, шифрованное методом «постолбцовой транспозиции». Пример 5.5. МАСТ АЕРР ЕШРН ОЕРМ ИУПВ КЙТР ПНОИ Усложнением этих двух вариантов шифрования является применение девизов. Суть их в том, что после записывания текста в таблицу столбцы таблицы переставляются каким-то образом, прежде чем выписывать шифротекст. В человеческой природе свойственно всякому действию придавать какой-нибудь, пусть и призрачный, смысл. Вот и пришла кому-то мысль не просто переставлять столбцы, а в порядке следования букв в девизе. Пример 5.6. Усложним шифровку по первой таблице примера 5.4, применив к ней девиз «Немига». Согласно порядку следования букв в русском алфавите буквам этого девиза присваиваются соответственно следующие номера: 6, 3, 5, 4, 2, 1. В этом порядке и выписываем столбцы первой шифровки примера 5.4: СТБЛЬ РИСИН КОУИС УКПЛС ИЦЕБА ЛЕРАМ 5. Криптосистема Кардано.Пожалуй, наиболее сложный вариант «маршрутной перестановки» предоставляет поворотная решетка или решетка Кардано. Джероламо Кардано (1501 – 1576) – знаменитый итальянский математик, механик, врач, философ. Как математик, он знаменит тем, что нашел формулы решения кубических уравнений. А как механик – прежде всего тем, что на его идеях реализовано в каждом автомобиле устройство под названием «карданный вал». Наконец, Кардано оставил глубокий след и в криптографии. Авторству Джероламо Кардано принадлежит следующий метод шифрования. Для тайной передачи сообщения, содержащего
6. Аффинная система подстановок Цезаря.В системе шифрования Цезаря использовались только аддитивные свойства множества целых Определим преобразование в такой системе:
где а,b – целые числа, В аффинном шрифте каждой букве алфавита размера m ставится число из диапазона Следует заметить, что преобразование Например, пусть m=26, а=3, b=5. Тогда, очевидно,
Преобразуя числа в буквы английского языка, получаем следующее соответствие для букв открытого текста и шифротекста:
Исходное сообщение HOPE преобразуется в шифртекст AVYR Достоинством аффинной системы является удобное управление ключами - ключи шифрования и расшифрования представляются в компактной форме в виде пары чисел (а, b). Недостатки аффинной системы аналогичны недостаткам системы шифрования Цезаря. Аффинная система использовалась на практике несколько веков назад, а сегодня ее применение ограничивается большей частью иллюстрациями основных криптологических положений. 7. Криптосистема Хилла.Алгебраический метод, обобщающий аффинную подстановку Цезаря
для определения Множество целых • элементы кольца R образуют коммутативную группу относительно операции сложения; кроме того, существуют единичный и обратный элементы относительно операции сложения; • умножение и сложение удовлетворяют ассоциативному и дистрибутивному законам. Мультипликативное обратное a-1 элемента a кольца может существовать не всегда. Например, если модуль m = 26, то значения 2-1(mod 26) и 13-l(mod 26) не могут существовать. • Если модуль m является простым числом p, то существует обратная величина любого ненулевого элемента t из 1 £ t £ p-1. Множество Множество всех n-грамм
Линейное преобразование
которое удовлетворяет условию линейности
для всех s, t в Линейное преобразование
причем Базисом для векторного пространства Пусть Если векторы
где Например, когда m=26 и матрица преобразования
то определитель этой матрицы
удовлетворяет соотношению
Пусть Используем это преобразование Сначала разобьем n-грамму открытого текста на биграммы, причем выберем n кратным 2, например, 12-грамма PAYMOREMONEY делится на шесть биграмм: PA YM OR ЕМ ON EY. Затем в каждой биграмме открытого текста заменим каждую букву ее числовым эквивалентом (полагаем, что нумерация букв в алфавите начинается с 1): PA EM Преобразование биграмм Получаем:
Заменяя в биграммах шифртекста числа на соответствующие буквы, получаем 12-грамму шифртекста: YK JK UP BW IV LE. Для расшифрования биграмм Система Хилла является одноалфавитной в широком смысле слова. Если систему Хилла использовать для шифрования русскоязычного сообщения, то число 26 (количество символов в алфавите) нужно заменить на 33.
Задания для аудиторной работы Задание 5.1.Прочитать текст, записанный с помощью шифра Цезаря: а) еогфхя – ахс ефзёжг пгёв олщзжзмфхег; б) тусхлерцб фхсусрц ргжс еюфоылегхя, нгн дю срг рз дюог тусхлерг. Задание 5.2.Расшифровать «тарабарский» текст: а) ш гухой ропалкымь ло лшоир улкашор пе жоцяк; б) гко рохек лтафакь о передтой тсаллигелтой зисолозии рухгипа щеф нмонилти? Задание 5.3. Расшифровать текст, созданный с помощью таблицы Задание 5.4.Расшифровать сообщения, зашифрованные методом постолбцовой транспозиции: а) дбчргив ллуадны яёвваон онсдгчо снтартс коввуии огасбнм ропеаеа; б) бниен еоету зепдю рболв аррир саота стжеж уадлд днаьу. Задание 5.5. Расшифровать сообщения, зашифрованные по Кардано: иснктг опорид азвоон туанят нквсчи ооутяс
Задание 5.6.Расшифровать сообщения, зашифрованные методом аффинной подстановки Цезаря: а) с=кфнкыкпьуц пкхц йкукфцд итптйкыъё ытвтуъё дйъбкё, б) с=я шк хъкёо пгбгвщчя фкъёкп тгвфкъып убгвгбус , Задание 5.7.Расшифровать сообщения, зашифрованные методом Хилла, при условии, что линейное преобразование задается матрицей а) вшмнхящулхчящйтвэаео, б) озуфъесанеёоыохвзюдлжйфкыщ, 12 |



 на четвертую
на четвертую  , вторую
, вторую  – на пятую
– на пятую  , наконец, последнюю – на третью. Иными словами, замена производилась в соответствии с таблицей, которая в русском варианте имеет следующий вид (рис. 5.1).
, наконец, последнюю – на третью. Иными словами, замена производилась в соответствии с таблицей, которая в русском варианте имеет следующий вид (рис. 5.1).

 , то есть букву «Я». Продолжив процедуру, получим следующее шифрованное сообщение:
, то есть букву «Я». Продолжив процедуру, получим следующее шифрованное сообщение:
 вписывается сообщение по строкам. Шифрованный текст найдем, если будем выписывать буквы в порядке следования столбцов.
вписывается сообщение по строкам. Шифрованный текст найдем, если будем выписывать буквы в порядке следования столбцов. Пример 5.4.Текст, состоящий из 30 букв, записан построчно змейкой в таблицу или матрицу размером
Пример 5.4.Текст, состоящий из 30 букв, записан построчно змейкой в таблицу или матрицу размером  (рис. 5.4)
(рис. 5.4)
 букв, изготавливается трафарет из прямоугольного листа клетчатой бумаги размером
букв, изготавливается трафарет из прямоугольного листа клетчатой бумаги размером  клеток. В трафарете вырезают
клеток. В трафарете вырезают 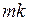 клеток так, чтобы при наложении его на такой же чистый лист бумаги четырьмя возможными способами его вырезы полностью покрывают всю площадь листа. Определяется заранее порядок этих четырех возможных положений. Буквы сообщения последовательно вписываются в вырезы трафарета – самый естественный вариант – по строкам, в каждой строке слева направо. Заполненная таблица записывается последовательно – каждый столбец в строку (рис. 5.6).
клеток так, чтобы при наложении его на такой же чистый лист бумаги четырьмя возможными способами его вырезы полностью покрывают всю площадь листа. Определяется заранее порядок этих четырех возможных положений. Буквы сообщения последовательно вписываются в вырезы трафарета – самый естественный вариант – по строкам, в каждой строке слева направо. Заполненная таблица записывается последовательно – каждый столбец в строку (рис. 5.6).
 . Однако символы множества
. Однако символы множества 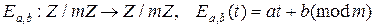
 ,
,  .
. . Затем буква, соответствующая числу t, заменяется на букву, соответствующую числовому значению
. Затем буква, соответствующая числу t, заменяется на букву, соответствующую числовому значению  по модулю
по модулю  .
. является взаимно однозначным отображением на множестве
является взаимно однозначным отображением на множестве  , равен единице, т.е. а и m должны быть взаимно простыми числами.
, равен единице, т.е. а и m должны быть взаимно простыми числами. , и мы получаем следующее соответствие между числовыми кодами букв:
, и мы получаем следующее соответствие между числовыми кодами букв:

 -грамм, был сформулирован Лестером С.Хиллом.
-грамм, был сформулирован Лестером С.Хиллом. (при m=p), поскольку значения t(mod m), 2t(mod m), 3t(mod m),.... (p-1) t (mod m) различаются, если
(при m=p), поскольку значения t(mod m), 2t(mod m), 3t(mod m),.... (p-1) t (mod m) различаются, если , где p – простое число, является примером алгебраической системы, называемой конечным полем. Ненулевые элементы
, где p – простое число, является примером алгебраической системы, называемой конечным полем. Ненулевые элементы  образуют мультипликативную группу.
образуют мультипликативную группу. с компонентами из кольца
с компонентами из кольца  над кольцом
над кольцом  называется вектором. В векторном пространстве
называется вектором. В векторном пространстве 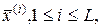 если
если (1)
(1) является отображением:
является отображением: ,
,  , (2)
, (2)
 в
в  может быть представлено матрицей размером
может быть представлено матрицей размером  вида
вида , (3)
, (3) или
или  .
. , которые линейно независимы и порождают
, которые линейно независимы и порождают 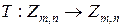 .
. линейно независимы над
линейно независимы над  линейно независимы над
линейно независимы над  , не делится на любое простое p , которое делит m (т.е.
, не делится на любое простое p , которое делит m (т.е.  :
: ,
,  , (4)
, (4) – единичная матрица. Кроме того,
– единичная матрица. Кроме того, 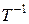 также является линейным преобразованием.
также является линейным преобразованием. ,
, . Поэтому существует обратное преобразование
. Поэтому существует обратное преобразование 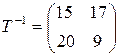
 .
. с матрицей
с матрицей  16 1; YM
16 1; YM  открытого текста в биграммы
открытого текста в биграммы  шифртекста осуществляется в соответствии с уравнением
шифртекста осуществляется в соответствии с уравнением 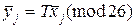 или
или  , где
, где  и
и  – вектор-столбцы биграмм шифртекста и открытого текста соответственно.
– вектор-столбцы биграмм шифртекста и открытого текста соответственно.
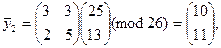
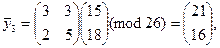



 шифртекста и восстановления биграмм
шифртекста и восстановления биграмм  . В рассмотренном примере матрицы преобразования имели размер
. В рассмотренном примере матрицы преобразования имели размер  и шифровались биграммы (пары) букв. Хотя буква Е может быть зашифрована по-разному в различных парах исходного сообщения, одна и та же пара, например ЕМ, будет шифроваться всегда одинаково на протяжении всего исходного текста.
и шифровались биграммы (пары) букв. Хотя буква Е может быть зашифрована по-разному в различных парах исходного сообщения, одна и та же пара, например ЕМ, будет шифроваться всегда одинаково на протяжении всего исходного текста.

 ;
; .
.