ПОЗНАВАТЕЛЬНОЕ
| Произведением двух событий А и В называется событие С, состоящее в совместном выполнении события А и события В.
Лабораторная работа № 2 По дисциплине «Математика и информатика» СЛУЧАЙНЫЕ СОБЫТИЯ. АЛГЕБРА СОБЫТИЙ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ. СУММА И ПРОИЗВЕДЕНИЕ ВЕРОЯТНОСТЕЙ Цель:получить представления о понятиях случайное событие, достоверное и невозможное событие, совместные и несовместные события, противоположные события, вероятность события, научиться определять сумму, произведение событий, вероятность события.
I. Случайные события и их классификация Под случайным событием понимается всякий факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: А – появление герба при бросании монеты (бросание монеты - опыт), В – попадание в цель при выстреле (выстрел - опыт), С – выпадение 3 очков при бросании игрального кубика. События бывают: а) достоверные и невозможные, б) противоположные, в) совместные и несовместные, г) зависимые и независимые. Достоверным событием называется такое событие, которое в данном опыте обязательно происходит. Невозможным событием называется такое событие, которое в данном опыте не может произойти. Задание 1. Среди событий найти достоверные и невозможные: А – выпадение четного числа очков при бросании игрального кубика, В – появление герба или числа при бросании монеты, С – появление герба и числа при бросании монеты. События Задание 2.Среди пар событий найти противоположные: 1) А – попадание при выстреле и С – промах при выстреле; 2) А – получение оценки «отлично» при сдаче экзамена и С – получение оценки «неудовлетворительно» при сдаче экзамена; 3) А – хотя бы одна пуля при двух выстрелах попала в цель и С – ни одна пуля при двух выстрелах не попала в цель. Два события называются несовместными, если при одном опыте появление одного из них исключает появление другого. Задание 3.Какие из следующих пар событий будут совместными, несовместными: 1) А – выпадение 2 очков при бросании игральной кости и С – выпадение 5 очков при том же самом бросании кости, 2) А – выпадение 3 очков при бросании игральной кости и С – выпадение нечетного числа очков при том же самом бросании кости, 3) А – попадание в цель и D – промах при том же выстреле. II. Сумма и произведение событий. Суммой двух событий А и В называется событие С, состоящее в выполнении хотя бы одного из событий А и В. Сумма обозначается А+В=С. На диаграмме Эйлера-Венна сумма двух событий А и В представляет собой заштрихованную область:
Задание 4.Опыт состоит в трех выстрелах по мишени и даны события: А0 – ни одного попадания, А1 – одно попадание, А2 – два попадания, А3 – три попадания. Записать события «не более одного попадания», «не менее двух попаданий». Задание 5.Из колоды карт достали две карты. Рассматриваются события А – первая карта пиковой масти, В – хотя бы одна карта черной масти. Чему равна сумма А+В? Произведением двух событий А и В называется событие С, состоящее в совместном выполнении события А и события В. Произведение обозначается АВ=С. На диаграмме Эйлера-Венна произведение двух событий А и В представляет собой заштрихованную область:
Задание 6.Студент отвечает на три вопроса экзаменационного билета. Событие А – студент знает ответ на первый вопрос, В – на второй вопрос, С – на третий вопрос. В чем состоят события АВС; АВ Задание 7.Опыт состоит в бросании двух монет. Рассматриваются события: А – появление герба на первой монете, В – появление герба на второй монете, E – появление хотя бы одного герба, F – появление хотя бы одной цифры, G – появление одного герба и одной цифры, H – непоявление ни одного герба, K – появление двух гербов. Составить события E, F, G, Н, K, комбинируя события А и В. III. Классическое определение вероятности. |



 называется противоположным событию А, если оно состоит в непоявлении события А.
называется противоположным событию А, если оно состоит в непоявлении события А.


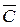 ;
;