 ПОЗНАВАТЕЛЬНОЕ
| Работа с Sim Power Systems
Лабораторная работа № 6 Тема: Исследование трехфазных цепей синусоидаль-ного тока Цель работы: Проверка основных соотношений в трехфазной системе при соединении приемников звездой и треугольником при равномерной и неравномерной нагрузке. Содержание работы 1. Исследование трехфазной цепи при соединении нагрузки звездой с нулевым проводом. 2. Исследование трехфазной цепи при соединении нагрузки звездой без нулевого провода. 3. Исследование трехфазной цепи при соединении нагрузки треугольником.
Порядок выполнения работы Задание 1. Исследование трехфазной цепи при соединении нагрузки звездой с нулевым проводом: - при равномерной загрузке; - при неравномерной загрузке; - при обрыве линейного провода;
Задание 2. Исследование трехфазной цепи при соединении нагрузки звездой без нулевого провода: - при равномерной загрузке; - при неравномерной загрузке; - при обрыве линейного провода; - при коротком замыкании фазы.
Задание 3. Исследование трехфазной цепи при соединении нагрузки треугольником: - при равномерной загрузке; - при неравномерной загрузке; - при обрыве линейного провода и равномерной нагрузке; - при обрыве линейного провода и неравномерной нагрузке; - при обрыве одного фазного провода источника; - при обрыве двух фазных проводов источника.
В заданиях 1 – 3 необходимо выполнить расчеты всех исследуемых параметров трехфазных цепей с помощью Control System Toolboox. Затем необходимо выполнить эксперименты с помощью приложения Matlab Sim Power System и сравнить расчетные данные с экспериментальными.
Модель для проведения экспериментов по заданиям 1 и 2 лабораторной работы представлена на рис. 1.
Рисунок 1. Модель исследования трехфазной цепи при соединении звезда-звезда После проведения моделирования на дисплее высвечиваются значения активных и реактивных мощностей в фазах А, В, С (рис. 1). Значения величин, измеренных блоком Powergui, показаны на рис.2.
Рисунок 2. Окно блока Powergui
Здесь кроме напряжений и токов в фазах нагрузки измеряются напряжение U0 и ток 10. Проведение всех опытов по пунктам заданий 1 и 2 осуществляются в соответствии с таблицей 1.
Таблица 1.
В отдельную таблицу (таблица 2) записываются начальные фазы всех измеряемых блоком Powergui начальных фаз для построения векторных диаграмм. Параметры источника питания и нагрузки задаются преподавателем или выбираются равными или близкими значениям, показанным в окнах (рис. 2 и 4 Приложения 2) при самостоятельном изучении. При неравномерной нагрузке в фазе А мощности устанавливаются в 1,2-1,8 раз больше, чем при равномерной нагрузке. Таблица 2
При проведении измерений без нулевого провода необходимо отсоединять от «земли» (ground) нейтральную точку (N) источника питания.
Испытание трехфазной цепи по заданию 3 осуществляется на модели, показанной на рис. 3.
Рисунок 3. Модель исследования трехфазной цепи при соединении звезда-треугольник
Здесь нагрузка соединена по схеме треугольника с включенными блоками измерения фазных токов (IAB,IBC,ICA) для блока Powergui. Окно настройки параметров нагрузки показано на рис. 2 Приложения 2. Следует еще раз напомнить, что в первом поле следует ввести значение напряжения, приложенного к нагрузке. Здесь, как видно из указанного выше рисунка, введено значение линейного напряжения источника питания. Активные и реактивные мощности в фазах нагрузки высвечиваются на экране дисплея (рис. 3). Фазные напряжения и токи, а также линейные токи определяются с помощью блока Powergui, окно которого показано на рис. 4.
Рисунок 4. Окно блока Powergui
Проведение всех опытов по заданию.3 осуществляется соответствии с таблицей 3.
Таблица 3
Параметры источника питания и нагрузки, а также мощность в фазе А при неравномерной нагрузке задаются также, как и в заданиях 1 и 2. В отдельную таблицу (таблица 4) записываются начальные фазы всех измеряемых блоком Powergui начальных фаз для построения векторных диаграмм.
Таблица 4
Параметры элементов трехфазных электрических цепей выбираются из таблицы 5. Таблица 5
Примечание: В случае, если расчетные и устанавливаемы параметры не стыкуются, допускается корректировка параметров с объяснением причины этой необходимости. Содержание отчета
1. Модели исследуемых электрических цепей с подключенными виртуальными измерительными приборами. 2. Расчетные формулы, использованные при анализе электрических цепей с определениями. 3. М-файлы программ расчетов цепей. 4. Заполненные таблицы. 5. Векторные диаграммы для всех пунктов работы. 6. Анализ полученных результатов и выводы по работе. Контрольные вопросы
1 Что называется многофазной системой и ее фазами? 2. В чем состоят преимущества многофазных электрических цепей перед однофазными? 3. Почему трехфазные электрические цепи получили наибольшее практическое применение? 4. Какая многофазная система ЭДС (напряжений, токов) называется симметричной? 5. Как обозначаются начала и концы обмоток трехфазных источников энергии? 6. Каковы основные особенности различных схем соединений трехфазных источников энергии? 7. Что такое последовательность фаз и как она определяется? 8. Каковы соотношения между линейными и фазными токами (напряжениями) в симметричной трехфазной цепи при соединении приемников энергии треугольником? 9. Каковы соотношения между линейными и фазными токами (напряжениями) в симметричной трехфазной цепи при соединении приемников энергии звездой? 10. Как рассчитать линейные и фазные токи в исследуемой системе при симметричной нагрузке? При несимметричной нагрузке? 11. Какие виды несимметрии бывают в трехфазных электрических цепях? 12. Как определить мощности в симметричной и несимметричной трехфазных цепях? 13. Можно ли получить симметричную трехфазную систему напряжений с помощью однофазных генераторов?
Приложение 1 Расчет трехфазных цепей
Общие положения и определения
Трехфазная цепь - это совокупность трех электрических цепей, в каждой из которых действует своя ЭДС, причем, все они одинаковы по величине и сдвинуты по фазе относительно друг друга на треть периода. Трехфазный генератор вырабатывает три ЭДС, которые записываются в комплексном виде следующим образом:
Обмотки генератора и нагрузка могут соединяться двумя способами: в звезду и треугольник.
1.1. Соединение в звезду
Для соединения потребителей ψψзвездой (рисунок 3.20)три их конца – X1, Y1, Z1соединяют в одну общую точку N1– нейтральную точку. Начало фаз приемника А1, В1, С1соединяют с началом обмоток генератора (А, В, С) проводами, называемыми линейными (АА1, ВВ1, СС1). Четвертый провод, соединяющий нейтральные точки генератора N и приемника N1, называется нейтральным. На схеме (рис. 1) изображена четырехпроводная цепь, где показаны условно положительные направления, принятые для всех токов и напряжений трехфазной цепи. ЭДС между началом каждой фазы генератора и его нейтральной точки называется фазной ЭДС генератора Для приемника фазные напряжения определяются так же, как и для генератора. Если пренебречь сопротивлениями всех линейных проводов, то потенциалы точек «А» и «А1», «В» и «В1», «С» и «С1» будут равны, поэтому в четырехпроводной цепи фазные напряжения приемника и ЭДС генератора всегда равны
Соотношение между линейными и фазными напряжениями определяются в общем случае по второму
Рис. 1. Схема соединения потребителя звездой
закону Кирхгофа (в геометрической или комплексной форме):
В симметричной цепи при несимметричной, когда
Ток бывает фазный и линейный: фазный – это ток в фазах генератора или приемника, линейный – это ток в линейных проводах. В звезде участки фаз генератора, линии и фаз нагрузки соединены последовательно, поэтому
В четырехпроводной цепи при отсутствии сопротивления в нулевом проводе токи могут быть найдены по закону Ома в комплексной форме
Угол сдвига фаз этих токов по отношению к соответствующим фазным напряжениям определяется характером нагрузки (активная, индуктивная, емкостная). Для симметричной нагрузки углы сдвига фаз обязательно равны между собой. Если применять второй закон Кирхгофа для узла N1 (рис. 1),то можно определить вектор нейтрального тока
или
При симметричной нагрузке сумма (3.47) равна нулю. Отсюда следует вывод: при симметричной нагрузке ток в нейтральном проводе отсутствует, поэтому необходимость в нем отпадает. При несимметричной нагрузке с нейтральным проводом токи в фазах, различны, но за счет нейтрального провода напряжение на каждой фазе приемника с изменением нагрузки практически остается постоянным и равным фазному напряжению генератора. Значит, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке. Активная мощность в несимметричной цепи трехфазного тока определяется как сумма мощностей отдельных ее фаз и мощность, рассеиваемая на нагрев нулевого провода
или когда сопротивлением нулевого провода можно пренебречь, или цепь симметрична:
или
где
при чисто активной нагрузке, при чисто реактивной нагрузке
а в остальных случаях имеет промежуточное значение. В симметричной цепи трехфазного тока активная мощность может быть найдена из выражений:
В случае, когда сопротивлениями в линейных и нейтральном проводах нельзя пренебрегать, расчет такой цепи может быть выполнен по любому известному методу, например, методу контурных токов.
Пример 1. Расчет трехфазной цепи соединенной в звезду методом контурных токов. Расчетная схема цепи изображена на рис. 2. Обозначения на схеме даны в соответствии с возможностью индексирования в MATLAB.
Рис. 2. Расчетная схема трехфазной цепи при соединении генератора и нагрузки по схеме звезда/звезда
Расчет сделан с учетом наличия некоторых сопротивлений в проводах линии и нейтральном проводе. В данном примере, для пояснения выводимых данных применена функция disp('ТЕКСТ'). Она позволяет в любом месте программы вывести на экран любой текст, введенный в нее и заключенный в кавычки. Данная функция может выводить только текстовые значения переменных, поэтому если необходимо вывести их числовое значение, то предварительно значение переменной следует преобразо вать в текстовый формат. Это достигается применением функции num2str(Sg). Функции dispи num2strпозволяют осуществить вывод рассчитанных значений переменных в удобной для восприятия форме, в строчку, как показано далее. В начале программы применен оператор clc, который каждый раз при выполнении программы очищает окно текущей сессии от старых данных, что весьма удобно на практике. В конце программы, помещен оператор clearall, который очищает все переменные и рабочее пространство программы, высвобождая тем самым, оперативную память. %Программа для расчета 3-х фазной цепи звезда/звезда %Расчет выполнен методом контурных токов clc % Очистка окна сессии перед выводом результатов решения % Исходные данные E=220; Zla=5+5*j; % Полное сопротивление линейного провода АА1 Zlb=5+10*j; % Полное сопротивление линейного провода ВВ1 Zlc=5+15*j; % Полное сопротивление линейного провода СС1 Zo=2+5*j; % Полное сопротивление линейного провода ОО1 Za=50+15*j; % Полное сопротивление фазы А Zb=50+15*j; % Полное сопротивление фазы В Zc=50+15*j; % Полное сопротивление фазы С % РЕШЕНИЕ % Определяем фазные и линейные напряжения генератора Ea=E; Eb=E*(-0.5-0.866*j); Ec=E*(-0.5+0.866*j); Eab=Ea-Eb; Ebc=Eb-Ec; Eca=Ec-Ea; % Вводим матрицы коэффициентов уравнений по законам Кирх- гофа A=[Zla+Za+ZoZoZo; ZoZlb+Zb+ZoZo; ZoZoZlc+Zc+Zo]; B=[Ea 0 0; Eb 0 0; Ec 0 0]; I=(A\B); disp('Линейные токи выводятся в следующем порядке:Ia, Ib, Ic, А') k=1:1:3; I=I(k,1) disp('Ток в нулевом проводе, Io, А') Io=I(1,1)+I(2,1)+I(3,1) % Определяем фазные напряжения и потери в линии disp('Фазные напряжения:Ua, Ub, Uc и смещение нуля Uo, В') Ua=Za*I(1,1) Ub=Zb*I(2,1) Uc=Zc*I(3,1) Uo=Zo*Io disp('Действующие значения фазных напряжений:Ua, Ub, Uc и смещения нуля Uo, В') Uda=abs(Ua) Udb=abs(Ub) Udc=abs(Uc) Udo=abs(Uo) disp('Потери в линии UIa, UIb, UIc, В') Ula=Zla*I(1,1) Ulb=Zlb*I(2,1) Ulc=Zlc*I(3,1) %Мощность генератора Sg, ВА: Sg=I(1,1)'*Ea+I(2,1)'*Eb+I(3,1)'*Ec; %МощностьнагрузкиSn, ВА: Sn=abs(I(1,1))^2*(Zla+Za)+abs(I(2,1))^2*(Zlb+Zb)+abs(I(3, 1))^2*(Zlc+Zc)+abs(Io)^2*Zo; Sb=Sg-Sn; disp([' Мощностьгенератора, ВАSg =',num2str(Sg)]) disp([' Мощностьнагрузки, ВАSn =',num2str(Sn)]) disp([' Балансмощности, ВАSb =',num2str(Sb)]) Id=[I(1,1) I(2,1) I(3,1) Io]; clear all
В результате выполнения программы имеем: Линейные токи выводятся в следующем порядке: Ia, Ib, Ic, А I = 3.5095 - 1.3145i -2.9873 - 2.1445i -0.11096 + 3.4861i
Ток в нулевом проводе, Io, А Io = 0.41126 + 0.027081i
Фазные напряжения: Ua, Ub, Uc и смещение нуля Uo, В
Ua = 195.19 - 13.085i Ub = -117.2 - 152.04i Uc = -57.84 + 172.64i Uo = 0.68711 + 2.1105i
Действующие значения фазных напряжений: Ua, Ub, Uc и смещения нуля Uo, В
Uda = 195.63 Udb = 191.96 Udc = 182.07 Udo = 2.2195
Потери в линии UIa, UIb, UIc, В
Ula = 24.12 + 10.975i Ulb = 6.5088 - 40.595i Ulc = -52.847 + 15.766i
Мощность генератора, ВА Sg =2185.6482+984.77636i Мощность нагрузки, ВА Sn =2185.6482+984.77636i Баланс мощности, ВА Sb =-4.5475e-013-4.5475e-013i 1.2. Соединение в треугольник
Если три фазы приемника с фазными сопротивлениями Так как при соединении треугольником к концам каждой фазы потребителя приложено линейное напряжение, то линейные напряжения будут являться одновременно и фазными, т. е.
Рис. 3. Схема соединение потребителей треугольником
Если пренебречь сопротивлениями линейных проводов, то фазные напряжения приемника равны соответствующим линейным напряжениям источника питания, а они практически неизменны.
.
Фазные и линейные токи не равны между собой, соотношение между ними можно получить по первому закону Кирхгофа, записанному для узлов схемы геометрической форме
Из уравнений (2) следует, что любой из линейных токов равен геометрической разности токов тех двух фаз нагрузки, которые соединяются с данным линейным проводом. Независимо от характера нагрузки геометрическая сумма линейных токов в трехпроводной цепи равна нулю:
Если сопротивления фаз приемника известны, то пренебрегая сопротивлением линейных проводов, величину фазных токов определяют по закону Ома
При симметричной нагрузке линейные и фазные токи равны по величине, причем
Активная и реактивная мощности определятся с учетом выражения(1) для симметричной цепи таким образом:
В случае, когда сопротивлениями в линейных проводах нельзя пренебрегать, расчет такой цепи может быть выполнен по любому известному методу, например, методу контурных токов. Пример 2. Расчет трехфазной цепи соединенной в треугольник методом контурных токов. Расчетная схема приведена на рис. 4.
Рис. 4. Расчетная схема трехфазной цепи при соединении нагрузки в треугольник для метода контурных токов
% Программа расчета цепи трехфазного тока звезда/треугольник % методом контурных токов % Исходные данные clc E=220; Zla=5+5*j; Zlb=6-3*j; Zlc=7+5*j; Za=50+50*j; Zb=75+20*j; Zc=45+10*j; % РЕШЕНИЕ % Определяем фазные и линейные напряжения генератора Ea=E; Eb=E*(-0.5-0.866*j); Ec=E*(-0.5+0.866*j); Eab=Ea-Eb; Ebc=Eb-Ec; Eca=Ec-Ea; % Вводим матрицы коэффициентов уравнений по законам Кирхгофа A=[(Zla+Zlc+Zc) -Zlc -Zc; -Zlc (Zlb+Zb+Zlc) -Zb; ZcZb-(Zc+Za+Zb)]; B=[(Ea-Ec) 0 0; (Ec-Eb) 0 0; 0 0 0]; I=(A\B); disp('Контурные токи выводятся в следующем порядке: I1, I2, I3, А') k=1:1:3; I=I(k,1) disp('Реальные токи будут равны, А:') Ia=I(1,1) Ib=-I(2,1) Ic=I(2,1)-I(1,1) Iab=I(3,1) Ibc=I(3,1)-I(2,1) Ica=I(3,1)-I(1,1) % Определяем фазные напряжения и потери в линии disp('Фазные напряжения:Ua, Ub, Uc, В') Ua=Za*Iab Ub=Zb*Ibc Uc=Zc*Ica disp('Действующие значения фазных напряжений:Ua, Ub,Uc, В') Uda=abs(Ua) Udb=abs(Ub) Udc=abs(Uc) disp('ПотеривлинииUIa, UIb, UIc, В') Ula=Zla*Ia Ulb=Zlb*Ib Ulc=Zlc*Ic %Мощность генератора Sg: Sg=Ia'*Ea+Ib'*Eb+Ic'*Ec; %МощностьнагрузкиSn: Sn=abs(Iab)^2*Za+abs(Ibc)^2*Zb+abs(Ica)^2*Zc+abs(Ia)^2*Zl a+abs(Ib)^2*Zlb+abs(Ic)^2*Zlc; Sb=Sg-Sn; disp([' Мощностьгенератора, ВАSg =',num2str(Sg)]) disp([' Мощностьнагрузки, ВАSn =',num2str(Sn)]) disp([' Балансмощности, ВАSb =',num2str(Sb)]) clearall В результате выполнения программы имеем: Контурные токи выводятся в следующем порядке: I1, I2, I3, А I = 7.6485 - 4.8642i 5.2643 + 3.5032i 3.9671 - 0.53968i
Реальные токи будут равны, А:
Ia =7.6485 - 4.8642i Ib =-5.2643 - 3.5032i Ic =-2.3842 + 8.3675i Iab =3.9671 - 0.53968i Ibc =-1.2972 - 4.0429i Ica =-3.6814 + 4.3245i
Фазные напряжения: Ua, Ub, Uc, В. Ua = 225.34 + 171.37i Ub = -16.431 - 329.16i Uc = -208.91 + 157.79i
Действующие значения фазных напряжений: Ua, Ub, Uc, В.
Uda = 283.1 Udb = 329.57 Udc = 261.8
Потери в линии UIa, UIb, UIc, В.
Ula = 62.564 + 13.922i Ulb = -42.096 - 5.2264i Ulc = -58.527 + 46.651i
Мощность генератора, ВА Sg =4785.6232+2153.9125i Мощность нагрузки, ВА Sn =4785.6232+2153.9125i Баланс мощности, ВА Sb =0-4.5475e-013i
Как видим, и в примере 1 и в примере 2 баланс мощности сошелся, значит, расчет выполнен, верно.
Приложение 2 Работа с Sim Power Systems
Виртуальные приборы и оборудование для проведения лабораторной работы представлены на рис. 1. Здесь в отличие от предыдущих лабораторных работ использованы три новых блока. 1. Трехфазный источник напряжения (Inductive source with neutral). 2. Однофазная нагрузка, задаваемая величинами активной и реактивной мощностей (Series RLC Load). 3. Блок измерения трехфазных напряжений и токов (Three-Phase V-IMeasurement).
Рис. 1. Виртуальные блоки для проведения лабораторной работы по трехфазным цепям
Окно настройки параметров трехфазного источника питания показано на рис. 2. В полях окна задаются амплитуда напряжения, начальная фаза напряжения фазы А, частота и внутренние параметры источника (сопротивление и индуктивность). Эти параметры задаются преподавателем и не изменяются при выполнении всех пунктов лабораторной работы. При самостоятельном изучении рекомендуется сохранить значения параметров такими, как на рис. 2.
Рис. 2. Окно настройки трехфазного источника питания
Окно настройки параметров блока измерения показано на рис. 3. Как следует из описания блока (рис. 3), для представления измеряемых значений в относительных величинах необходимо включить соответствующие флажки. Важнейшей особенностью применения данного блока является то, что измеренные им величины наблюдаются в блоке Powergui, т.е. этот блок может для определенных задач заменить блок Multimeter.
Рис.3. Окно настройки блока измерения в трехфазных цепях Окно настройки параметров нагрузки показано на рис 5.4. здесь задаются действующее напряжение и частота нагрузки, которые должны быть равны действующему напряжению и частоте источника, активная и реактивные мощности нагрузки.
Рис.4. Окно настройки параметров нагрузки
|







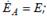


 ,
,  , а между началами фаз – линейными ЭДС генератора
, а между началами фаз – линейными ЭДС генератора  ,
,  ,
, 


 и
и при малых сопротив-лениях линейных проводов существует связь между линейными и фазными напряжениями:
при малых сопротив-лениях линейных проводов существует связь между линейными и фазными напряжениями:
 .
.



 ,
, ,
,
 ,
, ,
,  .
.
 ,
,  ,
,  , включить непосредственно между линейными проводами трехпроводной цепи, то получим соединение приемников треугольником (рис. 3).
, включить непосредственно между линейными проводами трехпроводной цепи, то получим соединение приемников треугольником (рис. 3). (1)
(1)

 .
. .
.
 .
.




