 ПОЗНАВАТЕЛЬНОЕ
| Описание метода и экспериментальной установки
Лабораторная работа 7.2.
ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ
Библиографический список 1.Трофимова Т. И. Курс физики. М.: Высшая школа, 1985. 2.Годжаев М. Н. Оптика. М.: Высшая школа, 1977. 3.Сивухин Д. В. Общий курс физики. Оптика. М.: Наука, 1980.
Цель работы: ознакомление с интерференционным явлением – кольцами Ньютона, представляющими собой так называемые полосы равной толщины. Приборы и принадлежности: осветитель, плоскопараллельная пластинка и плосковыпуклая линза, закрепленные в оправе, светофильтр, проекционная линза, экран. Описание метода и экспериментальной установки
Выпуклая поверхность линзы L (рис. 1) с большим радиусом кривизны R соприкасается в точке О с плоской поверхностью хорошо отполированной пластинки Е так, что остающаяся между ними воздушная прослойка постепенно утолщается от точки соприкосновения к краям. При нормальном падении на такую систему монохроматического света, световые волны, отраженные от нижней поверхности линзы и верхней поверхности пластинки, будут интерферировать между собой. При этом образуются интерференционные полосы, имеющие форму концентрических светлых и темных колец.
Так как между линзой L и пластинкой Е находится воздух
Условие минимума: Условие максимума: Условие возникновения темных колец выражено уравнением 2d = λk. Величина d может быть выражена через радиус кривизны линзы и радиус темного интерференционного кольца Однако эта формула не может быть применена для опытной проверки. Действительно, поскольку на поверхности даже очищенного стекла всегда присутствуют пылинки, то стеклянная линза не примыкает плотно к плоскопараллельной пластинке, а между ними имеется незначительный зазор величиной а. Из–за этого возникает дополнительная разность хода величиной 2а. Тогда условие образования темных колец примет вид
Подставляя значение d в уравнение для
Величина а не может быть измерена непосредственно, но ее можно исключить следующим образом. Для кольца m
Откуда
или окончательно
Зная длину волны и радиусы Установка, используемая в данном случае для измерения радиусов колец, изображена на рис. 2.
Здесь О – осветитель, S – система для получения колец Ньютона, L – линза для получения увеличенного изображения колец на экране, Ф – светофильтр, М – экран с миллиметровой бумагой для измерения радиусов колец, полученных на экране. Так как с помощью данной установки измеряются не радиусы самих колец, а радиусы их изображений на экране, необходимо учесть увеличение, даваемое линзой. Из геометрической оптики известно, что коэффициент увеличения
где Учитывая полученные соотношения (2), формулу (1) можно окончательно записать в следующем виде:
После определения среднего значения R необходимо найти доверительный интервал (величину ошибки в определении R), пользуясь известной формулой определения ошибки для косвенных измерений. Принимая в расчетной формуле
где Для нахождения ошибок 1. Определить погрешности отдельных измерений:
2. Вычислить квадраты погрешностей отдельных измерений ( 3. Определить среднеквадратичную погрешность результата серии измерений
4. Для выбранной надежности
5. Рассчитать погрешность измерения радиуса кривизны линзы – ΔR (при той же надежности α). Записать окончательный результат
6. Оценить относительную погрешность
Порядок выполнения работы 1. Включить осветитель. 2. Перемещением линзы добиться отчетливого изображения колец на экране. 3. Измерить расстояния f и d. 4. Зарисовать на миллиметровке 4 – 5 темных колец Ньютона для данной длины волны 5. Измерить диаметр каждого кольца 3 раза. 6. Результаты измерений занести в таблицу 1. 7. По итогам вычислений данных таблицы 1 заполнить 8. Группируя попарно радиусы колец Ньютона, рассчитать три раза радиус линзы R. 9. Определить относительную и абсолютную ошибки. Таблица 1
Таблица 2
Контрольные вопросы
1. Что такое интерференция? 2. При каком условии можно наблюдать интерференционную картину? 3. Что такое «полосы равной толщины» и «полосы равного наклона»? К какому случаю можно отнести полученную в данной лабораторной работе интерференционную картину? 4. Вывести формулу для радиусов темных и светлых колец. 5. Как изменятся радиусы светлых колец, если между линзой и плоскопараллельной пластинкой налить воду (n = 1,3). Считать, что показатель преломления линзы и пластинки больше, чем показатель преломления воды. 6. Можно ли получить кольца Ньютона, если вместо плоскопараллельной пластины использовать плосковыпуклую линзу? Чему в этом случае будут равны радиусы светлых колец, если линзы сделаны из одного и того же материала, их радиусы кривизны одинаковы и линзы находятся в воздухе?
|
При отражении световой волны от пластинки, оптическая плотность которой больше чем у воздуха, фаза волны изменяется на π, что эквивалентно уменьшению или увеличению оптической разности хода интерферирующих лучей на 
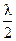. В месте соприкосновения линзы с пластинкой остается тонкая воздушная прослойка, толщина которой значительно меньше длины волны. Поэтому разность хода между лучами, возникающая в этой точке, определяется лишь потерей полуволны при отражении от пластинки, то есть 
. Следовательно, в центре интерференционной картины при наблюдении в отраженном свете будет темное пятно.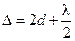
.
. Действительно, из рис. 1 видим, что 
. Если значение d мало по сравнению с R, то 
и, следовательно, 
.
, получаем
.
и следовательно,
(1)
и 
, (2)
- радиус кольца Ньютона в проекции на экране (увеличенный),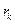 
- радиус кольца Ньютона, f - расстояние от полученного изображения до линзы (в данном случае – расстояние от экрана до линзы), d – расстояние от предмета до линзы (в данном случае – расстояние от системы, с помощью которой получаются кольца Ньютона, до линзы.
(3)
, m и k за постоянные величины, получаем для ошибки ΔR:
или
,
и 
- ошибки в определении 
и 
)2 и ( 
)2.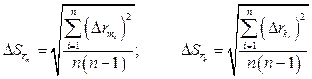
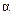найти t(α, n) и вычислить
и 
при 
.
, мм
, мм
, мм
, мм
, мм
, м
м
м
, м