ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Задачи повышенной сложности

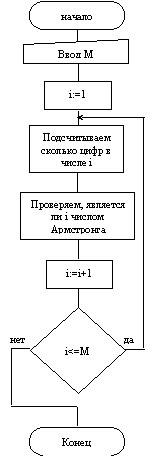
Лабораторная работа №3

Программирование циклических алгоритмов

Цель работы: закрепить практические навыки работы с системой Turbo Pascal, научиться правильно использовать различные операторы циклов; научиться составлять программы решения задач с использование циклических структур.

Общие сведения

Алгоритм называется циклическим, если он содержит многократное выполнение одних и тех же операторов при различных значениях промежуточных данных. Число повторений этих операторов может быть задано в явной (цикл с известным заранее числом повторений) или неявной (цикл с неизвестным заранее числом повторений) форме.

Перед выполнением работы необходимо изучить различные схемы организации циклов и операторы FOR, WHILE, REPEAT.

Примеры

Пример1: На промежутке от 1 до M найти все числа Армстронга. Натуральное число из n цифр называется числом Армстронга, если сумма его цифр, возведенных в n-ю степень, равна самому числу.

Этапы решения задачи:

1. Математическая модель: xО[1;M], x=

2. Составим блок схему программы:

Распишем составные части блока "Находим все числа Армстронга на заданном промежутке и печатаем их"

Опишем блок "Подсчитываем сколько цифр в числе i"

Опишем блок "Проверяем, является ли i числом Армстронга"

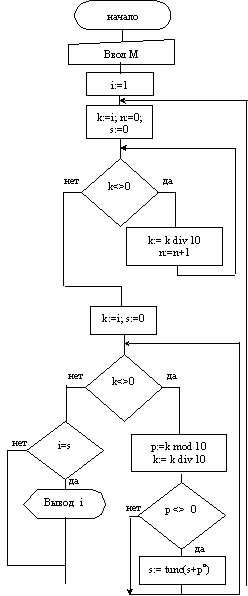
Дальнейшая детализация не требуется, запишем блок-схему целиком:

Дальнейшей детализации не требуется, переведем программу на язык Паскаль.

PROGRAM Primer_1;

var i,k,s,p,n: Integer;

BEGIN

Write('Введите M '); Readln(m);

For i:=1 to M do

begin

s:=0; k:=i; n:=0;

While k<>0 do

begin k:=k DIV 10; n:=n+1 end;

k:=i;

While k<>0 do

begin p:=k MOD 10; k:=k DIV 10;

If p<>0 then s:=Trunc (s+Exp(n*Ln(p)))

end;

If s=f then WriteLn (f)

end;

END.

Контрольные вопросы

1. Как записывается и как работает оператор FOR?

2. Для организации каких циклов применим оператор FOR?

3. В чем отличие оператора WHILE от оператора REPEAT?

4. Как программируются циклические алгоритмы с явно заданным числом повторений цикла?

5. Как программируются циклические алгоритмы с заранее неизвестным числом повторений цикла?

6. Напишите оператор цикла, который не выполняется ни разу.

7. Напишите оператор цикла, который выполняется неограниченное число раз.

8. Замените оператор "Repeat A Until B" равносильным фрагментом программы с оператором While.

Задачи

1.Дано натуральное n. Вычислить:
;

2.Дано натуральное n. Вычислить:

;

3. Дано действительное число х, натуральное число n. Вычислить:
x ( x - n )( x - 2 n )( x - 3 n )…( x - n2 );

3. Дано действительное число х, натуральное число n. Вычислить:
;

5. Дано действительное число х, натуральное число n. Вычислить:
;
6. Дано натуральное n. Вычислить:
;

7. Дано натуральное n. Вычислить:

;

8. Вычислить приближенно значение бесконечной суммы (справа от суммы дается ее точное значение, с которым можно сравнить полученный ответ):
= ;

9. Вычислить приближенно значение бесконечной суммы (справа от суммы дается ее точное значение, с которым можно сравнить полученный ответ):
= ;

10. Вычислить приближенно значение бесконечной суммы (справа от суммы дается ее точное значение, с которым можно сравнить полученный ответ):
= ;

Нужное приближение считается полученным, если вычислена сумма нескольких первых слагаемых, и очередное слагаемое оказалось по модулю меньше данного положительного числа e.

11. Найти все трехзначные числа, средняя цифра которых равна сумме первой и второй цифр.

12. Найти все двузначные числа, сумма квадратов цифр которых делится на 17.

13. Найти двузначное число, обладающее тем свойством, что куб суммы его цифр равен квадрату самого числа.

Задачи повышенной сложности

1. Определить, является ли заданное число совершенным , т.е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, число 6 совершенно: 6=1+2+3).

2. Дано натуральное k. Напечатать k-ю цифру последовательности 1234567891011121314..., в которой выписаны подряд все натуральные числа.

3. Дано натуральное k. Напечатать k-ю цифру последовательности 149162536..., в которой выписаны подряд квадраты всех натуральных чисел.

4. Дано натуральное k. Напечатать k-ю цифру последовательности 1123581321..., в которой выписаны подряд все числа Фибоначчи.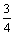