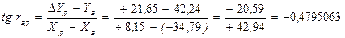ПОЗНАВАТЕЛЬНОЕ
| Исходные данные для решения задачи 1.
Отсчеты по рейкам и рулетке (а1, b1, a2, b2) принимаются одинаковыми для всех вариантов: а1=1142 мм, b1=8442 мм, а2=1684 мм, b2=1037 мм. Значение отметки репера (НRp) следует принять условно: количество целых метров в отметке должно быть трехзначным числом, в котором количество сотен метров равно единице, а количество десятков и единиц метров составляют две последние цифры шифра учащегося. В дробной части отметки (дм, см, мм) ставятся те же цифры, что и в целой части.
Пример: шифр – 82100 НRp=100,100 шифр – 82002 НRp=102,102 шифр – 82020 НRp=120,120 шифр – 81229 НRp=129,129 Задача 2 Определить высоту сооружения, если дано: расстояние от теодолита до сооружения 70,0 м. и отсчеты по вертикальному кругу теодолита Т30 КП КЛ т.А 180о05’ 7о27’ т.В 190о27’ 356о56’
Рис. 2 Схема определения теодолитом высоты сооружения
Для определения высоты сооружения (Н) от его основания до любого монтажного горизонта, необходимо установить теодолит так, чтобы хорошо были видны верх и основание здания. После чего измеряют углы наклона νА и νВ и расстояние – d – от инструмента до здания. Для определения углов наклона по вертикальному кругу теодолита сняты отсчеты: круг право на точку А, КПА=180о05’ круг право на точку В, КПВ=190о27’ круг лево на точку А, КЛА=7о27’ круг лево на точку В, КЛВ=356о56’ Углы наклона на каждую точку в отдельности вычисляем по формулам:
Высоту сооружения вычисляем по формуле: H=d∙ (tgνA - tgνB) Пример решения задачи 2 При решении задачи следует вычертить схему определения теодолитом высоты сооружения на рисунке 2.
d=70,0 м Вычисляем углы наклона по отсчетам вертикального КПА=180о05' круга теодолита Т30 по формулам: КПВ=190о27' КЛА=7о27' Примечание:при вычислении углов наклона к величи КЛВ=356о56' нам КП, КЛ меньше 90онеобходимо прибавлять 360о.
Н-? Высоту сооружения вычисляем по формуле: Н= d∙ (tgνA+tgνB) Н=70,0∙ (tg3о41' - tg(-6о45'30''))=12,8 м Ответ: Высота сооружения Н=12,8 м.
Исходные данные для решения задачи 2 Отсчеты по вертикальному кругу на точку А и точку В принимаются одинаковыми для всех вариантов: КЛА=358о06' КЛВ=9о03' КПА=171о54' ВПВ=170о56' Значение расстояния (d) от стоянки теодолита до сооружения следует принять: для вариантов 1-30 количество целых метров в расстоянии должно быть трехзначным числом, в котором количество сотен метров равно единице, а количество десятков и единиц метров составляют две последние цифры шифра учащегося. В дробной части расстояния (дм, см) ставятся те же цифры, что и в целой части.
Пример: Шифр – 82002 d=102,02 Шифр – 82020 d=120,20 Шифр – 81229 d=129,29 Для вариантов 31-100 количество целых метров в расстоянии должно быть двухзначным числом, в котором количество десятков и единиц метров составляют две последние цифры шифра учащегося. В дробной части расстояния (дм, см) ставятся те же цифры, что и в целой части.
Пример: Шифр – 82031 d=31,31 Шифр – 82050 d=50,50 Шифр – 82079 d=79,79 Шифр – 82100 d=100,100 Задача 3 Для вариантов 1-50 вычислить разбивочные элементы (dАС и β1), для выноса на строительной площадке точки -С- запроектированного сооружения от линии теодолитного хода с пунктами А и В, если координаты точек (ХАYA и ХСYС) даны в приложении 1, дирекционный угол αАВ=90о00'. Для вариантов 51-100 вычислить разбивочные элементы (dВД и β2), для выноса на строительной площадке точки -Д- запроектированного сооружения от линии теодолитного хода с пунктами А и В, если координаты точек (ХВYВ и ХДYД) даны в приложении 1, дирекционный угол αВА= αАВ+180о=90о00'+180о=270о00'.
Рис. 3 Разбивочная схема выноса точек запроектированного сооружения от линии теодолитного хода. Вынос проекта здания в натуру и разбивка для строительства здания – это два наименования одного и того же процесса геодезических работ, имеющего целью найти и закрепить положение на местности контура здания и его деталей, содержащихся в проекте. Опорой для определения местоположения точек и линий здания могут служить геодезические опорные пункты. При непосредственном использовании геодезических опорных пунктов, в том числе и пунктов теодолитных ходов, для разбивки полярным способом заданных точек С и Д необходимо выполнить следующее. 3.1. Вычислить дирекционный угол αАС (αВД) по координатам теодолитных точек А и В. Предварительно вычисляется румб линии АС или ВД по формулам:
Для определения угла румба, необходимо вычислить arctg от полученного значения румба. Дирекционный угол вычисляется исходя из формул зависимости дирекционных углов и румбов в таблице 1. Зависимость дирекционных углов и румбов Таблица 1
3.2. Вычислить горизонтальные углы β1 (β2) как разности дирекционных углов по формуле: β1= αАВ- αАС или β2= αВД- αВА
3.3. Вычислить горизонтальные расстояния dАС (dВД) от точек теодолитного хода по формулам:
Расхождение в горизонтальном расстоянии, вычисленном по трем формулам допускается с точностью до 0,1 м.
Пример решения задачи 3 При решении задачи 3 следует вычертить разбивочную схему (рис. 3) и после вычисления выписать на ней значения угла β1 (β2) и расстояния dАС (dВД).
Дано: ХВ= -34,79 м ХД= +8,15 м αАВ=90о00' YВ= +42,24 м YД= +21,65 м
Найти: β2, dВД
Решение: Вычислим приращения координат ΔХВД и ΔYВД, которые в дальнейшем будут использоваться в последующих формулах. ΔХВД=ХД- ХВ=+8,15-(-34,79)=+42,94 м ΔYВД= YД- YВ=+21,65-42,24=-20,59 м 3.1. Вычислим румб линии ВД
arctg(-0,4795063)= rВД=25о37'05’’: СЗ (IV четверть) Примечание:Числитель (Δу) имеет знак минус, а знаменатель (Δх) – плюс. Следовательно, румб имеет название СЗ (северо-запад), см. таблицу 1, а дирекционный угол равен: αВД=360о-rВД=360о-25о37'05''=334о22'55'' αВД=334о22'55''
3.2. Вычислим горизонтальный угол -β2- по формуле: β2=αВД-αВА; αВА=αАВ+180о=90о00'+180о00'=270о00' β2=334о22’55’’-270о00'=64о22'55''
3.3. Вычислим горизонтальное расстояние dВД по формулам:
Ответ: αВД=334о22'55''; dВД=47,622 м; β2=64о22'55''. |






 Дано: Решение
Дано: Решение



 или
или 
 или
или 
 или
или 
 или
или