 ПОЗНАВАТЕЛЬНОЕ
| Характеристичні швидкості кеплерівського руху
Закон всесвітнього тяжіння Фізичний закон, що описуєгравітаційну взаємодію в рамках Ньютонівської механіки. Закон стверджує, що сила притягання між двома тілами (матеріальними точками) прямо пропорційна добутку їхніх мас, і обернено пропорційна квадрату відстані між ними. Закон всесвітнього тяжіння сформулював Ісаак Ньютон у 1687 році у трактаті «Philosophiæ Naturalis Principia Mathematica». У математичній формі закон всесвітнього тяжіння записується дляматеріальних точок у вигляді:
де Для абсолютної величини сили:
Сила притягання, що діє на перше тіло з боку другого тіла однакова за модулем і направлена протилежно:
Інтеграл енергії Закон збереження енергії має вигляд: де h – стала, рівна повній механічній енергії, що відноситься до маси тіла, яке рухається. Оскільки 1) Характеристичні швидкості кеплерівського руху Для кожної відстані r від центрального тіла є дві характерні швидкості: перша при r = a – колова швидкість: При обертанні тіла по еліптичній орбіті , середня орбітальна швидкість співпадає з коловою швидкістю Для будь-якої планети середня швидкість Космічні швидкості Космічні швидкості є такими як : перша космічна швидкість, друга космічна швидкість, третя космічна швидкість і параболічна швидкість. Перша космічна швидкість це мінімальна космічна швидкість, при досягнені якої тіло знаходиться в гравітації, поле небесного тіла може стати його сопутником з круговою траекторією.Орбіта небесного тіла представляє окружність, еліпс, параболу або гіперболу, в фокусі яких є знаходиться центр мас системи. Пе́рша космі́чна шви́дкість — швидкість, яку, нехтуючи опором повітря та обертанням планети, необхідно надати тілу, для переміщення його на кругову орбіту, радіус якої рівний радіусу планети.Поняття першої космічної швидкості є досить теоретичним, оскільки реальні кораблі мають свій власний двигун і крім того, використовують обертання Землі. Для обчислення першої космічної швидкості необхідно розглянути рівність відцентрової сили та сили тяжіння, що діють на тіло на орбіті.
Дру́га космі́чна шви́дкість — мінімальна швидкість, яку необхідно надати тілу на поверхні планети (або іншого масивного небесного тіла), щоб воно вийшло за межі гравітаційної дії цієї планети. Для Землі друга космічна швидкість дорівнює 11,2 км/с. Друга космічна швидкість залежить тільки від маси планети, а не залежить від маси тіла, яке покидає її.
Між першою і другою космічними швидкостями існує просте співвідношення:
Третя космічна швидкість — мінімально необхідна швидкість тіла, що дозволяє перебороти тяжіння Сонця і в результаті вийти з Сонячної системи у міжзоряний простір.
Визначення мас небесних тіл Найбільш простий спосіб визначення мас небесних тіл базується на третьому обгрунтованому законі Кеплера : Вважаючи, що Обчислення ефемерид небесних тіл Знаючи положення планети на орбіті в будь-який момент t можна для всіх моментів обрахувати координати планети в будь-якій системі координат. Величини, що визначають рух планети називаються елементами її орбіти. Визначення видимих координат за елементами її орбіти називається обрахуванням ефемерид (наперед обчисленні координати планети ). , які у вигляді таблиць приводяться в астрономічному календарі. За основну площину приймають площину екліптики. 1. і – кут нахилу площини орбіти планети до площини екліптики. 2. l– геліоцентрична довгота висхідного вузла – кут в площині екліптики. 3. w – відстань від перигелія до орбіти – кут в площині орбіти планети. 4. а– величина півосі орбіти еліпса. 5. е– ексцентриситет оріти визначає ступінь стиснення еліпса. 6. Крім цих параметрів є й такі : істинна аномалія θ :
1. a Велика піввісь 2. е електронної ексцентриситету 3. і нахилу 4. Ω довгота висхідного вузла 5. ω Аргумент перигелію (або довгота перигелію π = ω + Ω) 6. T час перигелію проходження (або середня аномалія M) Відкриття Урана
Перші нечисленні спостереження ще не дозволяли досить точно визначити параметри орбіти нової планети, але, по-перше, кількість цих спостережень (зокрема, у Росії, Франції і Німеччині) швидко збільшувалося, а по-друге, уважне дослідження каталогів минулих спостережень дозволило переконатися, що планета неодноразово фіксувалася і раніше, але її вважали зіркою, що також помітно збільшувало число спостережень.Протягом 30 років після відкриття Урана гострота інтересу до нього то падала, то зростала. Справа в тому, що підвищення точності спостережень виявило загадкові аномалії в русі планети: він то «відставав» від розрахункового, то починав «випереджати» його. Теоретичне пояснення цих аномалій призвело до нового відкриття — відкриттяНептуна. |
,
— сила, що діє на друге тіло (матеріальну точку) з боку першого тіла, 
— гравітаційна стала, 
та 
— маси першого та другого тіла, відповідно, 
— одиничний вектор, що направлений в напрямку другого тіла від першого. 
— відстань між тілами.
.
.
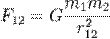Стала 
(1) ,
, то при 
рівняння (1) буде виконуватись для будь-яких r і рух необмежений у просторі. При h<0 рух обмежений у просторі. Величина ексцентриситету визначається значенням повної енергії і рівна: 
. Як бачимо з рівняння, можливі три види траєкторій: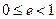
(h<0) – еліпс; 2) е = 1 (h=0) – парабола; 3) е >1 (h>0) – гіпербола.
, маючи яку тіло, що обертається, рухається по коловій орбіті; друга – параболічна швидкість 
, при якій тіло, що рухається, відходить від центрального тіла по параболі (а= 
). Очевидно, що 
.
, а – велика піввісь орбіти, Т – сидеричний період обертання. В будь-якій точці еліптичної орбіти на відстані r від центрального тіла тіло, що обертається має швидкість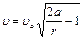 
.
, а у Землі 
. Для будь-якої планети 
. Знаючи, що 
а.о. , маємо :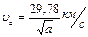 
.
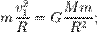
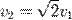
16,650км/с
, 
- маса планети, 
і 
- велика піввісь орбіти супутника і період його обертання навколо планети (визначають зі спостережень).Масою супутника в порівнянні з масою планети можна знехтувати. При визначенні мас планет в масах Землі порівнюють рух супутника планети з рухом Місяця навколо Землі.
- маса Землі, 
- зоряний місяць, 
- велика піввісь місячної орбіти, визначають масу планети в масах Землі. Якщо 
. Наприклад супутник Юпітера Калісто має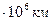 
, 
, тоді маса Юпітера в амсах Землі рівна 
.
- момент проходження планети через перигелій.
; ексцентрична аномалія Е :
r = a (1-e cosE) ;середня аномалія : М=Е-е сosE( 
)
Протягом багатьох сторіч астрономи Землі знали тільки п'ять «блукаючих зірок» — планет. Англійський астрономВільям Гершель, який взявся до реалізації грандіозної програми упорядкування повного систематичного каталога зоряного неба, 13 березня 1781 року помітив поблизу однієї із зірок сузір'я Близнят цікавий об'єкт, що, очевидно, не був зіркою: його видимі розміри змінювалися залежно від збільшення телескопа, а найголовніше — змінювалося його розташування на небі. Гершель спочатку вирішив, що відкрив нову комету (його доповідь на засіданні Королівського товариства 26 квітня 1781 року так і називався — «Повідомлення про комету»), але від кометної гіпотези незабаром довелося відмовитися. На подяку Георгу III, який призначив Гершеля королівським астрономом, він запропонував назвати планету «Георгієвою зіркою», проте, щоб не порушувати традиційного зв'язку з міфологією, було ухвалено назву «Уран».