 ПОЗНАВАТЕЛЬНОЕ
| айнымалы кернеуден пайда болды деп ескереміз.
Екені белгілі. L мен І-дің мәндерін (2.25)-ке қоятын болсақ:
мұндағы V = Sl – соленоид көлемі. Энергия соленоид ішіне топтасқан және тұрақты көлемдік тығыздықпен
4. Магнетиктер. Заттардағы магнит өрісі үшін толық ток заңы. Магнетиктердің магниттелу дәрежесі магниттеліну деп аталатын векторлық шамамен сипатталады. Магнетиктің бірлік көлеміндегі магнит моментін- магниттеліну деп атаймыз
мұндағы Магнит сезімталдылығы χ – заттардың сыртқы магнит өрісінің әсерінен магнит моментін өзгерте алу қабілеттілігін сипаттайтын физикалық шама. Егер магнит өрісінде зат болмаса, онда Ферромагнетиктерге сыртқы магнит өрісі жоқ болса да магниттік қасиетке ие болатын заттар жатады. Ферромагнетиктердің негізгі қасиеттері: 1. магниттік өтімділік өте үлкен мәндерге жетеді (106 -ге дейін); 2. магниттік өтімділік сыртқы магнит өрісінің кернеулігіне тәуелді, яғни магниттілік және магнит өрісінің кернеулігі арасындағы байланыс сызықты емес функция; 5. Электромагниттік өріс үшін Максвелл теңдеуілері. Уақыт өтуімен өзгеретін айнымалы магнит өрісі өзін қоршаған кеңістікте құйынды электр өрісін тудырады. 1.Максвелдің дифференциал түріндегі I-теңдеуі Тұйық бет арқылы өтетін кернеулік векторының циркуляциясы осы бетпен шектелген беттегі магнит өрісінің индукция векторының теріс таңбамен алынған өзгеру жылдамдығына тең болады.
2.Максвелдің дифференциал түріндегі II-теңдеуін аламыз Ығысу тогының тығыздығы электр өрісінің индукция (ығысу) векторының өзгеру жылдамдығына тең болады.
3.Максвелдің интеграл түріндегі III-теңдеуі заттардағы электр өрісі үшін Остроградский-Гаусс теоремасы болап табылады.
Максвелдің дифференциал түріндегі III-теңдеуі келесі түрде жазылады:
4.Максвелдің интеграл түріндегі IV-теңдеуі магнит өрісі үшін Остроградский-Гаусс теоремасы болап табылады.
Максвеллдің дифференциал түріндегі IV-теңдеуі
6. Электромагниттік толқындар және олардың қасиеттері. Электромагниттiк толқындар деп айнымалы электр өрiсiнiң және онымен байланысқан магнит өрiсiнiң кеңiстiктегi таралу процессiн айтады. Ал бұл өрiстер сәйкес электр өрiсiнiң кернеулiгi Электромагниттік толқындардың қасиеттерін толқын ұзындығы 3 см электромагниттік толқын шығаратын арнайы генераторды қолданып зерттейді. Аса жоғары жиілікті генератор қоздыратын электромагниттік толқын рупор түрінде таратқыш антеннада ось бағытымен шығарылады. Қабылдағыш антеннаның пішіні дәл таратқыш антеныа сияқты. Қабылдағыш антеннада кристалдық диод орнатылған, ол антеннада қозатын жиілігі жоғары айнымалы токты бір полярлы толықсыма тоққа айналдырады. Ток күшейтілгеннен кейін дыбыс қабылдағышқа немесе гальванометрге беріліп тіркеледі. 7. Электромагниттік өріс үшін толқындық теңдеу. Келтірілген (3.26)теңдіктеріне тағы да бір көңіл аударалық. Олар таралу бағытына перпендикуляр орналасқан жазықтықтың кезкелген нүктесіндегі электромагниттік өрістің сан мәндерінің бірдей екендігін көрсетеді. Электромагниттік ұйытқудың кеңістікте таралуын толқын деп атайтын болсақ, аталған жазықтықтың ең соңғысы толқын шебі (фронты) деп аталады. Электромагниттік ұйытқуды қарастырған кезде, электр және магнит өрістерінің кернеуліктері Е мен Н-тың координата х мен уақытқа t тәуелділігін ескере отырып, олар үшін төмендегідей теңдеулерді жазуға болады: (3.29) Келтірілген (3.29) теңдеуі ұйытқудың бір сызық бойымен таралу кездеріне ғана қолданылады, яғни олар Е=f(x,t) мен Н= j(x,t) функцияларын анықтайды. Олардың айқын түрлері осы теңдеулерді шешу кезінде аталмыш функцияларға қойылатын шектерге және бастапқы шарттарға байланысты. Мысалы, бастапқы ток – электромагниттік толқудың көзі – гармониалық заңдылықпен өзгеретін болса (І=І0×cosωt), онда (3.29) теңдеуінің шешімі:
мұндағы Е0 мен Н0 – өрістердің амплитудалық мәндері; w – тербелістің циклдік жиілігі; v – электромагниттік толқынның жылдамдығы. Осы теңдіктер жазық электромагниттік толқындар теңдеулері деп аталады. Олар Осыған дейін біз, (3.26) теңдікті қарастыра отырып,
8. Электромагниттік толқын энергиясы. Электромагниттік энергия ағынының тығыздығы. Умов-Пойнтинг векторы. Электромагниттік толқын таралған кезде энергия тасымалданады. Қайсыбір бет арқылы бірлік уақытта толқын тасымалдайтын энергия мөлшері энергия ағыны деп аталады және ол Ваттпен өлшенеді. Кеңістіктің әртүрлі нүктелеріндегі энергия ағысын сипаттау үшін энергия ағынының тығыздығы деп аталатын векторлық шама енгізіледі. Бұл шама берілген нүктеге энергияның тасымалдану бағытына перпендикуляр орналастырылған бірлік аудан арқылы өтетін энергия ағынына сан жағынан тең. Энергия ағыны тығыздығы векторының бағыты энергияның тасымалдану бағытымен дәл келеді. Энергия ағыны тығыздығының векторын серпімді толқындар үшін 1874ж. қарастыруға алғаш енгізген Н.А.Умов (1846-1915). Ол кез-келген ортадағы энергия ағыны жайындағы жалпы теореманы дәлелдеді, Умов векторы мынаған тең
9. Электрлік тербелмелі контурдағы еркін тербелістің дифференциалдық теңдеуі. Томсон формуласы. тербелмелі контур – тізбектей қосылған индуктивтігі l шарғы (катушка), электрлік сыйымдылығы c конденсатор және электрлік кедергісі r резистордан құралған тізбек – электрмагниттік тербелістерді қоздыру және орнықтыру (электр өрісінің энергиясын магнит өрісінің энергиясына және керісінше түрлендіретін периодты процестер) үшін қолданылады. электрмагниттік тербелістердің теңдеуі идеал контурда (r=0) еркін электрлік тербелістер гармоникалық сипатта болады. осы жағдайда кирхгофтың екінші ережесі бойынша:
мұндағы :
контурдағы заряд тербелістерінің дифференциалдық теңдеуі:
дифференциалдық теңдеудің шешімі зарядтың өзгеру заңдылығын анықтайды:
мұндағы : өшпейтін еркін тербелістердің периоды (томсон формуласы):
10. Электрлік тербелмелі контурдағы еркін өшетін тербелістің дифференциалдық теңдеуі. Өшудің логарифмдік декременті. контурдағы зарядтың еркін өшетін тербелістерінің дифференциалдық теңдеуі:
мұндағы дифференциалдық теңдеудің шешімі зарядтың өзгеру заңдылығын анықтайды:
зарядтың тербелісі гармоникалық емес (60-сурет). өшудің аз мәндерінде ( өшудің логарифмдік декременті:
мұндағы 11. Мәжбүр электромагниттік тербелістің дифференциалдық теңдеуі. Резонанс. электрмагниттік мәжбүр тербелістер – гармоникалық заң бойынша периодты өзгеретін сыртқы мәжбүр тербелістердің дифференциалдық теңдеуі:
ток резонансы (параллель резонанс) – сыртқы айнымалы кернеудің циклдік жиілігінің тербелмелі контурдың меншікті жиілігіне жуықтағанда өзара параллельажалғанған конденсатор мен шарғыны қоректендіретін сыртқы тізбектегі ток күшінің амплитудасының күрт кему құбылысы 12. Айнымалы ток. Айнымалы ток үшін Ом заңы. Орныққан еріксіз тербелісті сыйымдылық, индуктивтік және актив кедергісі бар тізбектен айнымалы токтың өтуі деп қарастыруға болады, ол U = Um coswt (3.66) айнымалы кернеуден пайда болды деп ескереміз. Айнымалы токтың толық тізбегі үшін Ом заңы [өңдеу] Бір-біріне тізбектей жалғанған индуктивтігі
13. Айнымалы токтың қуаты. Айнымалы ток тізбегінде берілген уақыт мезетіндегі қуат ток күші мен кернеудің лездік мәндерінің көбейтіндісіне тең.
Бұл өрнекті түрлендіріп
Бізге бір период ішіндегі орташа қуатты анықтау керек. Ол үшін уақытқа тәуелді тригонометриялық функциялардың орташа мәндерін табайық:
Олай болса, қуатты анықтайтын өрнектегі екінші қосылғыштың орташа мәні нөлге тең. Сонымен, айнымалы ток тізбегінде орташа қуат:
Бұл теңдеуге ток пен кернеудің әсерлік мәндерін қойып, ыңғайлы болу үшін әсерлік мәндердің индексін жазбай
шығады. (2.18) мен (2.19) өрнектеріндегі 14. Геометриялық оптиканың негізгі заңдары. Жарықтың түзу сызықты таралу заңы: жарық сәулелері біртекті ортада түзу сызық бойымен таралады. Күннің, айдың тұтылуларын бақылау, көлеңкелердің пайда болуы жарықтың түзу сызықты таралатындығын көрсетеді. Жарықтың түзу сызықты таралу заңы геометриялық оптикада негізгі заң болып табылады. Бірақ бұл заңның сәулелер бөгеуші қалқалардың (экранның) жақын маңайынан өткен жағдайда орындалмайтындығы тәжірибеде байқалды. Мұнда біз физикалық оптикада (1-бөлім) толық қарастырылғандифракцияқұбылысымен ұшырысамыз. Геометриялық оптикада дифракция құбылысы қарастырылмайды. Бірақ оптикалық аспаптар теориясында әрқашан осы құбылыс есепке алынады, өйткені оптикалық жүйелерде жарық шоқтарының едәуір ықшамдалуынан (диафрагмалануынан) дифракция пайда болуы мүмкін, бұл кескіннің бұзылуын тұғызады. Бұл заңды дифракция құбылыстары есепке алынбайтын жағдайларда ғана қолдануға болады. Жарық шоқтарының тәуелсіздік заңы: жарықтың бір шоғының әсері басқа шоқтарының әсерлеріне тәуелді емес, яғни жарықтың жеке сәулелері мен шоқтары бір-бірімен түйіскенде, қиылысқанда бір-біріне ықпалын тигізбейді. Шындығында, кейбір жағдайларда кескіннің нүктелеріндегі жарықталудың қайта үлестірілуін туғызатын интерференция құбылысы орын алады. Интерференция физикалық оптикада қарастырылады. Бірақ кескіннің түзілу теориясында интерференцияның маңызды мәні бар, өйткені ол шашырау дағындағы жарық энергиясының үлестірілуін түсіндіреді; бұл өз кезегінде кескін сапасы жайында қорытынды жасауға мүмкіндік береді. Демек, бұл заң когерент емес жарық шоқтары үшін дұрыс орындалады. Жарықтың шағылу заңы: бетке түскен сәуле, одан шағылған сәуле және сол бетке сәуленің түсу нүктесі арқылы жүргізілген нормаль бір жазықтықта жатады; шағылу бұрышы түсу бұрышына тең: α=α1(4.1) Жарықтың сыну заңы: түскен сәуле, сынған сәуле және түсу нүктесі арқылы екі ортаның шекара бетіне жүргізілген нормаль бір жазықтықта жатады; түсу бұрышы синусының сыну бұрышы синусына қатынасы берілген екі орта үшін тұрақты шама болады:
мұндағы n21- екінші ортаның бірінші ортаға қатысты сыну көрсеткіші, ол шекарасынан жарық өтетін орталардың қасиеттеріне тәуелді, α мен β бұрыштарының үлкен – кішілігіне байланысты емес. Жарықтың осылай тұжырымдалған сыну заңы жарық бір изотроп ортадан екінші изотроп ортаға өткенде ғана орындалады. 15. Шағылу және сыну заңдары. Толық ішкі шағылу. Жарықтың шағылу заңы: бетке түскен сәуле, одан шағылған сәуле және сол бетке сәуленің түсу нүктесі арқылы жүргізілген нормаль бір жазықтықта жатады; шағылу бұрышы түсу бұрышына тең: α=α1(4.1) Жарықтың сыну заңы: түскен сәуле, сынған сәуле және түсу нүктесі арқылы екі ортаның шекара бетіне жүргізілген нормаль бір жазықтықта жатады; түсу бұрышы синусының сыну бұрышы синусына қатынасы берілген екі орта үшін тұрақты шама болады:
мұндағы n21- екінші ортаның бірінші ортаға қатысты сыну көрсеткіші, ол шекарасынан жарық өтетін орталардың қасиеттеріне тәуелді, α мен β бұрыштарының үлкен – кішілігіне байланысты емес. Жарықтың осылай тұжырымдалған сыну заңы жарық бір изотроп ортадан екінші изотроп ортаға өткенде ғана орындалады. Толық ішкі шағылу: 16. Линзалар және оның негізгі сипаттамалары. Жұқа линзаның формуласы. Сфера бетпен немесе сфера беттің бөлігімен шектелген ортаны линза д/а.Линзаларды шектейтін сфералардың центрлері арқылы өтетін түзуді бас оптикалық ось д/а.Линзаның ортасында орналасқан нүктені линзаның оптикалық центрі д/а. Линзаның оптикалық центрінен өтетін жарық сәулелерінің бағыты өзгермейді. Ортасына қарай жуандайтын линза жинағыш линза д/а. Ал ортасынан шетіне қарай жуандайтын линза шашыратқыш линза б/т. Сонымен қатар линзалар шектелген беттердің формасына қарай қос дөңес, қос ойыс, дөңес-ойыс, жазық – дөңес, жазық-ойыс түрлеріне бөлінеді. Аа а) б) в) г) д) Суреттегі а,в,г – жинағыш линзалар, б,д – шашыратқыш линзалар. Жарық сәулелері оптикалық жүйеде сынғаннан кейін сол жарық сәулелерінің өздері немесе олардың созындылары қиылысатын F нүктелері олардың фокустары д/а. Нәрседен линзаға дейінгі қашықтықты - d, ал линзадан кескінге дейінгі қашықтықты – f десек, линзаны шектеп тұрған беттердің қисықтық – радиустары линзаның қалыңдығынан анағұрлым үлкен болатын жұқа линза үшін мына теңдік орындалады: 1/d + 1/f = + - 1/F. Мұндағы + таңбасы жинағыш линза, ал – таңбасы шашыратқыш линзалар үшін қолданылады. Теңдеудің оң жағындағы шаманы линзаның оптикалық күші д/а, яғни D=1/F. Оның өлшемі диоптрия, 1дптр =1 м-1 . 17. Жинағыш және шашыратқыш линзалардағы нәрсенің кескінін тұрғызу. Линза - екі сфералық беттермен шектелген мөлдір дене. Жұқа линза қалыңдығы қисықтық радиусымен салыстырғанда өте аз линза.
18.
Бас оптикалық ось (О1, О2) ‒ линзаның сфералық беттерінің центрлері арқылы өтетін түзу. Қосымша оптикалық остер ‒ линзаның оптикалық центрі арқылы өтетін кезкелген түзу. Оптикалық центр (О) ‒ бас оптикалық осьпен линзаның қиылысу нүктесі. Фокус (F) ‒ линзаның бас оптикалық осіне параллель түскен сәулелердің сынғаннан кейін бас остің бойында жиналған нүктесі (жинағыш линза). Жалған фокус (F´) ‒ линзаның бас оптикалық осіне параллель түскен сәулелердің сынғаннан кейінгі сәулелерінің созындыларының қиылысу нүктесі (шашыратқыш линза). Линзадан кескін салу 1. Оптикалық центр арқылы өтетін сәуле сынбайды (бағытын өзгертпей линзадан өтеді). 2. Бас оптикалық оске параллель түскен сәуле сынғаннан кейін фокус арқылы өтеді (сынғаннан кейін сәулелердің созындылары жалған фокус арқылы өтеді). 3. Фокус арқылы түскен сәуле, бас оптикалық оске параллель өтеді.
Шашыратқыш линза нәрсенің кез-келген орналасуында кішірейген, жалған, тура кескін береді. 28. Фотометрлік шамалар және олардың өлшем бірліктері. Жарықталыну заңы. Жарықтың интенсивтігімен және жарық көзімен немесе жарық ағындарымен және олармен байланысты шамалармен айналысатын оптика бөлімін фотометрия деп атайды. Жарықтың интенсивтігі тасымалданатын энергиямен сипатталады. сәулелену энергиясының ағыны деп
шаманы айтады. Қолданбалы есептерді шешу кезінде көзге жарық әсерінің толқын ұзындығына тәуелділігі есепке алынады. Мысалы, 3500С-қа дейін қыздырылған дене инфрақызыл сәулелерді жақсы шығаратын жарық көзі болып табылады, бірақ олар адам көзіне көрінбейді және олардың субъективті түйсігі нолге тең болады. Толқын ұзындығы Жарықталыну Е деп бетке түсетін
Жарықталынудың өлшем бірлігі – «люкс» (лк). Нүктелік жарық көзі жасайтын жарықталынуды жарық күшімен
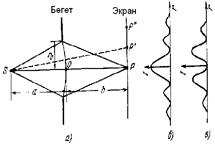
мұндағы (4.17) өрнегі нүктелік жарық көзі үшін жарықталыну заңы (немесе Ламберт заңы) деп аталады. 1. Жарық толқындарының интерференциясы. Оптикалық жол айырымы мен фазалар айырымы арасындағы байланыс. Интерференциялық максимум және минимум шарттары. Экранға жарық түскен кезде, жарық интенсивтігі біркелкі таралмай, ол максимал және минимал жарықталған жолақтармен ауысып, экранда интерференциялық сурет пайда болатындығы байқалады, яғни интерференция құбылысы пайда болады, кеңістіктің кейбір нүктелерінде когерентті жарық толқындарының бір-біріне беттесуі, кеңістіктің көрші нүктелеріндегі жарық энергиясының (интенсивтігінің) ағынының қайта орналасуына әкеледі. Кеңістіктің кейбір Р нүктесінде бір мезетте екі монохромат толқын пайда болсын (жалпы жағдайда олар монохроматты болмауы да мүмкін), олардың кернеуліктері
оның интенсивтігі,
ал мұндағы
Бұл бөліктер бір ғана толқынның бөлігі, олай болса,
мұндағы
Интерференциялық максимум
Осыдан
Интерференциялық минимум
онда яғни Қорыта айтқанда, максимум немесе минимумның болу шарты оптикалық жол айырымдарының мәні жұп немесе тақ жарты толқын ұзындығының мәніне тең болуына тәуелді болады. 2. Екі когерентті көздерінен алынған жарық интерференция. Интерференциялық жолақтың ені. Толқындық процестердің бір-бірімен сәйкесті өтуін когеренттілік деп атаймыз. Жарық толқындарының когерентілігі екі түрлі болады: уақыт және кеңістік бойынша когеренттілік. Тәжірибеде, уақыт бойынша когеренттілікті жарық толқынының монохроматтық дәрежесімен анықтаса, ал кеңістіктік когеренттілікті эксперименттік қондырғының белгілі бір өлшемдерімен анықтайды. Жоғарыда біз мынадай:
гармоникалық толқындардың интерференциясын қарастырған болатынбыз. Әрине, мұндай толқындар – абстракция. Нақты толқындар болса, амплитудасы Е0, фазасы
Физикалық процестер өткен кезде квази монохромат толқын үшін, оның амплитудасы Уақыттық когерентілікке когеренттік ұзындық тәуелді – толқын
Қарапайым жарық көздері үшін, оның шамасы 3¸30 см болса, лазер көзі үшін ~ 1км, тіптен одан да үлкен болуы мүмкін. Анық интерференциялық бейне жарық толқындарының мынадай шамасында пайда болады.
Қарастырып отырған тәжірибеде көрінетін жолақтардың саны шектеулі, себебі
бұдан жарық толқынында 3. Жазық параллель пластинадан алынған жарық интерференция. Бірдей көлбеулік жолақтары. Екінші сынған сәуле В нүктесінде шағылып, С нүктесінде сынып пластинкадан ауаға қайта шығады, ол шағылған 1 сәулеге параллель болады. Л линза бағытында жүрген жарық шоғында СД толқын фронтын жүргіземіз. Сонда шеткі 1-2 сәулелерінің арасындағы сәуленің оптикалық жол айырымы мынаған тең болады:
мұндағы n − пластина затының сыну көрсеткіші, − бірінші сәуле оптикалық тығыз ортадан шағылғанда өзінің фазасын қарама-қарсы бағытқа ауыстырады (p-ға тең шамаға), соған қосымша қосылғыш. Интерференциялық бейне тек уақыттық және кеңістіктік когеренттік шарттарын сақтағанда ғана байқалатындығы табиғи нәрсе. Бұл жағдайда пластина қалыңдығы мына шартты қанағаттандыруы керек
мұндағы 4. Бірдей қалыңдықты жолақтар. Ньютон сақинасы. Егер жұқа пластинканың беттері бір-біріне параллель болмаса, онда бұларды аумақты жарық көзімен жарықтандырған кезде тұрақты оптикалық қалыңдық жолақтары, немесе бірдей қалыңдық жолақтары пайда болады. Бірдей қалыңдық жолақтарын қалқаға (экранға) пластина бетінің кескіні проекцияланған жағдайда бақылауға болады. Сурет
Жазық-дөңес линза мен жазық шыны пластинка арасындағы ауа қабатында пайда болатын бірдей қалыңдық жолақтарының мысалына Ньютон сақиналары жатады. Ньютон заманында сақиналардың пайда болуын түсіндіру өте қиын болды. Мәселен, Гук сақиналардың түзілу себебін интенсивтігі әртүрлі шағылған екі шоқтың болуынан көрді, ал Ньютон сақиналардың пайда болуы линзаның қисықтық радиусына тәуелді болатындығын тағайындады. Тек кейіннен (1802 ж) Юнг интерференция ұғымын енгізіп, осы құбылысты түсіндірді. Ньютон сақиналары қисықтығы аз линзаның дөңес беті шыны пластинаның жазық бетімен қайсыбір нүктеде түйіскен жағдайда, бұлардың араларындағы түйісу нүктесінен шеттеріне қарай біртіндеп өсетін, сына пішіндес ауа қабатында пайда болады (2-сурет). Линзаға монохроматты жарық ағыны тік түсетін болсын. Сонда жарық толқындарының ауа қабатының үстіңгі және астыңғы шекараларынан шағылуы нәтижесінде интерференция байқалады. Шағылған жарықта бақылағанда түйісу нүктесінде қараңғы дақ болады да, ал оны ені кеміп отыратын жарық және қараңғы концентрлік сақиналар жүйесі қоршап тұрады. Орталық қараңғы дақ геометриялық жүріс айырымы нөлге тең болатындықтан және жазық шыны пластина бетінен шағылған кезде жарты толқынның жоғалуы нәтижесінде пайда болады. Өткен жарықтағы интерференциялық көрініс шағылған жарықта байқалатын көрініске қосымша көрініс, яғни бір жағдайдағы жарық жолақтар екінші жағдайда қараңғыға ауысады. 2-суреттен тиісті сақина радиусы үшін өрнекті алуға болады 5. Жарық дифракциясы. Гюйгенс-Френель принципі. Жарықтың дифракциясы - деп біртекті емес ортада (мәселен, экрандағы тесіктерден және мөлдір емес шекара маңында) таралғанда байқалатын жарықтың толқындық қасиетттерінің жиынтығын айтамыз. Дифракция құбылысы кезінде жарық толқындары бөгеттерді айналып өтіп, оның геометриялық көлеңке аймағына өтуіне әкеліп соғады. Жарық толқындарының геометриялық көлеңке аймағына өтіп кетуін Гюйгенс принципінің көмегімен түсірдіруге болады. Бұл принцип бойынша толқын барып жеткен әр нүкте екінші реттік толқын центрі болып табылады. Гюйгенс принципі толқын беттерін салудың таза геометриялық тәсілі бола тұра, толқын шебінің (фронтының) таралу бағытын ғана шешіп, әр бағытта таралатын толқындардың амплитудасы мен интенсивтігін анықтауды жүзеге асыра алмайды. Френель, Гюйгенс принципін екінші реттік толқын көздері идеясымен толықтырып, физикалық мағына берді. 6. Френельдің зоналар әдісі. Изотропты біртекті ортада S нүктелік жарық көзінен таралатын сфералық толқынның Р нүктесіне келіп түскен жарық тербелістерінің амплитудасын анықтайық (6.2-сурет). Мұндағы S толқын беттері Р түзуімен салыстырғанда симметриялы. Толқын бетін сақиналық аудандар - Френель зоналарына бөлейік, ол үшін центрі бір осьте жатқан шеңберлер жүргізейік. Шеңберлерден Р нүктесіне дейінгі қашықтықтарды бір-бірінен жарты толқын ұзындығына l/2-ге артық болатындай етіп салайық.
Сурет. Френель зоналары. Суретте көрсетілгендей, m-ші зонаның сыртқы шетінен Р нүктесіне дейінгі қашықтық bm мынадай: bm = b +ml/2, (6.3) мұндағы b − толқын бетінің О төбесінен Р нүктесіне дейінгі қашықтық. Екі көрші зонадан Р нүктесіне келіп жететін тербелістер қарама-қарсы фазада болады. Сондықтан да әр зонадан келіп түскен толқындардың көрші зонадан түскен толқындармен фаза айырымы p- ге тең болады. 7. Дөңгелек дискідегі және дөңгелек саңлаудағы Френель дифракциясы. Дөңгелек тесіктен алынатын дифракция. Сфералық толқынның жолына радиусы r0 дөңгелек тесік ойып алынған мөлдір емес экран қояйық.
6.4-сурет. Дөңгелек саңылаудағы жарық дифракциясы. 6.4а-суретте а − S жарық көзінен бөгетке дейінгі қашықтық, b − бөгеттен Р нүктесіне дейінгі қашықтық, мұнда r0<<a, b. Егер a мен b қашықтықтары мына қатынасты қанағаттандырса
мұндағы m - бүтін сан, онда тесік Р нүктесі үшін орнатылған m -ға тең алғашқы Френель зоналарын ашық қалдырады. Сондықтан, ашық Френель зоналарының саны мына өрнекпен анықталады: Р нүктесіндегі барлық зоналардан қозған қорытқы тербелістердің амплитудасы
болады, мұндағы плюс таңбасы тақ m-ға және минус таңбасы жұп m-ға сәйкес келеді. Кіші m-дер үшін амплитуда Еm мәні Е1 -ден аз ғана өзгеше болады. Тақ m-дерде Р нүктесіндегі амплитуда Е0=Е1, ал жұп m-дерде Е0=0 болады. Бөгетті алып тастағанда Р нүктесіндегі амплитуда Е0=Е1/2 болады. Сонымен, аз ғана тақ санды зоналарды ашатын бөгет амплитуданы екі есеге жуық, ал интенсивтікті - төрт есеге жуық арттырады. Сондықтан, дөңгелек тесіктен алынатын дифракциялық бейне центрі Р нүктесінде болатын кезектескен қара және жарық сақина түрінде болады (егер m жұп болса, центрде қара нүкте, ал m тақ болса ақ нүкте болады), интенсивтік максимумы бейне центрінен қашықтық бойынша азаяды (6.4 б,в-суреттерді қараңыз). Дөңгелек дискіден алынатын дифракция. Жарық көзі S пен бақылау нүктесі Р арасына радиусы r0 (6.5-сурет) мөлдір емес дөңгелек диск қояйық. Егер диск m алғашқы Френель зонасын жапса, Р нүктесіндегі амплитуда
болады. Жақша ішіндегі өрнектерді нөлге тең деп алуға болады, олай болса, Е0 = Еm+1 /2. (6.12) (6.12) өрнегі бойынша, дөңгелек мөлдір емес дискіден алынатын дифракцияда экранның центріндегі (Р нүктесіндегі) интенсивтік нөлден өзгеше болады.
Сонымен, дифракциялық бейне кезектескен жарық және қараңғы концентрлік сақиналар түрінде болады. Бейненің центрінде бірінші ашық Френель зонасының жартысына сәйкес келетін максимум болады (ақ дақ - Пуассон дағы). Максимумдер интенсивтігі бейне центрінен қашықтық бойынша азаяды (6.5 б-сурет). Дискінің радиусы өскен сайын бірінші ашық Френель зонасы Р нүктесінен алыстайды және осы зона бетіне нормаль мен Р нүктесіне бағыт арасындағы бұрыш ұлғаяды. Нәтижесінде орталық максимумның интенсивтігі диск мөлшері үлкейген сайын азаяды. Үлкен мөлшерлі дискіде оның арғы жағында көлеңке болады, оның шекарасы маңында өте нашар дифракциялық бейне орын алады. 8. Бір саңлаудағы Фраунгофер дифракциясы. Жазық монохромат жарық толқынының ені в саңылаудағы дифракциясын қарастырайық. Ұзындығы l жарық толқыны саңылау жазықтығына нормаль бағытта түссін (6.6-сурет). Параллель жарық шоғы мөлдір емес Э1 экрандағы саңылаудан өтіп, сәулелердің бастапқы түсу бағытының оң және сол жағына әртүрлі бұрыштармен дифракцияға түседі. Линза Л дифракцияға түскен параллель жарық шоқтарын, оның фокус жазықтығында орналасқан Э2 экранда жинайды. Дифракцияланбаған сәулелер В0 нүктесіне, ал дифракцияға түскен сәулелер j бұрышымен Вj нүктесіне жиналады. Саңылау жазықтығына параллель жарық шоғы нормаль түрде түскендіктен, толқын шебі (фронты) саңылау жазықтығымен бірдей болады, яғни саңылау жазықтығында толқын шебінің барлық нүктесі бірдей фазамен тербеледі. Саңылау жазықтығындағы толқын шебін саңылау шеттеріне параллель бірдей ені бар жолақтарға бөлейік. Әрбір жолақ екінші реттік жарық көзі болады. Экрандағы жарық амплитудаларын екі түрлі тәсілмен − графикалық және аналитикалық тәсілдермен шешуге болады.
6.6-сурет. Бір саңылаудағы Фраунгофер дифракциясы. 9. Дифракциялық тор. Қарапайым бір өлшемді дифракциялық тор деп ендері бірдей, біріне-біріне параллель, бір жазықтықта орналасқан өте көп N бірдей саңылаудан тұратын (олар бір-бірінен ені бірдей мөлдір емес жолақтармен бөлінген) жүйені айтады. Саңылау енін в, қара жолақ енін а деп белгілейік. d=а+в мәні дифракциялық тордың периоды деп аталады. Бір саңылаудан алынатын Фраунгофер дифракциясы сияқты, дифракция бұрышы бойынша дифракциялық тордың интенсивтігін графикалық және аналитикалық түрде өрнектеуге болады. Дифракциялық тордың интенсивтігінің бас максимум шарты төмендегі өрнекпен анықталады
мұндағы m − бас максимумдар реті. Нолдік ретті максимум біреу, 1 -ші, 2 -ші және т.б. ретті максимумдар екіден болады. 10. Нормаль (қалыпты) және аномаль (қалыпсыз) жарық дисперсиясы. Жарық дисперсиясының электр |



 (2.26)
(2.26) таралған болады. Сонымен,
таралған болады. Сонымен, . (2.27)
. (2.27) (2.9)
(2.9) – магнетиктің магнит моменті, ол сан жағынан жеке молекулалардың магнит моменттерінің қосындысына тең.
– магнетиктің магнит моменті, ол сан жағынан жеке молекулалардың магнит моменттерінің қосындысына тең. , яғни вакуум үшін χ =0. Вакуум үшін m=1 болғандықтан, магнит тұрақтысы m0 вакуумның магнит өтімділігі деп аталады. Магнит сезімталдылығы χ <0 және абсолют шамасы жағынан аз магнетиктер диамагнетиктер деп аталады. Диамагнетиктер үшін m<1. Магнит сезімталдылығы χ>0 (m>1) және шама жағынан аз болатын магнетиктер парамагнетиктер деп аталады. Ферромагнетиктер, олар үшін χ >0 және өте үлкен мәнге ие бола алады.
, яғни вакуум үшін χ =0. Вакуум үшін m=1 болғандықтан, магнит тұрақтысы m0 вакуумның магнит өтімділігі деп аталады. Магнит сезімталдылығы χ <0 және абсолют шамасы жағынан аз магнетиктер диамагнетиктер деп аталады. Диамагнетиктер үшін m<1. Магнит сезімталдылығы χ>0 (m>1) және шама жағынан аз болатын магнетиктер парамагнетиктер деп аталады. Ферромагнетиктер, олар үшін χ >0 және өте үлкен мәнге ие бола алады.
 .
.



 және магнит индукция векторы
және магнит индукция векторы 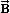 арқылы сипатталатыны белгiлi. Олай болса, электромагниттiк өрiс тарап жатқан кеңiстiктiң әрбiр нүктесiнде осы векторлардың мәнi периодты түрде өзгерiп отырады. Электромагниттiк толқындар – көлденең толқындар.
арқылы сипатталатыны белгiлi. Олай болса, электромагниттiк өрiс тарап жатқан кеңiстiктiң әрбiр нүктесiнде осы векторлардың мәнi периодты түрде өзгерiп отырады. Электромагниттiк толқындар – көлденең толқындар. 
 , (3.30)
, (3.30) және
және  векторларының тербелу жиіліктері мен фазаларының бірдей болатындығын көрсетеді, яғни олардың максимал және минимал шамаларына бірдей уақытта жетіп отыратындығын айқындайды.
векторларының тербелу жиіліктері мен фазаларының бірдей болатындығын көрсетеді, яғни олардың максимал және минимал шамаларына бірдей уақытта жетіп отыратындығын айқындайды. (3.31)
(3.31) (1.23)
(1.23)
 конденсатордағы кернеу;
конденсатордағы кернеу; катушкадан айнымалы ток өткендегі өздік индукция эқк.
катушкадан айнымалы ток өткендегі өздік индукция эқк.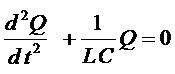 (201)
(201)
 конденсатордағы заряд тербелістерінің амплитудасы
конденсатордағы заряд тербелістерінің амплитудасы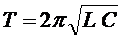
 . (206)
. (206) өшу коэффициенті.
өшу коэффициенті. . (207)
. (207) ) өшетін тербелістің периоды ұғымын көршілес екі максимум-ның немесе минимумның орындалатын уақыт аралығы ретінде шартты түрде қолдану қажет.
) өшетін тербелістің периоды ұғымын көршілес екі максимум-ның немесе минимумның орындалатын уақыт аралығы ретінде шартты түрде қолдану қажет.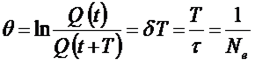 . (210)
. (210) - тербелістің амплитудасы есе кемитін уақыт аралығындағы (релаксация уақытындағы) тербеліс саны. өшудің логарифмдік декременті – берілген тербеліс жүйесі үшін тұрақты шама.
- тербелістің амплитудасы есе кемитін уақыт аралығындағы (релаксация уақытындағы) тербеліс саны. өшудің логарифмдік декременті – берілген тербеліс жүйесі үшін тұрақты шама. эқк-нің ықпалымен орындалатын өшпейтін тербелістер (
эқк-нің ықпалымен орындалатын өшпейтін тербелістер (  – эқк-нің амплитудалық мәні,
– эқк-нің амплитудалық мәні,  – сыртқы эқк-нің жиілігі).
– сыртқы эқк-нің жиілігі).
 катушкадан, сыйымдылығы
катушкадан, сыйымдылығы  конденсатордан және кедергісі резистордан тұратын тізбектің қысқыштарына
конденсатордан және кедергісі резистордан тұратын тізбектің қысқыштарына 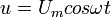 айнымалы кернеу түсірейік (2.15-сурет). Ток күшінің
айнымалы кернеу түсірейік (2.15-сурет). Ток күшінің  лездік мәні де, амплитудалық мәні де тізбектей жалғанған тізбектің барлық бөлігінде бірдей болады. Ал ток көзінің полюстеріндегі лездік кернеу оның жеке бөліктеріндегі кернеудің лездік мәндерінің қосындысына тең:
лездік мәні де, амплитудалық мәні де тізбектей жалғанған тізбектің барлық бөлігінде бірдей болады. Ал ток көзінің полюстеріндегі лездік кернеу оның жеке бөліктеріндегі кернеудің лездік мәндерінің қосындысына тең: (2.14)
(2.14)
 аламыз.
аламыз. онда
онда 
 (2.18)
(2.18) және
және 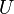 деп белгілесек,
деп белгілесек, (2.19)
(2.19) шамасы қуат коэффициенті деп аталады. Осы өрнек айнымалы токтың қуаты тек ток күші мен кернеуге ғана емес, сонымен қатар олардың тербеліс фазаларының айырымына да тәуелді екенін көрсетеді.
шамасы қуат коэффициенті деп аталады. Осы өрнек айнымалы токтың қуаты тек ток күші мен кернеуге ғана емес, сонымен қатар олардың тербеліс фазаларының айырымына да тәуелді екенін көрсетеді. , (4.2)
, (4.2)
 Жарық тығыздығы үлкен ортадан тығыздығы кіші ортаға өткенде пайда болады.
Жарық тығыздығы үлкен ортадан тығыздығы кіші ортаға өткенде пайда болады.

















 (Вт)
(Вт) = 0,40 мкм-ден кем және 0,76 мкм-ден артық электромагнитті толқындар көзге көрінбейді.
= 0,40 мкм-ден кем және 0,76 мкм-ден артық электромагнитті толқындар көзге көрінбейді. жарық ағынының бұл беттің
жарық ағынының бұл беттің  ауданының қатынасына тең шаманы айтады:
ауданының қатынасына тең шаманы айтады: . (4.16)
. (4.16) .
. , жарық көзінен жарық сәулесі түсетін бетке дейінгі қашықтықпен
, жарық көзінен жарық сәулесі түсетін бетке дейінгі қашықтықпен  және
және  бұрышы арқылы өрнектеуге болады:
бұрышы арқылы өрнектеуге болады: , (4.17)
, (4.17) және
және 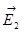 . Суперпозиция принципі бойынша өрістің қортқы кернеулігі мынаған тең болады
. Суперпозиция принципі бойынша өрістің қортқы кернеулігі мынаған тең болады ,
,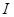 ~
~  ,
, , (5.1)
, (5.1) −
−  , мұндағы α − олардың арасындағы бұрыш. Когерентті толқындарды тек жасанды әдіспен алу мүмкін: ол үшін жеке атом шығаратын толқынды қандай да бір оптикалық құралмен екі немесе одан да көп бөліктерге жіктеу қажет, содан соң, берілген Р нүктесінде оларды қосудың нәтижелерін бақылау керек. Осы кезде бір толқынның жеке бөліктері өзара когерентті болады. Егер бұл толқындар әртүрлі жол
, мұндағы α − олардың арасындағы бұрыш. Когерентті толқындарды тек жасанды әдіспен алу мүмкін: ол үшін жеке атом шығаратын толқынды қандай да бір оптикалық құралмен екі немесе одан да көп бөліктерге жіктеу қажет, содан соң, берілген Р нүктесінде оларды қосудың нәтижелерін бақылау керек. Осы кезде бір толқынның жеке бөліктері өзара когерентті болады. Егер бұл толқындар әртүрлі жол  жүрсе (шығу нүктесінен бастап олардың қосылу нүктесіне дейінгі аралықта), онда олардың арасында фаза айырымы болады. Сонымен, біз екі тербелістің қосылуын қарастыралық
жүрсе (шығу нүктесінен бастап олардың қосылу нүктесіне дейінгі аралықта), онда олардың арасында фаза айырымы болады. Сонымен, біз екі тербелістің қосылуын қарастыралық , (5.2)
, (5.2) және
және  , толқындық векторлар әртүрлі болады:
, толқындық векторлар әртүрлі болады:  және
және  , өйткені бұл екі толқын
, өйткені бұл екі толқын  және
және 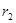 жол жүруі мүмкін. Олардың сыну көрсеткіштері
жол жүруі мүмкін. Олардың сыну көрсеткіштері  ,
,  . Онда бұл когерентті толқындардың фаза айырымы
. Онда бұл когерентті толқындардың фаза айырымы , (5.3)
, (5.3) − вакуумдағы толқын ұзындығы,
− вакуумдағы толқын ұзындығы,  − жарық толқынының оптикалық жол айырымы. Сонымен, фаза айырымы мен оптикалық жол айырымы арасындағы байланыс:
− жарық толқынының оптикалық жол айырымы. Сонымен, фаза айырымы мен оптикалық жол айырымы арасындағы байланыс: . (5.4)
. (5.4)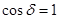 мәні кезінде байқалады, демек
мәні кезінде байқалады, демек  үшін (m=0,1,2, ...)
үшін (m=0,1,2, ...) ,
, . (5 5)
. (5 5) мәні кезінде байқалады, демек
мәні кезінде байқалады, демек ,
, ,
, . (5.6)
. (5.6)
 және жиілігі
және жиілігі  интервалында жататын тербелістердің жиынтығы болады. Олай болса, Е қорытқы өрістің кернеулігі периодты функциямен сипатталатын айнымалы шама – квази - монохромат толқын болады.
интервалында жататын тербелістердің жиынтығы болады. Олай болса, Е қорытқы өрістің кернеулігі периодты функциямен сипатталатын айнымалы шама – квази - монохромат толқын болады.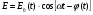 . (5.7)
. (5.7) мен фазасы
мен фазасы  тұрақты болатын ең аз уақыт интервалын
тұрақты болатын ең аз уақыт интервалын  деп алайық. Бұл уақыт интервалы
деп алайық. Бұл уақыт интервалы  радианға ауысып үлгереді (қарсы фазаға). Қарапайым жарық көздері үшін оның шамасы 10-9¸10-10с, ал лазер сәулесі шамамен 10-3с.
радианға ауысып үлгереді (қарсы фазаға). Қарапайым жарық көздері үшін оның шамасы 10-9¸10-10с, ал лазер сәулесі шамамен 10-3с. . (5.8)
. (5.8) ког
ког ~
~  және жолақ номері өскен сайын жол айырымы да өседі, сондықтан жолақ бұлыңғыр тартады. Экран ортасы үшін
және жолақ номері өскен сайын жол айырымы да өседі, сондықтан жолақ бұлыңғыр тартады. Экран ортасы үшін  , (5.9)
, (5.9) жиілік интервалы неғұрлым үлкен болса, жарықтың уақыттық когерентігі соғұрлым аз болатынын байқаймыз.
жиілік интервалы неғұрлым үлкен болса, жарықтың уақыттық когерентігі соғұрлым аз болатынын байқаймыз. , (5.11)
, (5.11) , (5.16)
, (5.16) =0,5 мкм,
=0,5 мкм,  =0,2·10-2 мкм – адам көзінің екі толқынды бір нәрсе ретінде қабылдау кезіндегі минимал интервал. Есептеулер l-дің мәні үшін
=0,2·10-2 мкм – адам көзінің екі толқынды бір нәрсе ретінде қабылдау кезіндегі минимал интервал. Есептеулер l-дің мәні үшін  0,06мм-ді береді, сонымен, жұқа пластинкадан шағылған жарық сәулесі кезіндегі интерференцияның байқалуы былай болады: l пластинка қалыңдығының артуына байланысты max және mіn жақындайды, сөйтіп интерференциялық бейне жойылады. n мен l (монохроматтық жарық) -ның берілген мәндері кезінде, қалыңдығы l тұрақты пластинкаға a түсу бұрышының әрбір мәніне өзінің интерференциялық жолағы (яғни max және mіn) сәйкес келеді. Бұл интерференциялық бейне бірдей көлбеуліктегі жолақ деп аталады.
0,06мм-ді береді, сонымен, жұқа пластинкадан шағылған жарық сәулесі кезіндегі интерференцияның байқалуы былай болады: l пластинка қалыңдығының артуына байланысты max және mіn жақындайды, сөйтіп интерференциялық бейне жойылады. n мен l (монохроматтық жарық) -ның берілген мәндері кезінде, қалыңдығы l тұрақты пластинкаға a түсу бұрышының әрбір мәніне өзінің интерференциялық жолағы (яғни max және mіn) сәйкес келеді. Бұл интерференциялық бейне бірдей көлбеуліктегі жолақ деп аталады.

 , (6.9)
, (6.9)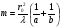 . (6.10)
. (6.10) (6.11)
(6.11)


 , (m=0,1,2,3,...) (6.16)
, (m=0,1,2,3,...) (6.16)