 ПОЗНАВАТЕЛЬНОЕ
| Изменение матрицы линейного преобразования при изменении базиса 12
В предыдущем разделе мы установили, что как только в линейном пространстве выбран базис, то каждому линейному преобразованию соответствует матрица этого преобразования. Однако если выбрать в пространстве другой базис, то матрица преобразования, как правило, станет другой. Выясним, как эти матрицы связаны между собой. Пусть Предложение 19.1 Пусть
Доказательство. Пусть Определение 19.2 Две квадратных матрицы Следствие 19.1 Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах. Напомним, что в евклидовом пространстве определено скалярное произведение векторов Определение. Если существует такой оператор B, что для любых Теорема. Если A — линейный оператор в евклидовом пространстве E и A — его матрица в некотором ортонормированном базисе в E, то у оператора есть единственный сопряженный оператор, причем матрица сопряженного оператора в том же базисе — это матрица AT. Теорема доказана на лекции. Пример. Рассмотрим оператор Uj поворота пространства R2 на угол j относительно начала координат против часовой стрелки:
Матрицы операторов поворота на угол j и угол - j имеют, соответственно, вид:
Нетрудно доказать (на лекции доказано) следующие свойства сопряженного оператора: · что сопряженный к линейному оператру — линейный оператор; · · · · характеристические многочлены операторов совпадают. 5.3.2. Самосопряженный оператор Определение. Если линейный оператор A, действующий в евклидовом пространсте E, таков, что для любых Пример. Оператор P2 — оператор проектирования пространства R3 на подпространство R2 параллельно вектору Как показано выше, матрица оператора P2 в естественном ортонормированном базисе Имеет вид
Тогда
Видно, что матрица P2 оператора P2 — симметричная матрица. Нетрудно доказать следующие свойства самосопряженного оператора: · сумма самосопряженных операторов — самосопряженный оператор; · если оператор A самосопряженный оператор, то оператор 31. Собственные значения и собственные векторы самосопряженного оператора Можно показать (на лекции не доказывается), что у самосопряженного оператора существует собственный ортонормированный базис. Поскольку A=A*, то матрица самосопряженного оператора — симметричная матрица. Справедлива следующая теорема. Теорема. Матрица самосопряженного оператора в собственном базисе имеет диагональную форму. Ясно, что для того чтобы привести матрицу самосопряженного оператор к диагональному виду нужно найти собственные значения оператора и диагональную матрицу, на диагонали которой расположены собственные значения матрицы. Если нужно записать выражение для приведения матрицы к этой диагональной форме, то нужно еще найти собственные векторы матрицы, записать матрицу C перехода к собственному базису (матрицу, столбцами которой являются координаты собственных векторов оператора), найти обратную к ней матрицу С-1 и тогда 32 Характеристический многочлен линейного оператора
Рассмотрим конечномерное векторное пространство над полем . Зафиксируем на нем линейный оператор . Через будем обозначать матрицу оператора в некотором заранее выбранном базисе. Инвариантные подпространства
Определение 1. Подпространство называется инвариантным1) относительно линейного оператора , если .
Теорема 1. Пространство является прямой суммой двух подпространств и , инвариантных относительно линейного оператора , тогда и только тогда, когда в некотором базисе матрица оператора имеет клеточно-диагональный вид:
12 |
 --
--  -мерное линейное пространство,
-мерное линейное пространство,  и
и  -- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть
-- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть  -- матрица перехода 19.1.4 а от старого базиса к новому.
-- матрица перехода 19.1.4 а от старого базиса к новому. -- линейное преобразование пространства
-- линейное преобразование пространства  и
и  -- матрицы этого преобразования в старом и новом базисе соответственно. Тогда
-- матрицы этого преобразования в старом и новом базисе соответственно. Тогда
 -- произвольный вектор пространства
-- произвольный вектор пространства 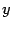 -- его образ, то есть
-- его образ, то есть  . Пусть
. Пусть  и
и  -- координатные столбцы векторов
-- координатные столбцы векторов  ,
, 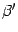 -- в новом. Тогда в силу формулы (19.3)
-- в новом. Тогда в силу формулы (19.3)  . По предложению 18.5 имеем
. По предложению 18.5 имеем  ,
, 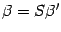 . Подставим эти выражения в предыдущую формулу, получаем
. Подставим эти выражения в предыдущую формулу, получаем  . Откуда
. Откуда  . С другой стороны, в силу формулы (19.3) в новом базисе
. С другой стороны, в силу формулы (19.3) в новом базисе  . Сравнивая это равенство с предыдущим, получаем
. Сравнивая это равенство с предыдущим, получаем  .
. и
и  одного порядка называются подобными, если существует такая невырожденная матрица
одного порядка называются подобными, если существует такая невырожденная матрица  .
.
 и
и  из евклидова пространства E справедливо
из евклидова пространства E справедливо  , то оператор B называется сопряженным оператором к оператору A и обозначается A*:
, то оператор B называется сопряженным оператором к оператору A и обозначается A*: 

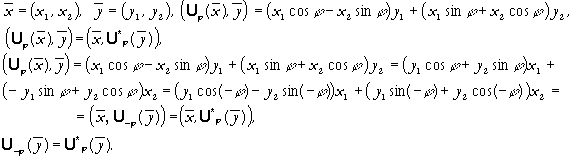
 Видно, что
Видно, что 



 и
и 
 , то оператор A называется самосопряженным оператором.
, то оператор A называется самосопряженным оператором.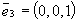 :
:  .
.

 т.е.
т.е.  — оператор P2 — самосопряженный оператор.
— оператор P2 — самосопряженный оператор. — тоже самосопряженный оператор (
— тоже самосопряженный оператор (  — действительное число).
— действительное число). — равенство, связывающее диагональну форму
— равенство, связывающее диагональну форму  матрицы оператора в собственном базисе с матрицей A оператора в заданном базисе.
матрицы оператора в собственном базисе с матрицей A оператора в заданном базисе.