 ПОЗНАВАТЕЛЬНОЕ
| ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Лабораторная работа №3
ИЗУЧЕНИЕ УПРУГОГО УДАРА ТВЕРДЫХ ТЕЛ ЦЕЛЬ РАБОТЫ Определение коэффициента восстановления относительной скорости и необратимых потерь кинетической энергии при прямом центральном упругом ударе двух шаров.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Предварительно необходимо изучить теоретические основы работы № 2. Ударом твердых тел называется совокупность явлений, возникающих при столкновении движущихся твердых тел. Время удара t очень мало, составляет примерно
Линией удара MN называется общая нормаль к поверхностям соударяющихся тел в точке соприкосновения К (рис.6). Если центры масс С1 и С2 тел лежат на линии удара, то удар называется центральным, а если не лежат, то - нецентральным. Если скорости v1 и v2 центров масс тел в начале удара параллельны линии удара, то удар называется прямым, в противном случае - косым. Уравнения законов сохранения импульса и энергии, справедливых для абсолютно упругого удара, имеют вид :
где Решая эту систему для прямого центрального удара шаров, получим :
т.е. относительная скорость тел при абсолютно упругом прямом центральном ударе сохраняется по модулю, меняя свое направление на противоположное. При реальном прямом центральном ударе вместо уравнения (3) получим :
где k - коэффициент восстановления относительной скорости. При абсолютно упругом ударе k = 1; при абсолютно неупругом ударе k = 0; для упругих ударов реальных тел 1 > k > 0. В частности, при столкновении тел из дерева Решая совместно систему уравнений (1) и (4) для прямого центрального удара шаров, получим :
Отсюда легко определить величину необратимых потерь кинетической энергии при ударе :
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ Экспериментальная установка представляет собой платформу 3 с вертикальной стойкой 4 (см.рис.7), на вершине которой закреплены нити с подвешенными шарами 1 и 2. На платформе расположены две круговые шкалы 5, электромагнит 6 и кнопка пуска 7. Винты 8 регулируют положение шаров так, чтобы в положении равновесия их центры находились на одной высоте, а поверхности соприкасались. Шар 1 с меньшей массой отклоняют от положения равновесия так, что
нить
подвеса шара образует с вертикалью угол g. При этом центр шара поднимается от положения равновесия на высоту H = L - Lcosg = L(1 - cosg), где L - расстояние от точки подвеса до центра шара. Если из этого положения шар отпустить, то он начинает двигаться в положение равновесия и перед ударом со вторым шаром приобретает скорость v1 , которую найдем, применяя закон сохранения энергии для движения первого шара и пренебрегая сопротивлением движению :
отсюда После прямого центрального удара первый и второй шары получают скорости u1 и u2 . Двигаясь свободно, шары отклоняются от своих положений равновесия так, что направления нитей подвеса образуют углы a и b с вертикалью, а шары поднимаются на высоты h1 и h2 , причем h1 = L - Lcosa = L(1 - cosa) = 2Lsin2(a/2) , h2 = L - Lcosb = L(1 - cosb) = 2Lsin2(b/2) . (9) Пренебрегая сопротивлением движению шаров после удара, по закону сохранения энергии получим :
Шар с большей массой m2 перед ударом покоится, т.е. v2 = 0. Если шары после удара движутся в одном направлении, то с учетом формул (4), (8), (10) и (11) коэффициент восстановления относительной скорости шаров равен
Если шары после удара движутся в разные стороны, то направления векторов u1 и u2 противоположны, т.е.
В частном случае при g = 900 формула (13) принимает вид :
Необратимая потеря кинетической энергии dЕ при прямом центральном ударе шаров равна dE = m1v12/2 - m1u12/2 - m2u22/2 = = 2m1gLsin2(g/2) - 2m1gLsin2(a/2) - 2m2gLsin2(b/2) = =2gL[m1sin2(g/2) - m1sin2(a/2) - m2sin2(b/2)] . (14) С учетом формулы (7) dE можно определить так :
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВОССТАНОВЛЕНИЯ ОТНОСИТЕЛЬНОЙ СКОРОСТИ 1. С помощью винтов 8 (см.рис.7) отрегулируйте экспериментальную установку так, чтобы в положении равновесия шары касались друг друга, а их удар был прямым и центральным. Включите установку нажатием кнопки "СЕТЬ". 2. Найдите массы шаров m1 и m2 и запишите их в таблицу 1. 3. Измерьте штангенциркулем диаметры шаров d1 и d2 и линейкой длину нитей R1 и R2 от точек подвеса до поверхности шаров. 4. По формулам L1 = R1 + d1/2 и L2 = R2 + d2/2 найдите расстояния L1 и L2 от точек подвеса нитей до центров шаров. Если результаты вычислений отличаются друг от друга более чем на 1 мм, то подъемом или опусканием одного из шаров сравняйте длины L1 и L2 . Тогда L1 = L2 = L. Результат измерения L запишите в таблицу. 5. Включите электромагнит нажатием кнопки ²ВКЛ². Поместите шар с меньшей массой m1 в гнездо электромагнита и измерьте угол g отклонения нити подвеса этого шара от вертикали. Убедившись в неподвижности другого шара, отпустите легкий шар нажатием кнопки ²ПУСК². Наблюдая прямой центральный удар шаров, измерьте и запишите в таблицу углы максимального отклонения a и b нитей подвеса шаров от вертикали после удара. Проведите наблюдения углов a, b, g не менее 5 раз. 6. Результаты измерения Таблица 1
7. Подставляя результаты измерения 8. Полуширину доверительного интервала Dk найдите по формуле :
где Da, Db, Dg - полуширины доверительных интервалов углов a, b, g, измеренные в радианах. 9. Результат измерения запишите в виде доверительного интервала : k ± Dk.
Упражнение 2. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ НЕОБРАТИМЫХ ПОТЕРЬ КИНЕТИЧЕСКОЙ ЭНЕРГИИ 10. Используя результаты измерения 11. Пренебрегая ошибками измерения длины подвеса шаров L, ускорения свободного падения g и масс шаров m1 и m2 , найдите полуширину доверительного интервала D(dЕ) по формуле :
Результат измерения запишите в виде : dЕ ± D(dЕ). 12. Оцените величину dЕ по формуле (15) и сравните с результатом, полученным в пункте 11.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте цель лабораторной работы. 2. Укажите явления, происходящие при упругом ударе твердых тел. 3. Оцените время удара твердых тел. 4. По какой формуле можно найти импульс ударной силы ? 5. Сформулируйте законы сохранения импульса и механической энергии 6. Какой удар называется абсолютно упругим ? 7. Какой удар называется абсолютно неупругим ? 8. Сохраняется ли механическая энергия соударяющихся тел при реальном упругом ударе ? 9. Какой удар тел называется центральным ? 10. Какой удар называется: 1) прямым; 2) косым ? 11. Какую величину называют коэффициентом восстановления относительной скорости? 12. Чему равен коэффициент восстановления относительной скорости при абсолютно упругом ударе твердых тел ?
13. Укажите величину коэффициента восстановления относительной скорости тел при абсолютно неупругом ударе. 14. В каких пределах меняется величина коэффициента восстановления относительной скорости тел при реальном упругом ударе? 15. Напишите систему уравнений, решая которую можно найти скорости шаров после абсолютно упругого удара. 16. Какие скорости имеют шары равной массы после абсолютно упругого прямого центрального удара ? 17. Какие уравнения образуют систему, решая которую можно найти скорости шаров после реального упругого удара ? 18. Нарисуйте эскиз экспериментальной установки. 19. Какую величину определяют при выполнении упражнения 1 ? 20. Укажите порядок выполнения упражнения 1 21. По какой формуле получают значение угла в радианах ? 22. Как высота подъема шара от положения равновесия связана с углом отклонения нити (стержня) подвеса от вертикали ? 23. Как при выполнении данной работы находят скорости шаров до и после удара? 24. По какой формуле определяют коэффициент восстановления относительной скорости шаров, если после удара шары движутся в разные стороны? 25. По какой формуле вычисляют полуширину Dk доверительного интервала коэффициента восстановления относительной скорости шаров ? 26. Какую величину определяют в упражнении 2 ? 27. Выполняется ли для кратковременного реального упругого удара закон сохранения импульса ? 28. Укажите формулу для определения величины необратимых потерь кинетической энергии. 29. Укажите формулу для вычисления полуширины доверительного интервала величины необратимых потерь кинетической энергии. 30. Что происходит с механической энергией шаров при реальном упругом ударе?
|



 с. Процесс упругого столкновения двух тел можно разделить на две фазы. В первой фазе, которая начинается в момент соприкосновения тел, кинетическая энергия соударяющихся тел переходит в потенциальную энергию деформации. Первая фаза заканчивается прекращением сближения тел. Во второй фазе упругого удара тела расходятся, и потенциальная энергия упругой деформации тел переходит в их кинетическую энергию.
с. Процесс упругого столкновения двух тел можно разделить на две фазы. В первой фазе, которая начинается в момент соприкосновения тел, кинетическая энергия соударяющихся тел переходит в потенциальную энергию деформации. Первая фаза заканчивается прекращением сближения тел. Во второй фазе упругого удара тела расходятся, и потенциальная энергия упругой деформации тел переходит в их кинетическую энергию. Абсолютно упругим ударом называется такой удар, при котором сохраняется полная механическая энергия соударяющихся тел. При реальном упругом ударе часть механической энергии тел переходит в другие виды энергии (внутреннюю энергию, энергию звуковых волн и т.д.), т.е. появляется необратимая потеря механической энергии dЕ . Абсолютно неупругим ударом называется удар, после которого скорости тел одинаковы.
Абсолютно упругим ударом называется такой удар, при котором сохраняется полная механическая энергия соударяющихся тел. При реальном упругом ударе часть механической энергии тел переходит в другие виды энергии (внутреннюю энергию, энергию звуковых волн и т.д.), т.е. появляется необратимая потеря механической энергии dЕ . Абсолютно неупругим ударом называется удар, после которого скорости тел одинаковы. , (1)
, (1) , (2)
, (2) - скорости тел после удара.
- скорости тел после удара. , (3)
, (3)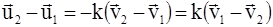 , (4)
, (4)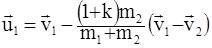 , (5)
, (5) . (6)
. (6) . (7)
. (7)
 ,
, . (8)
. (8) ;
; . (10)
. (10) ;
; . (11)
. (11) . (12)
. (12) , и коэффициент восстановления относительной скорости шаров определяется по формуле :
, и коэффициент восстановления относительной скорости шаров определяется по формуле : . (13)
. (13) . (13¢)
. (13¢) . (15)
. (15) ,
,  ,
,  углов отклонения вычислите по формуле (1.1) главы I. Выборочные оценки S(
углов отклонения вычислите по формуле (1.1) главы I. Выборочные оценки S( 
 ,
, . (16)
. (16)