 ПОЗНАВАТЕЛЬНОЕ
| ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Лабораторная работа №2 ИЗУЧЕНИЕ АБСОЛЮТНО НЕУПРУГОГО УДАРА
ЦЕЛЬ РАБОТЫ
Изучение абсолютно неупругого удара. Оценка действующих сил и величины необратимых потерь механической энергии при абсолютно неупругом ударе. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Материальной точкой называется тело, размеры которого много меньше масштаба движения. В дальнейшем в этом пункте под словом "тело" следует подразумевать материальную точку. Силы, действующие на тела механической системы, можно разделить на две группы: 1) внешние силы 2) внутренние силы
Система тел называется изолированной или замкнутой, если на тела системы не действуют внешние силы, т.е. Если ускорение
где Рассмотрим систему двух тел с массами m1 и m2. Пусть тела системы взаимодействуют с силами
Складывая уравнения (3) и (4) и учитывая равенство (1), получим
Из уравнения (5) следует закон сохранения импульса: если система является изолированной (
Изменение скорости
где Импульсами внешних сил, например, сил тяжести, а также перемещениями тел за малое время удара Dt можно пренебречь. В этом случае уравнения (3) и (4) принимают вид:
Складывая уравнения (3¢) и (4¢) с учетом (1), получим уравнение (6), т.е. при кратковременных взаимодействиях даже в неизолированных системах закон сохранения импульса приближенно выполняется. Удар называется абсолютно неупругим, если после удара скорости тел одинаковы:
Изменение кинетической энергии тел при абсолютно неупругом ударе равно
Для кратковременного удара изменениями положения тел и их потенциальной энергии Ер можно пренебречь: DЕр = 0. Так как DЕk < 0, то полная механическая энергия тел убывает, переходя в другие виды энергии. Удар, при котором полная механическая энергия тел сохраняется, называется абсолютно упругим. Закон сохранения механической энергии можно сформулировать так: полная механическая энергия системы тел сохраняется, если система изолирована и на тела системы не действуют внутренние диссипативные силы (например, силы трения).
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
После удара свая движется в разрезной втулке 3, действующей на сваю силой трения скольжения. Поэтому после удара груз и свая движутся замедленно до полной остановки. Меняя положение гири 5, скользящей по рычагу 4, можно менять силу нормального давления втулки на сваю, а значит, менять силу трения. Рычаг 4 может поворачиваться относительно горизонтальной оси О. Для предварительного закрепления груза 1 на некоторой высоте служит защелка 6, положение которой на нужной высоте фиксируется стопорными винтами. Груз поднимают вверх до соприкосновения с защелкой. Чтобы освободить груз, нужно нажать на ручку 7 защелки. Положение груза и сваи до и после удара определяется с помощью их указателей по вертикальной шкале 8. Экспериментальная установка находится внутри металлического кожуха 9. При почти свободном падении с высоты Н груз приобретает скорость v1, которую находим по кинематической формуле
учитывая начальную скорость v0 = 0. Для абсолютно неупругого кратковременного удара груза и сваи можно приближенно применить закон сохранения импульса (6) и найти общую скорость груза и сваи после удара. Так как до удара свая покоилась (v2 = 0), а скорость груза равна v1, то скорость u после удара равна
При ударе между грузом и сваей возникают ударные силы Отсюда
Подставляя (9) и (8) в формулу (10), получим
Так как время удара Dt » 2×10-4 с очень мало, то внутренняя сила f, действующая на груз, много больше внешней силы тяжести Учитывая, что до удара свая покоилась (v2 = 0), полная механическая энергия системы "груз-свая" согласно формуле (7) уменьшается на величину
Если эту величину необратимых потерь механической энергии поделить на начальную энергию
Поделив числитель и знаменатель формулы (13) на m2, получим
Из формулы (13¢) видно, что доля необратимых потерь энергии при ударе груза и сваи уменьшается с увеличением отношения При ударе груза и сваи соприкасаются нижняя поверхность груза и верхняя поверхность сваи. В первую очередь нас будет интересовать изменение положения этих поверхностей. На рис.5 груз 1 до падения и свая 2 в начальном положении показаны пунктиром, а в конечном положении после удара и замедленного движения - сплошной линией. Расстояния Н1, h1, h2 измеряют по вертикальной линейке 8 (рис.4) и записывают в таблицу 1. На рис.5 видно, что высота падения груза
а путь S замедленного движения груза и сваи до остановки
Работа усредненной силы трения
равна изменению полной механической энергии этих тел
Отсюда, с учетом формул (9) и (8), усредненная сила трения равна
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. ОПРЕДЕЛЕНИЕ СРЕДНЕЙ СИЛЫ ТРЕНИЯ
1. Поместите гирю 5 (см.рис.4) на сравнительно небольшом расстоянии L1 от оси вращения О рычага 4. 2. Поднимите сваю 2 на максимальную высоту. 3. С помощью защелки 6 расположите груз 1 на такой высоте Н1, чтобы после удара с грузом свая не касалась втулки 3 своей горизонтальной платформой. 4. По вертикальной линейке 8 измерьте положение Н1 указателя груза и положение h1 указателя сваи до удара. Результаты измерения занесите в таблицу 1. 5. Нажимая на защелку 7, освободите груз. Наблюдайте абсолютно неупругий удар груза и сваи, а также их замедленное движение после удара. Измерьте положение h2 указателя сваи после удара и результат измерения запишите в таблицу 1. 6. Повторите пункты 2¸5 еще четыре раза при тех же значениях Н1 и h1. 7. Передвиньте гирю 5 вдоль рычага 4 на новое расстояние L2 от оси вращения О, установив гирю в середине рычага. Измените высоту Н1 поднятия груза. При изменении высоты Н1 поднятия груза необходимо контролировать выполнение пункта 3. Повторите измерения, указанные в пунктах 2 ¸ 6, при новом расстоянии L2. 8. Передвиньте гирю 5 на максимальное расстояние L3 от оси вращения О и повторите измерения, указанные в пунктах 2 ¸ 6. 9. Используя методику обработки результатов прямых измерений, изложенную в главе I, для каждого L найдите средние значения величин Н1, h1, h2 и полуширину доверительных интервалов DН1, Dh1, Dh2. 10. Для каждого L по формулам (14) и (15) найдите высоту Н падения груза и путь S замедленного движения тел после удара, а по формулам
определите полуширину доверительных интервалов этих величин. 11. Для каждого L по формуле (17) вычислите усредненную силу трения F, используя данные экспериментальной установки: m1 = 0,32 кг; m2 = 0,12 кг; Dm1 = Dm2 = Dm = 1 г = 0,001 кг. Пренебрегая погрешностью Dg ускорения свободного падения, полуширину доверительного интервала DF найдите по формуле:
Таблица 1
Результаты вычислений занесите в таблицу 1. Сравните силу трения F для разных значений L длины рычага, т.е. для разных величин силы нормального давления.
Упражнение 2. ОЦЕНКА ВЕЛИЧИНЫ 12. По формуле (11) оцените величину внутренней силы f, действующей на груз при абсолютно неупругом ударе груза и сваи, считая, что время удара Dt » 2×10-4 с. Сравните полученную силу с силой тяжести FТ = m1g, которая является внешней силой в системе "груз-свая".
Упражнение 3. ОПРЕДЕЛЕНИЕ НЕОБРАТИМЫХ ПОТЕРЬ
13. Подставляя формулу (8) в формулу (12), получим расчетную формулу для величины необратимых потерь механической энергии при абсолютно неупругом ударе груза и сваи:
Найдите величину необратимых потерь механической энергии dЕ, а полуширину доверительного интервала D(dЕ) этой величины определите с помощью формулы:
14. Долю g необратимых потерь механической энергии определите по формуле (13), а полуширину доверительного интервала Dg найдите с помощью формулы:
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Сформулируйте цель лабораторной работы 2. Сформулируйте закон сохранения импульса 3. Какой удар называется абсолютно упругим? 4. Какой удар называется абсолютно неупругим? 5. Что происходит с механической энергией при абсолютно неупругом ударе? 6. Выполняется ли закон сохранения импульса при кратковременном абсолютно неупругом ударе? 7. Какую скорость имеет груз после свободного падения с высоты Н = 1 м? 8. Какую скорость имел груз до удара о сваю, если после абсолютно неупругого удара скорость груза и сваи равна 2,4 м/с, а масса сваи в 3 раза меньше массы груза? 9. Выполняется ли закон сохранения механической энергии при свободном падении груза до удара? 10. Как движутся груз и свая после абсолютно неупругого удара? 11. Выполняется ли закон сохранения механической энергии при движении груза и сваи после удара? 12. Укажите формулу работы постоянной силы. 13. Как работа силы, действующей на тело, связана с изменением механической энергии тела? 14. Как найти силу, с которой свая действует на груз при их абсолютно неупругом ударе? 15. Каким должно быть соотношение между внешней силой F и внутренней f при кратковременном ударе, чтобы приближенно выполнялся закон сохранения импульса? 16. Чему равна величина необратимых потерь механической энергии при ударе груза и сваи? 17. Как меняется доля необратимых потерь механической энергии во время удара груза и сваи при увеличении массы сваи и неизменной массе груза? 18. Нарисуйте эскиз экспериментальной установки 19. Какая система тел является изолированной ? 20. По какой формуле можно найти величину необратимых потерь механической энергии при ударе груза и сваи ? 21. Как определяют высоту Н свободного падения груза до удара? 22. Как вычисляют полуширину доверительного интервала DН высоты свободного падения груза до удара? 23. Как определяют путь S замедленного движения груза и сваи после удара ? 24. Как вычисляют полуширину доверительного интервала DS величины пути замедленного движения груза и сваи после удара ? 25. По какой формуле определяют величину внешней силы F ? 26. Как определяют полуширину доверительного интервала DF внешней силы ? 27. Какая величина определяется в упражнении 2 и по какой формуле ? 28. Как определяют полуширину доверительного интервала Df силы, с которой свая действует на груз? 29. Какая величина определяется в упражнении 3? 30. По какой формуле можно найти долю необратимых потерь механической энергии при ударе груза и сваи? |



 , с которыми на тело с номером i действуют тела, не вошедшие в систему;
, с которыми на тело с номером i действуют тела, не вошедшие в систему; взаимодействия тел системы с номерами i и k. По третьему закону Ньютона :
взаимодействия тел системы с номерами i и k. По третьему закону Ньютона : или
или  . (1)
. (1) .
. записать в виде
записать в виде  ,
, - малое изменение скорости тела за малый промежуток времени Dt, то второй закон Ньютона принимает вид
- малое изменение скорости тела за малый промежуток времени Dt, то второй закон Ньютона принимает вид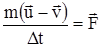 или
или  , (2)
, (2) - начальная скорость тела;
- начальная скорость тела;  - конечная скорость спустя малый промежуток времени Dt. Величина
- конечная скорость спустя малый промежуток времени Dt. Величина  - импульс тела, а
- импульс тела, а  - импульс силы.
- импульс силы. и
и  и на тела действуют внешние силы
и на тела действуют внешние силы  и
и  . Запишем уравнение (2) для каждого тела системы:
. Запишем уравнение (2) для каждого тела системы: ; (3)
; (3) . (4)
. (4) . (5)
. (5) ;
;  ), то суммарный импульс тел такой системы сохраняется, т.е.
), то суммарный импульс тел такой системы сохраняется, т.е. . (6)
. (6) соударяющихся тел может быть достаточно большим, а время удара Dt очень мало (
соударяющихся тел может быть достаточно большим, а время удара Dt очень мало (  с). Поэтому ускорения тел и внутренние или ударные силы
с). Поэтому ускорения тел и внутренние или ударные силы  во время удара могут быть очень большими. Эти силы значительно превосходят внешние силы:
во время удара могут быть очень большими. Эти силы значительно превосходят внешние силы:  . Мерой механического воздействия на тело за время удара является импульс
. Мерой механического воздействия на тело за время удара является импульс  ударной силы
ударной силы  ,
, - средняя ударная сила за время Dt.
- средняя ударная сила за время Dt. ; (3¢)
; (3¢) . (4¢)
. (4¢) . Для такого удара уравнение (6) принимает вид
. Для такого удара уравнение (6) принимает вид .
. . (7)
. (7) В модели копра (см.рис.4) груз 1, падая почти свободно по вертикальной направляющей с некоторой высоты Н, приобретает скорость и совершает абсолютно неупругий удар со сваей 2, которая до удара покоилась.
В модели копра (см.рис.4) груз 1, падая почти свободно по вертикальной направляющей с некоторой высоты Н, приобретает скорость и совершает абсолютно неупругий удар со сваей 2, которая до удара покоилась. , (8)
, (8) . (9)
. (9) является внешней силой. Проекция векторного уравнения (3) на ось координат У, направленную вертикально вверх, имеет вид
является внешней силой. Проекция векторного уравнения (3) на ось координат У, направленную вертикально вверх, имеет вид  .
. . (10)
. (10) . (11)
. (11) . (12)
. (12) падающего груза, то получим долю необратимых потерь механической энергии
падающего груза, то получим долю необратимых потерь механической энергии
 . (13)
. (13) . (13¢)
. (13¢) .
.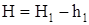 , (14)
, (14)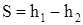 . (15)
. (15) , совершаемая при замедленном движении груза и сваи,
, совершаемая при замедленном движении груза и сваи, (16)
(16) .
. или
или . (17)
. (17)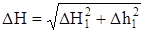 ;
; 
 .
. . (18)
. (18) . (19)
. (19) . (20)
. (20)