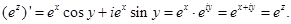ПОЗНАВАТЕЛЬНОЕ
| Предел, непрерывность, производная функции комплексного переменного.
Лекция 11 Тема:Комплексные функции. Предел, непрерывность, производная. Аналитическая функция. Условие Коши-Римана. Комплексные числа в алгебраической и тригонометрической форме и действия над ними. Число z=x+iy, где х и у действительные числа, а Число
Модуль комплексного числа есть расстояние от точки z до начала координат и обозначается |z|,
Действия над комплексными числами в алгебраической форме.
1) Сложение комплексных чисел.
2) Умножение комплексных чисел. Умножение комплексных чисел производится по правилу умножения многочлена на многочлен, учитывая, что
3) Деление комплексных чисел.
Тригонометрическая форма комплексного числа. Пусть z=x+iy.
Рассмотрим полярную систему координат с полюсом в т. О и полярой ОХ. В этом случае формулы перехода от декартовой системы координат к полярной имеют вид:
и комплексное число z запишется в виде z=
Модуль комплексного числа, определяется однозначно: Умножение комплексных чисел в тригонометрической форме.
В частности, Функции комплексного переменного. Определение 1: Говорят, что на множестве Е точек комплексной плоскости z задана функция w=f(z), если по вполне определенному закону каждой точке Множество Е называется множеством определения функции f(z), а множество Q всех значений w, которые принимает f(z) на Е, - множеством ее изменения. Наиболее важным случаем является тот, когда Е и Q являются областями. Если положить z=x+iy, a w=U(x,y)+i Предел, непрерывность, производная функции комплексного переменного. Пусть функция w=f(z) определена и однозначна в некоторой окрестности точки Будем говорить, что предел функции w=f(z) существует при Так как определение предела функции f(z) сводится к определению предела действительных функций, то теоремы о пределе суммы, произведения, частного сохраняются и для функций комплексного переменного. Определение 2: Определение предела функции комплексного переменного можно сформулировать и с помощью понятия окрестности. Число Определение 3: Пусть функция W=f(z) определена в некоторой окрестности точки Отметим, для того, чтобы функция f(z)=U(x,y)+ Так как определение непрерывности функции комплексного переменного аналогично определению непрерывности функции действительного переменного, то теоремы о непрерывности суммы, произведения, частного остаются справедливыми и для функций комплексного переменного. Определение 4: Пусть f(z) определена в некоторой окрестности точки z, включая саму точку z. Производной функции f(z) в точке z называется предел:
В этом случае говорят, что функция f(z) дифференцируема в точке z. Условия дифференцируемости функции f(z)=U(x,y)+ Теорема. (Условия Коши-Римана)(Эйлера-Даламбера). Пусть f(z)=U(x,y)+
Доказательство. Необходимость. Дано: f(z) в точке z имеет производную. Требуется доказать, что выполняются равенства Пусть
Далее, положим, что
Достаточность. Дано Так как U(x,y) и
Далее имеем:
Учитывая условия Коши-Римана, будем иметь:
Так как обычные свойства алгебраических действий и предельного перехода сохраняются при переходе к функциям комплексного переменного, то сохраняются обычные правила дифференцирования.
C учетом условий Коши-Римана, производную f’(z) можно находить по формуле: Определение 5. Функция называется аналитической в области, если она имеет производную в каждой точке этой области. Отметим, что понятие аналитической функции относится только к однозначным функциям, т.к. понятие предела и производной было дано для однозначных функций. Пример 1. Проверить выполнение условий Коши-Римана для функции Решение.
Следовательно,
|
 или
или  , называется комплексным числом в алгебраической форме.
, называется комплексным числом в алгебраической форме. называется действительной частью комплексного числа, а
называется действительной частью комплексного числа, а  - мнимой частью. Комплексное число изображается точкой на комплексной плоскости.
- мнимой частью. Комплексное число изображается точкой на комплексной плоскости.
 . Сопряженным числом для z=x+iy называется число
. Сопряженным числом для z=x+iy называется число  =x-iy.
=x-iy.  .
.

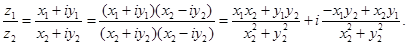

 ,
, +i
+i  =
= 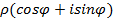 ,
, z=|z|(cos
z=|z|(cos  +isin
+isin  .
. а Argz определен лишь с точностью до любого слагаемого, кратного 2π. Через argz обозначается главное значение Argz, которое является одним из значений Argz.
а Argz определен лишь с точностью до любого слагаемого, кратного 2π. Через argz обозначается главное значение Argz, которое является одним из значений Argz.
 .
. ставится в соответствие точка w или совокупность точек. В первом случае функция называется однозначной, а во втором случае многозначной.
ставится в соответствие точка w или совокупность точек. В первом случае функция называется однозначной, а во втором случае многозначной. (x,y), то задание функции комплексного переменного w=f(z) равносильно заданию двух функций двух переменных U(x,y) и
(x,y), то задание функции комплексного переменного w=f(z) равносильно заданию двух функций двух переменных U(x,y) и  , кроме, быть может самой точки
, кроме, быть может самой точки  .
. , если существуют оба предела
, если существуют оба предела  , при этом будем полагать:
, при этом будем полагать:  .
. называется пределом функции W=f(z) в точке
называется пределом функции W=f(z) в точке  , то
, то  . Отметим, что f(z) стремится к
. Отметим, что f(z) стремится к 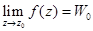 , то при стремлении z к
, то при стремлении z к  .
. (x,y) была непрерывной в точке
(x,y) была непрерывной в точке  .
.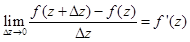
 (условия Коши-Римана).
(условия Коши-Римана). существует, то
существует, то 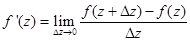 , где
, где 
 , тогда
, тогда  .
.
 =0, тогда
=0, тогда  . Отсюда следует равенство
. Отсюда следует равенство =
= 
 . Так как два комплексных числа равны, то равны соответственно их действительные и мнимые части,
. Так как два комплексных числа равны, то равны соответственно их действительные и мнимые части,  и
и  . Это означает, что выполняются условия Коши-Римана.
. Это означает, что выполняются условия Коши-Римана. существует.
существует. , где
, где 

 +
+  , где
, где  .
.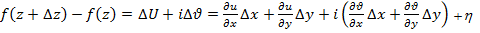 , где
, где 



 , где u=g(z);
, где u=g(z);  , где f(z) и
, где f(z) и  взаимно обратные функции.
взаимно обратные функции. .
. и найти ее производную.
и найти ее производную.


 .
.