 ПОЗНАВАТЕЛЬНОЕ
| Приклади для самостійного розв’язання 12
Множини. Деякі приклади числових множин
Множина – одне з важливіших понять математики, не означається через які-небудь інші елементарні поняття і вводиться аксіоматично. Описати термін множини можна як сукупність, об’єднання, набір деяких об’єктів довільної природи — елементівмножини. Наприклад, множина книг в бібліотеці, множина книг в бібліотеці з даної галузі знань, множина студентів факультету, множина парних чисел, множина точок заданого відрізка і т.п. Як бачимо з прикладів множини можуть бути скінченнимиабо нескінченними. Множини прийнято позначати великими буквами Якщо елемент Множина, що не містить жодного елемента називається порожньою і позначається Розглянемо деякі означення. Означення 1. Дві множини Означення 2. Множина Це позначається так: Наприклад, якщо множина Означення 3. Множина елементів Означення 4. Множина елементів Якщо, наприклад,
Рис.1.
Рис.2. Означення 5. Різницеюмножин
Рис. 3. Задача. Нехай Наведемо приклади відомих множин. Множина натуральних чисел : Множина цілихчисел : Множина раціональнихчисел
Числа, які виражаються нескінченними неперіодичними десятковими дробами називаються ірраціональними. Об’єднання всіх раціональних і ірраціональних чисел утворюють множину Має місце включення Між множиною дійсних чисел та множиною точок числової вісі існує взаємно однозначна відповідність.
Сталі та змінні величини
Величини, які при заданих умовах не змінюють свого значення, називаються сталими. Наприклад, відношення довжини кола до діаметра, як відомо, дорівнює Величини, які в даному процесі набувають різних значень називаються змінними. Наприклад, в процесі руху точки змінними є пройдений точкою шлях, її координати відносно заданої системи координат і т.п. Сталі величини позначають початковими буквами латинського алфавіту Серед змінних величин зручно виділити такі, що набувають окремі ізольовані значення, наприклад, значення натуральних чисел Якщо змінна величина набуває всіх значень з деякого проміжка, то вважають, що вона змінюється неперервно. Наприклад, довжина стовпчика термометра при зміні температури приймає всі значення з деякого відрізка. Нехай Відрізком Напівінтервалами Відрізок, інтервал або напівінтервал ми будемо називати ще проміжком. Проміжки зміни змінної х можуть появлятись, наприклад , при розв’язувані нерівностей, які в свою чергу виникають при дослідженні функції. Приклади. Визначити проміжки зміни змінної х , задані такими нерівностями: 1. 3х + 5>0; 2. х2 ≤ 9; 3. -7 < 5 – 2х ≤ 9 .
Розв’язання. 1. 3х + 5>0
Область розв’язків – проміжок: 2. х2 ≤ 9 Далі нерівність розв’язуємо методом інтервалів, визначаючи знак виразу (х+3)(х-3) в „пробних” точках кожного з інтервалів.
Областю розв’язків є відрізок -3≤х≤3 або х 3. Для розв’язання подвійної нерівності віднімемо із всіх її частин по 5 і розділимо на (-2) (знаки нерівностей при діленні на від’ємне число змінюються на протилежні ) -7-5< 5-2х-5≤ 9-5 -2≤ х< 6, або ж
На рисунках зображення точки повним кружечком означає, що точка включається до даного проміжку, пустим кружечком O - точка не включається. Приклади для самостійного розв’язання Визначити і побудувати на числовій осі проміжки зміни змінної х, задані нерівностями: 1. 4. Відповіді. 1. 4.
12 |



 а їх елементи – малими, наприклад,
а їх елементи – малими, наприклад,  .
. належить множині
належить множині 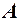 , то пишуть
, то пишуть  , якщо ж елемент
, якщо ж елемент  не належить множині
не належить множині  або
або  .
. .
. називаються рівними (позначають
називаються рівними (позначають 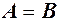 ), якщо вони складаються з однакових елементів.
), якщо вони складаються з однакових елементів. і читається “
і читається “  .
.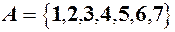 ), а
), а  , то
, то  .
.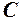 , які належать множині
, які належать множині  .
. і
і 

 , що містить ті елементи
, що містить ті елементи 
 . Знайти:
. Знайти:  .
. .
. .
. – це числа вигляду
– це числа вигляду  , де
, де і
і  – цілі числа,
– цілі числа, 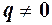 . Нагадаємо, що раціональні числа можуть виражатися десятковими дробами: скінченними або періодичними.
. Нагадаємо, що раціональні числа можуть виражатися десятковими дробами: скінченними або періодичними. дійсних чисел.
дійсних чисел. .
. ; сума внутрішніх кутів трикутника дорівнює
; сума внутрішніх кутів трикутника дорівнює  , чотирикутника —
, чотирикутника —  ; швидкість світла у вакуумі
; швидкість світла у вакуумі  км/с , сталим є прискорення земного тяжіння в даній точці Землі і т.п..
км/с , сталим є прискорення земного тяжіння в даній точці Землі і т.п.. а змінні – останніми буквами
а змінні – останніми буквами  .
. , або значення деякої послідовності, наприклад, арифметичної чи геометричної прогресій. Такі змінні прийнято позначати
, або значення деякої послідовності, наприклад, арифметичної чи геометричної прогресій. Такі змінні прийнято позначати  і називають ще дискретними змінними.
і називають ще дискретними змінними. і
і  – дійсні числа ,
– дійсні числа ,  , їм відповідають точки на числовій осі.
, їм відповідають точки на числовій осі.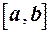 називається множина чисел (точок)
називається множина чисел (точок)  , при цьому пишуть ще
, при цьому пишуть ще  . Інтервалом
. Інтервалом  називається множина чисел
називається множина чисел  . Множину всіх дійсних чисел (точок числової прямої) будемо позначати інтервалом
. Множину всіх дійсних чисел (точок числової прямої) будемо позначати інтервалом  , це означатиме, що для змінної
, це означатиме, що для змінної  . Інтервалом
. Інтервалом  є множина чисел більших від
є множина чисел більших від  . Аналогічно інтервал
. Аналогічно інтервал  означає множину точок
означає множину точок  .
. або
або  називаються множини точок, для яких відповідно
називаються множини точок, для яких відповідно  або
або  .
. >-5
>-5  >
>  або
або 
 <х<
<х<  .
. х2-9 ≤ 0
х2-9 ≤ 0 
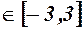 .
. або
або .
.
 2.
2.  3.
3. 

 2.
2.  . 3.
. 3. 
