 ПОЗНАВАТЕЛЬНОЕ
| Метод Гаусса (метод исключения неизвестных) позволяет найти
Примерный перечень вопросов По дисциплине «Высшая математика (1 часть)» 1. Матрицей размера 2. Единичной матрицей второго порядка является матрица (единичная матрица-элементы главной диагонали равны единице, второго порядка n (столбцы) равны 2) 3. Нулевая матрица может быть (когда все её элементы равны нулю) 4. Транспонированная матрица к матрице 5. Матрицы 6. Умножить матрицу на число 7. Матрицы 8. Матрицы 9. При умножении матриц 10. Какая из формул является неверной для умножения матриц: 11. Матрица 12. Обратная матрица для матрицы 13. Матрица 14. Обратная матрица к матрице 15. Какое равенство неверно для обратных матриц: 16. Определитель матрицы вычисляется, только если матрица 17. Определитель второго порядка вычисляется по формуле:
18. Определитель квадратной матрицы 19. Если элементы строк или столбцов определителя пропорциональны, то определитель равен (нулю) 20. При замене всех строк определителя соответствующими столбцами определитель ( не изменится) 21. Определитель Метод Гаусса (метод исключения неизвестных) позволяет найти 23. Однородная система линейных алгебраических уравнений 24. Система линейных алгебраических уравнений совместна, если 25. Величина, которая определяется только числовым значением, называется: 26. На плоскости вектор изображается 27. Единичным вектором называется вектор, имеющий 28. Векторы называются коллинеарными, если 29. Векторы называются компланарными, если 30. Линейными операциями над векторами называются 31. Сумму двух векторов на плоскости можно найти по 32. Вектор 33. Упорядоченная система трёх векторов называется базисом, если 34. Базис векторов называется ортонормированным, если 35. Скалярным произведением двух векторов 36. Скалярный квадрат вектора равен 37. Если векторы 38. Если скалярное произведение двух векторов равно 0, то вектора 39. Длина вектора 40. Даны векторы 41. Векторным произведением двух векторов называется 42. Векторное произведение векторов 43. Если смешанное произведение векторов, 44. Смешанное произведение векторов 45. Уравнение прямой на плоскости, заданной точкой и нормальным вектором имеет вид: 46. Общее уравнение прямой на плоскости имеет вид 47. Уравнение прямой с угловым коэффициентом имеет вид 48. Каноническое уравнение прямой на плоскости имеет вид 49. Уравнение прямой на плоскости, проходящей через две точки, имеет вид 50. Числа 51. Числа 52. Числа 53. Прямая 54. Прямые 55. Уравнение плоскости, заданной точкой и нормальным вектором, имеет вид 56. Числа 57. Областью определения функции 58. Какая из приведенных функций не является элементарной: 59. Какая из приведенных функций является ограниченной: 60. Бесконечно малой последовательностью называется последовательность, имеющая предел, равный: 61. Последовательность называется сходящейся, если она: 62. Пятый член последовательности 63. Функция 64. Числом е называется предел: 65. Предел 66. Производная постоянной равна: 67. Производная функции 68. Производная частного двух дифференцируемых функций 69. Правило Лопиталя состоит в следующем: если 70. Операция нахождения производной функции 71. Если функция 72. Если при переходе через критическую точку Примерные тестовые задания по Высшей математике (1 часть) (правильные ответы отмечены «+») |



 называется (прямоугольная таблица чисел, содержащая m строк и n столбцов)
называется (прямоугольная таблица чисел, содержащая m строк и n столбцов) содержит всегда( строки и столбцы меняются местами ,если матрица А имеет размер n x m, то транспонированная матрица АТ имеет размер m x n)
содержит всегда( строки и столбцы меняются местами ,если матрица А имеет размер n x m, то транспонированная матрица АТ имеет размер m x n) можно складывать, если только( матрицы являются одноразмерными)
можно складывать, если только( матрицы являются одноразмерными) означает( умножить каждый элемент заданной матрицы на это число)
означает( умножить каждый элемент заданной матрицы на это число) называются согласованными, если только( количество столбцов матрицы А равно количеству строк матрицы В)
называются согласованными, если только( количество столбцов матрицы А равно количеству строк матрицы В) называется обратной к матрице
называется обратной к матрице 

 равен (3)
равен (3)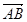 задан координатами точек
задан координатами точек  и
и  называются
называются вычисляется по формуле
вычисляется по формуле ,
,  . Тогда их скалярное произведение вычисляется по формуле
. Тогда их скалярное произведение вычисляется по формуле , равно 0, то они
, равно 0, то они вычисляется по формуле
вычисляется по формуле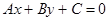 это
это и
и  , взятые по модулю, в уравнении прямой
, взятые по модулю, в уравнении прямой  , это
, это ,
,  в уравнении прямой
в уравнении прямой  , это
, это ,
,  ,
,  проходит
проходит ,
,  параллельны, если
параллельны, если в уравнении плоскости
в уравнении плоскости  это
это является промежуток:
является промежуток: равен:
равен: называется бесконечно большой функцией при
называется бесконечно большой функцией при  , если:
, если: равен:
равен: равна:
равна: и
и  определяется по формуле:
определяется по формуле: или
или  , то:
, то: называется:
называется: и
и  для любого
для любого  , то на этом интервале функция:
, то на этом интервале функция: меняет знак с “+” на “–“, то
меняет знак с “+” на “–“, то