 ПОЗНАВАТЕЛЬНОЕ
| Геометрические приложения производной (№№ 29-31)
Начала математического анализа Часть 2: «Приложения производной» Раздел 1 (базовый уровень максимальная оценка – «удовлетворительно») Геометрические приложения производной (№№ 1-7) 1. Прямая 2. Написать уравнения касательной, проведённой к кривой y=e 3. Какой угол с положительным направлением оси OX составляет касательная, проведённая к графику функции f(x) = 4. Составьте уравнения касательных к графику функции f(x) = x3 + x2, угловые коэффициенты которых равны 8. 5. На рисунке изображен график производной функции
6. На рисунке изображен график производной функции
7. На рисунке изображён график функции
Физические приложения производной (№№ 8-16). 8. Движение точки, движущейся прямолинейно, задано уравнением s = t3 + 5t2 + 4. Найдите скорость и ускорение в момент t = 2с 9. Точка движется прямолинейно по закону s = 6t – t2. В какой момент времени скорость точки окажется равной нулю? 10. Закон изменения температуры Т тела в зависимости от времени t задан уравнением Т = 0,2t2. С какой скоростью нагревается это тело в момент времени t = 10? 11. Тело массой 10 кг. движется прямолинейно по закону s = 3t3 + t + 4. Найти кинетическую энергию тела (mv2/2) через 4с после начала движения. 12. Сила тока I изменяется в зависимости от времени t по закону I=0,4t2 (I - в амперах, t - в секундах). Найдите скорость изменения силы тока в конце 8-ой секунды. 13. Тело вращается вокруг оси, причём закон изменения угла j = 0,1t2. Найти угловую скорость вращения тела в момент t = 5. 14. С крыши дома, имеющего высоту равную 50 м брошен вертикально вверх мяч со скоростью 20м/сек. Найти: а) скорость подъёма в конце второй секунды; б) момент начала падения в) наибольшую высоту подъёма относительно поверхности земли. 15. Найти силу F, действующую на материальную точку массы « m », которая движется прямолинейно по закону S = 2t3 - t2 при t = 3c. . 16. Известны уравнения движения двух точек: S1 = 2t3 – 4t2 + 5t и S2 = 2t3 – 1,5t2. Найдите ускорение движущихся точек в тот момент, когда их скорости равны.
Применение производной к исследованию функций Найдите наименьшее значение Y=f(X) функции на отрезке [X1;X2] (№№ 17-18)
Найдите наибольшее значение Y=f(X) функции на отрезке [X1;X2] (№№ 19-20)
Исследовать функции на экстремумы (№№ 21-24):
Исследовать функцию и построить ее график (№№ 25-28).
Раздел 2 (базовый уровень, максимальная оценка – «отлично») Геометрические приложения производной (№№ 29-31) 29. Найдите общую точку касательных к графику y = x2 – 3x + 2, одна из которых касается графика в точке с абсциссой x = 2, а другая – в точке с абсциссой x = 1. 30. Дана парабола y = x2 – 2x + 7. Составьте уравнение касательной, перпендикулярной прямой, проходящей через начало координат и вершину параболы.
31. Составьте уравнение касательной к кривой xy = 2 в точке N(2;1)
Физические приложения производной (№№ 32-33).
32. Зависимость между количеством
Исследовать функции на экстремумы (№№ 33-35):
Найти асимптоты графиков функции (№№ 36-41):
Исследовать функцию и построить ее график (№№ 42-47)
|



 параллельна касательной к графику функции
параллельна касательной к графику функции 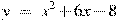 . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания. в точке её пересечения с осью oy.
в точке её пересечения с осью oy. в точке с абсциссой x = -
в точке с абсциссой x = - 
 , определенной на интервале
, определенной на интервале  . В какой точке отрезка
. В какой точке отрезка 

 . Найдите количество точек минимума функции
. Найдите количество точек минимума функции  .
.
 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции 
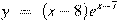 ,
, 
 ,
, 
 ,
, 






 ;
;

 вещества, полученного в некоторой химической реакции, и временем t выражается уравнением x = A(1-e-kt). Определить скорость реакции.
вещества, полученного в некоторой химической реакции, и временем t выражается уравнением x = A(1-e-kt). Определить скорость реакции.










 ;
;
